49. Теплоемкость многоатомных газов.

Ч ислом степеней свободы i- назыв-ся число независимых параметров координат, характеризующих состояние системы. Молекулу одноатомного газа можно рассматривать как материальную точку, положение которой хар-ся тремя координатами: одноатомный газ (He) : i=3 (x,y.z). Молекулы двухатомного газа(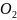 ) можнр рассматрив. как систему 2-ух материальных точек с жесткой связью.

Трехатомный газ (C

i = 3+3+3-1-1-1=6

Е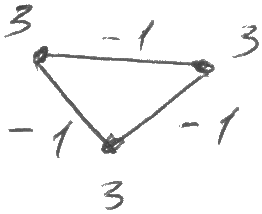 сли связи молекул нежесткие, то необходимо учитывать и колебательн. степени свободы. Число степеней свободы i равно сумме чисел степеней свободы поступательного движения, вращательн. Движения и удвоенного числа степеней колебательного движения:

i=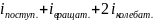

Средняя кинетич. энергия идеального одноатомного газа с числом степеней свободы i=3 равна:

Т.к. все степени свободы равноправны, то на одну степень свободы приходится энергия= . Тогда приходим к закону о равном распределении энергии по степеням свободы. Для системы в термодин. Равновесии на каждую степень свободы приходится Е= Тогда для молекулы многоатомного газа с числом степени свободы i: Е=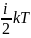

Найдем внутрен. энергию одного моля идеалього газа:

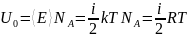
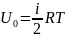; ; U= RT

Теплоемкость тела - кол-во теплоты, которую надо сообщить телу, чтобы нагреть его на 1 К (кельвин)

Молярная теплоемкость-кол-во теплоты, которую надо сообщить или отнять от одного моля в-ва, чтобы нагреть или охладить его на 1К. ) ; [C]=

Удельная теплоемкость- кол-во теплоты, которую надо сообщить 1кг в-ва, чтобы нагреть его на 1К. [

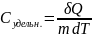δQ= ; Q=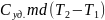

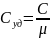
Теплоемкость в-ва зависит от вида протекающего процесса. В газе различают теплоемкость при постоянном объеме и постоянном давлении. (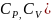

δQ=dU+pdV;

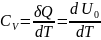
ν=1, V=const, dV=0 ; d ;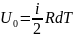

;

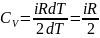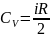
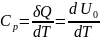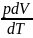+ ; pV=RT

p=const; pdV=RdT

;

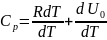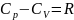- ф-ла Майера

- показатель адиабаты.

Мы рассмотрели классическую теорию теплоемкости: теплоемкости не зависят от температуры. Однако при низких температ. важную роль начинают играть квантовые эффекты (происходит замораживание вращат. и колебат. степней свободы и появляется зависимость теплоемкости от температуры).

50. Применение I начала термодинамики к изопроцессам(термодинамическим процессам).

Изопоцесс – термодинамич. проц.,при кот. один из параметров остается постоянным.

T=const – изотермическ., p=const – изобарн.,

V = const – изохорн.,

δQ = const – изэнтропический

1) T = const

δQ = dU+δA ; dU = 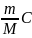_VdT = 0

δQ= δA все тепло,сообщенное сист. в изотермическом проц. идет на работу

δ A=pdV

p= ; δA=

Проинтегрируем обе части ур-я от сост. V₁ к V₂

A₁₂=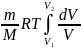 ; A₁₂=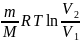

2) p=const

δQ=dU+ pdV тепло сообщ. сист. в изобарн. проц. идет на измен. внутрен. энергии и на работу сист.

Работа в изобарном проц.:

δA=pdV

A₁₂=p ; A₁₂=p(V₂-V₁) ; A₁₂=p∆V

d|| pV= возьмем дифференциал

pdV=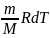 ; δA=

Проинтегрируем:

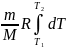A = ; A = 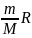(T₂-T₁) ; A = ∆T

ν = 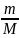= 1моль

R = физический смысл: универсальная газовая постоян. R численно равна работе 1 моля идеального газа при изобарном нагревании его на 1 К.

3) V=const

δQ=dU

δA=pdV=0 тепло сообщ. сист. в изохорн. проц. идет на увелич. внутр. энерг. сист.