
- •1О. Кинематика поступательного движения.
- •2О. Кинематика вращательного движения.
- •3О. Динамика частиц. Закон ньютона.
- •4О. Неинерциальные системы отсчета (нсо). Силы инерции.
- •5О. Основное ур-ние динамики вращательного движения тв. Тела.
- •7О. Закон сохранения импульса.
- •8О. Работа.Мощность.Кинетическая энергия системы.
- •9О. Потенциальная энергия системы.
- •10. Закон сохранения энергии в механике
- •11О. Закон сохранения момента импульса.
- •12О. Движение тела переменной массы.
- •13О. Кинематика гарманических колебаний
- •14О. Гармонический осциллятор.
- •15О. Примеры гармонических осцилляторов.
- •16. Сложение гармонических колебаний одного направления и частоты.
- •17. Сложение взаимно перпендикулярных гармонических колебаний.
- •18. Затухающие колебания.
- •19.Вынужденные колебания. Резонанс.
- •20.Упругие волны в средах.
- •21О.Бегущие волны. Фазовая скорость. Длина волны. Волновое число.
- •22. Одномерное волновое ур-е. Энергия волны.
- •23. Распространение волн в средах с дисперсией. Групповая скорость, ее связь с фазовой скоростью.
- •24. Стоячие волны
- •25. Элементы акустики.
- •26.Модуль Юнга. Скорость звука.
- •28. Постулаты сто. Преобразование
- •29. Средства преобразования Лоренца.
- •30. Релятивистский закон сложения скоростей.
- •31. Интервал между событиями и его инвариантность в преобразовании Лоренца
- •32. Релятивистская динамика, кинетическая энергия сто.
- •33. Связь массы, энергии, импульса в сто
- •34О. Эффект Доплера
- •35О. Принцип эквиваленности.Понятие о ото
- •36О. Равновесие и течение жидкости и газа
- •37О. Уравнение неразрывности струи. Уравнение Бернулли
- •38. Уравнение Эйлера. Движение идеальной жидкости.
- •39. Течение вязкой жидкости. Формула Стокса.
- •40. Течение вязкой жидкости в трубах. Формула Пуазейля.
- •41. Динамический и статистический закономерности в физике.
- •42. Уравнение состояния идеального газа.
- •43. Основное уравнение молекулярно-кинетической теории газов (мкт).
- •44. Молекулярно-кинетический смысл абсолютной температуры.
- •45. Распределение Максвелла.
- •46. Параметрическая формула распределения Больцмана.
- •47. Распределение Гиббса.
- •48. Первое начало термодинамики.
- •49. Теплоемкость многоатомных газов.
- •50. Применение I начала термодинамики к изопроцессам(термодинамическим процессам).
- •51. Адиабатический процесс.
- •52. Политропный процесс
- •53. Теплоемкость и работа газа в политропном процессе
- •54. Обратимые и необратимые процессы, круговой процесс, тепловые двигатели, холодильные машины.
- •55. Цикл Карно. Максимальный кпд тепловой машины.
- •56. Технические циклы.
- •57. Второе начало термодинамики (6 формулировок).
- •58. Энтропия
- •59.Принцип возрастания энтропии
- •60. Определение энтропии неравновесной системы через статистический вес состояния. III начало термодинамики.
- •61. Метод термодинамических потенциалов (характеристических функций).
- •62. Явления переноса. Средняя длина свободного пробега молекул.
- •63. Коэффициент диффузии.
- •64. Теплопроводность. Коэффициент теплопроводности.
- •65. Уравнение теплопроводности.
- •66. Вязкость. Коэффициент вязкости.
- •67. Фазовые равновесия и превращения. Фазы и фазовые превращения.
- •68. Уравнение Клайперона - Клаузиса.
- •69. Реальные газы. Уравнение Ван – дер - Вальса .
- •70. Изотермы Ван-дер-Ваальса. Критич. Состояние. Внутр. Энергия реального газа.
- •71. Твёрдые тела.Теплоёмкость кристалла
- •72. Жидкости.Поверхн. Натяж. Жидк.
- •73. Смачивание и капиллярные явления
- •74. Принцип динамич. Отопления
- •75. Элементы физики полимеров
- •1О. Кинематика поступательного движения.
46. Параметрическая формула распределения Больцмана.
Получим законы изменения давления p газа. С высотой h в однородном поле тяжести земли при постоян. температ.(g=const, T=const)
Р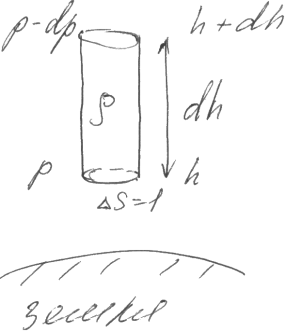 ассм.
вертикальный цилиндр в поле тяжести
земли.
ассм.
вертикальный цилиндр в поле тяжести
земли.
Разность давлений на высоте h, dh = весу газа в искомом цилиндре.
(p-dp) – p = ρgdhΔS, ΔS=1
-dp = ρgdh
PV=
 ; m = ρV; P =
; m = ρV; P =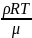 ;
;
ρ= ; dp=
; dp= ;
;
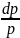 =
-
=
-
 ;
логарифмируем
;
логарифмируем
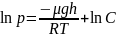 ; потенцируем
; потенцируем
P=C
Пусть
при h=0,
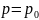 ,
C=
,
C=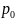
p
=

μ
=
 ;
;
 =
=
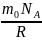 =
=
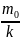 ;
;
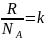
p
=
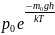 ; p = nkT ;
=
; p = nkT ;
=
n
=
 ;
;

n= – распределение Больцмана
– распределение Больцмана
47. Распределение Гиббса.
Рассмотр.
систему из N частиц и пусть система
подчиняется законом Ньютоновской
механики: положение каждой частицы
можно характери-зовать к-тами x,y,z и
проекциями импульса
 ,
,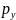 ,
, .
Поэтому можно ввести понятие шестимерного
пространства с ортогональными
(перпендикул.) осями. Состояние N частиц
характер-ся 6N обобщенными координатвми.
Эти координаты записываются в 6N-мерном
пространстве. Пространство 6N с ортогональн.
осями назыв-ся фазовым пространством.
Каждому состоянию системы соответствует
точка в 6N-мерном пр-ве. Задание точки в
этом пространстве означает задание
всех координат и проекций импульса всех
частиц системы. Разобъем фазовое
пространство на 6N-мерные элементарные
ячейки с объемами dqdp,
где
.
Поэтому можно ввести понятие шестимерного
пространства с ортогональными
(перпендикул.) осями. Состояние N частиц
характер-ся 6N обобщенными координатвми.
Эти координаты записываются в 6N-мерном
пространстве. Пространство 6N с ортогональн.
осями назыв-ся фазовым пространством.
Каждому состоянию системы соответствует
точка в 6N-мерном пр-ве. Задание точки в
этом пространстве означает задание
всех координат и проекций импульса всех
частиц системы. Разобъем фазовое
пространство на 6N-мерные элементарные
ячейки с объемами dqdp,
где


dq-совокупность координат всех частиц , dp-совокупность всех проекций импульсов

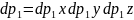
Состояние системы можно храктер-вать с помощью функции распределения:
F(q,p)dqdp=dW
Эта функция распределения задает вероятность того, что точка находится в состоянии , при котором её координаты и импульсы заключены в пределах q, q+dq ; p,p+dp
Эта функция распределения нормирована на1-это означает достоверное событие.
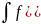 p)dqqp=1
p)dqqp=1
Для
классической системы, находящейся в
равновесии с термостатом, при температуре
Т функция f(q,p) описывается каноническим
распределением Гиббса: f(q,p)=A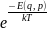
A- постоянная, определ. из условия нормрования ; Е(q,p)-полная энергия системы. Термостатом наз-ся система с бесконечной теплоемкостью. Распределение Гиббса позволяет описывать состояние любой статистической системы: 1) положение энергии, средняя энергия классической системы:

2)
среднее значение энтропии:
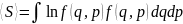
48. Первое начало термодинамики.
В основе термодинамики лежит 4 начала. 0) Нулевое начало термод. устанавлив. Существование температуры(Т). Экспериментально установлен закон теплового равновесия: «если две системы А, В находятся в тепловом равновесии поразнь с С, то система наход. В тепловом равновесии. Разность температур определ. меру отклонения тел от состояния теплового равновесия друг с другом».
1)Первое начало термод.: закон сохранения энергии для термодинам. систем. Внутренняя энергия термодин. систмы(U)- это полная энергия системы, за исключением 1) кинетич. энергии с-мы; 2)потенциальн. энергии с-мы во внешнем поле. Во внутрен. энергию с-мы входят : 1) кинетич. энергия теплового, поступатльн., вращательн. движения молекул газа, частиц. 2) потенциальн. энергия взаимод-вия молекул газа, частиц. 3)энергия электромагнитного излучения с-мы. 4)энергия электронных оболочек. 5) внутрен. энергия. 6) квантовая энерг.
Внутрен.
энергия с-мы одназначно определ-ся
термодинамич. параметрами с-мы. U=f(P,V,T).
Внутр.энергия идеального газа, молекулы
которого не взаимод. на расстоянии- есть
аддитивная ф-ция, т.е. внутрен. энергия
с-мы равна сумме внутрен. энергий
отдельных частиц с-мы. U= .
Существ. 2 основных способа изменен.
внутрен. энергии : 1) путем совершения
работы
.
Существ. 2 основных способа изменен.
внутрен. энергии : 1) путем совершения
работы
 над системой; 2)Путем передачи некоторого
кол-ва тепла δА с-ме. Кол-во работы и
теплоты могут быть эквивалентны, но
качественно они различны. Теплота-это
микроспособ передачи энергии системе
при тепловом контакте системы с внешними
телами.
над системой; 2)Путем передачи некоторого
кол-ва тепла δА с-ме. Кол-во работы и
теплоты могут быть эквивалентны, но
качественно они различны. Теплота-это
микроспособ передачи энергии системе
при тепловом контакте системы с внешними
телами.
3 типа теплообмена: 1)теплопроводность; 2)конвекция; 3)излучение
Работа- микроскопический способ передачи энергии с-мы, когда меняются внешние параметры с-мы.
Количество тепла δQ, сообщаемое системе расходуется на изменение внутрн. энергии с-мы dU и на совершение системой работы над вешними телами δА.
δQ=dU+δA -1-ое начало термодин.
dU
означат, что внутрен. энергия системы-
есть полный дифференциал, т.е. при
совершении системой кругового процесса,
после которого система возвращается в
исходное положение, полное изменение
внутрен. энергии =0, т.е.

К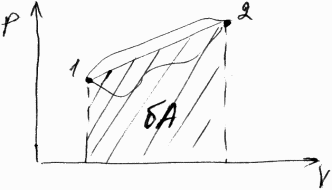 ол-во
теплоты δQ и кол-во работы δА не явл-ся
полными дифференциалами, а они есть
функции процесса, т.е. зависят от способа,
в котором с-ма пришла в исходное
термодинамич. состояние.
ол-во
теплоты δQ и кол-во работы δА не явл-ся
полными дифференциалами, а они есть
функции процесса, т.е. зависят от способа,
в котором с-ма пришла в исходное
термодинамич. состояние.
Интегрируя 1-ое начало для бесконечно малых величин получаем 1-ое начало для конечных измерений:
Q=(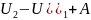
Если
с-ма совершает круговой процесс, то
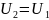 и Q=A
и Q=A
2)Из Q=A вытекает, что невозможно построить периодически действующий двигатель, который каждый раз совершал бы большую работу, чем кол-во сообщаемой ему из вне теплоты.(вечный двигатель 1-ого рода)
3 )Невозможен
тепловой двигатель, у которого КПД>1
)Невозможен
тепловой двигатель, у которого КПД>1
Работа газа при изменении V:
Пусть газ передвигает поршень на величину dx. Тогда работа газа δA=Fdx; F=PS; δA=PSdx; δA=PdV -работа газа.
1)Работа газа положит-на, если объем увеличив-ся, т.е. δQ>0, если dV>0; 2)Работа отрицательна, если объем уменьшается.
δQ=dU+PdV - І начало термодин.
Е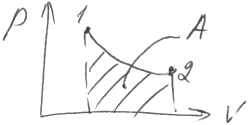 сли
газ переходит из начального состояния
в конечное, то работа представляет собой
интеграл: A=
сли
газ переходит из начального состояния
в конечное, то работа представляет собой
интеграл: A=
На графике такая работа числено равна площади фигуры:
Тепло δQ сообщ-мое системе: δQ > 0, тепло отдоваемое системой: δQ <0.
