44. Молекулярно-кинетический смысл абсолютной температуры.

Сравним уравнение К-М с основным уравнением МКТ:

PV= νRT ν=1 ν=m/M

P=(2/3)n<E> n=Na/V_o P=(2/3) (Na/V_o) <E>

P=RT/V_o, где V_o – молярный объем

<E>=(3/2)(R/Na)T

Постоянная Больцмана называется универсальная газовая постоянная, отнесенная к 1 молекуле.

k=R/Na=1,38 10^-23 Дж/К

<E>=3/2kТ

Абсол темпер ид газа пропорциональна средней кинетической энергии поступательного движения молекул газа: P = nkT.

45. Распределение Максвелла.

Из опыта следует, что газ, заключенный в изолированный сосуд, в отсутствии внешних воздействий (полей) со временем прихода в равновесное стационарное состояние. Распределение максвелла задает распределение молекул по скоростям. Механизм установления такого распределения – это бесчисленные столкновения молекул газа между собой. В силу хаотического движения молекул все направления скорости молекул равномерны, т.е по всем направлениям в среднем движется одинаковое число молекул, тогда распределение скорости одинаково.

Получим вид функций распределенных молекул для модуля скоростей. Выражение f(v)dv дает вероятность того, что скорость наугад выбранной молекулы лежит в пределах (v;v+dv). Выражение f(v)dv дает долю молекул dN(v)dv/N от их общего числа, скорости кот-ых заключены в пределы (v;v+dv)

Пусть φ(v_x)dv_x есть вероятность того, что х-овая компонента скорости молекул лежит в пределах (v_x; v_x+dv_x). Эту вероятность можно представить f(v)dv_xdv_ydv_z где f(v) = φ(v_x)* *φ(v_y) *φ(v_z) - Т.к отриц и положительные компоненты скоростей равноправны, то φ(v_x)=φ(-v_x) тогда функция φ зависит только от модуля скорости или от квадрата скорости, тогда удобней взять вместо квадрата скоростей их кинетические энергии

E_x=1/2 m_ov_x² , E_{у ,} E_z

Тогда мы получаем φ(E_x)φ(E_y)φ(E_z)=f(E_x+E_y+E_z)

Найдём реш последнего функционального ур-ия: пусть E_z = const, тогда: E_x+ E_у= const

φ(E_x)φ(E_y) = const, прологорифмируем:

lnφ(E_x) + lnφ(E_y) = lnconst, продифф-ем:

φ’(E_x)/φ(E_x) + φ’(E_y)/ φ(E_y) = 0

E_x+ E_у= const → dE_x+ dE_у= 0

dφ(E_x)/φ(E_x) = dφ(E_y)/ φ(E_y)

Т.к Е_x и Е_у независимые компоненты то последние соотношение возможно, если:

dφ(E_x)/φ(E_x)=dφ(E_y)/φ(E_y)= - ά – определен в сравнении с основным уравнением МКТ.

ά = 1/Kt φ(E_x)φ(E_y)φ(E_z)=A₁³ e^-άEx

A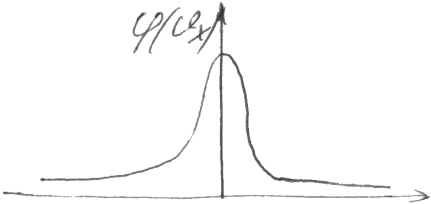 ₁ – получаем из условия нормировки:

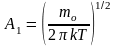
Функция распределения φ(v_x). Такого рода функции, возникающие в теории ошибок, называются распределением гаусса. Оно возникает когда при измерении физ. величины действует множество малых по величине факторов. С учётом распределения можно получить ф-цию распределения: f(v)dv → dv_xdv_ydv_z = 4πυ² dυ

4πυdυ*υ

О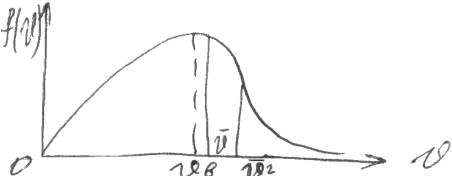 кончательно распределение Максвелла имеет вид:

f(v)= (4/ π^1/2)( m_o/2kT)^3/2 v²e^-mv2/2kT

Очевидно это распределение:

υ→0 f(v) →0 υ→∞ f(v) →0

v_в - вероятностная

v_в = (2kT/ m_o)^1/2=(2RT/ μ)^1/2

С редняя арифметическая скорость молекулы: (<v>)^1/2=(8kT/πm_o)^1/2 =(8RT/πμ)^1/2

k/m_o = R/N_Am_o = R/μ

Средняя квадратическая скорость:

(<v>²)^1/2=(3kT/m_o)^1/2=(3RT/ μ)^1/2

Р ассмотрим распределение максвелла при различной температуре с ростом Т с фор-лы для V_в следует что максимум смещения вправо а величина максимума будет убывать.

З-н Максвелла для безразмерной скорости u = v/ v_в ; f(u)=(4/ π^1/2)u²e^-u2

Распределение Максвелла было проверено эксперементально в 1920 в опыте Штейнера.