37О. Уравнение неразрывности струи. Уравнение Бернулли

Р ассм. сужающуюся струю (трубку тока)

Пусть 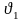частиц жидкости в сечении , а в сечении скорость .

Через сечение за 1 сек пройдёт V жидкости = V₁, через сеч. объёмом: , по заон сохранения масс имеем ,

= , жидкость слабосжимаемая.

,

Произведение скорости несжимаемой жидкости на поперечное сечение трубки, есть величина постоянная для данной трубки. Приходим к уравнению неразрывной несжимаемой жидкости: секундный объёмный (массовый) расход несжимаемой жидкости постоянен вдоль трубки тока. Из сказанного вытекает, что в местах , где трубка уже жидкость течёт быстрее, а где шире –течёт медленнее.

Получим уравнение Бернулли:

Р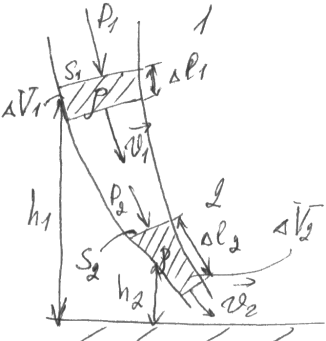 ассм. малый объём жидкости в положении 1

Через время t этот объём перейдёт в положение

В силу равнения неразрывности:

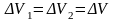
Энергия каждой частицы жидкости складывается из кинетической и потенциальной:

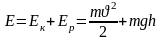
Масса объёмов 1 и 2 :

Тогда при перемещении объёмов жидкости из положения 1 в положение 2 приращение полной механической энергии будет =:

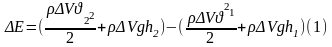
Т.к. жидкость идеальная (нет трения), то приращение энергий объёмов жидкости = разности работ сил давления, приложенных к сечениям и , при этом силы давления на боковые поверхности перпендикулярно перемещению и работы не совершают, имеем:

В силу закона сохранения:

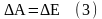
Приравняем (1) и (2), сокращая на ур-ние Бернулли:

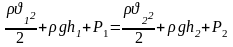
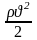-динамическое давление или скоростной напор – дельная кинетическая энергия(энергия на единицу объёма)

-гидростатическое давление или гидравлический напор - дельная потенц. энергия в поле тяжести.

P- статическое давление, т.е. удельная энергия сил давления жидкости

Па=

П олный напор движущейся жидкости складывается из статического, гидравлического и скоростного напоров и остаётся постоянным при движении(g=0).

Из последнего выражения вытекает: «Там, где больше скорость потока, происходит уменьшение статического давления».

38. Уравнение Эйлера. Движение идеальной жидкости.

Рассмотрим движение идеальной жидкости(без внутреннего трения, вязкости). Силы, действующие на объем жидкости, делятся на массовые и поверхностные.

О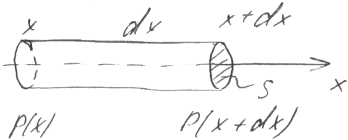 бъемная сила пропорциональна объему dV: f^.dV, где F – объемная плотность массовых сил. Поверхностные силы для идеальной жидкости сводится к силам нормального давления. Касательных сил давления для идеальной жидкости нет. Найдем выражение для силы нормального давления:

Рассмотрим эл-т жидкости в виде цилиндра, расположенного вдоль оси Х с длиной dX, площадью поп.сечения S, и объемом dV=SdX

P(x) и P(x+dx) давление на основание цилиндра.

Проекция сил давления на ось X равна

((p(x)-p(x+dx))S = -dPS = (-dP/dx)(dxS/dv) =

= (- ∂P/∂X)dV

Совершенно аналогично получим выражение для других сил давления по у и z.

Выражение для сил давления

▼= (∂/∂x)i+(∂/∂y)j+(∂/∂z)k (▼- набла)

-gradP=-▼P

По 2з.Ньютона с учетом объемных и поверхностных сил имеем уравнение движения в векторной форме:

dm*dv/dt=fdV-gradPdV=-gradpdV

Ур-е Эйлера в векторной форме:

ρdv/dt=f-gradP (v-вектор)

dv/dt- полное ускорение эл-та жидкости, определяющее изменение скорости рассмотренного эл-та среды. При его перемещении в пространстве т.е. dv/dt=∂v/∂t+(▼v)v

∂v/∂t - локальное ускорение, т.е. какой-либо фиксированной точки пространства.

(▼v)v- конвективное ускорение – характеризует изменения скорости при перемещении эл-та жидкости от точки к точке.

▼v=v_x ∂/∂x + v_y ∂/∂y + v_z ∂/∂z

В проекции на декартовую систему координат предыдущее ур-е примет вид системы из OX, OY, OZ(**):

OX: ∂v_x/∂t +v_x*∂v_x/∂x +v_у*∂v_x/∂y+v_z*∂v_x/∂z)= =(1/ρ)f_x – (1/ρ) ∂p/∂x

OY: - OZ: -

К уравнению (**) надо добавить уравнение неразрывности, которое имеет вид

∂ρ/∂t+ div(ρv(вектор)=0

Если жидкость незжимаема, т.е. ρ=const, то уравнение неразрывности имеет вид:

∂v_x/∂x+ ∂v_y/∂y+ ∂v_z/∂z=0

К искомым уравнениям добавляем основное термодинамическое тождество

TdS=dU+PdV

T- абсол. темп

S- энтропия ; U- внутр. энерг.

P- давление ; V- объем

PdV- работа

Если движущая сплошная среда вязкая, то к силам давления и обьемной силе надо добывить силу вязкости, которая имеет вид: ή^. Δv(скорость)

ή – коэф. Вязкости

Δ – оператор Лапласа ή Δv

Уравнение течения вязкой жидкости ( Ур-е Навье-Стокса) имеет вид

ρdv/dt=f – gradP + ή Δv

Пусть идеальная жидкость покоится dv/dt=0

Основное Уре гидростатики f=grad P

Ускорение равновесия жидкости в поле тяжести: ∂p/∂z = -ρg