30. Релятивистский закон сложения скоростей.

Рассм. движение т.М в системах S и S^’ (υ = const): Пусть в сист.S будет момент врем. t, корд. т.М: , а скорости:

U_x= , U_y= , U_Z=

Пусть в сист.S^’ будет момент врем. t ’, корд. т.М: , а скорости:

= , = , =

Найдём связь скоростей т.М в S и S^’

В силу преобразований Лоренца имеем

=

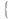
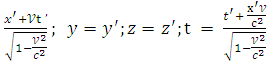
Возьмём полный дифференциал от обеих частей последних равенств:

=

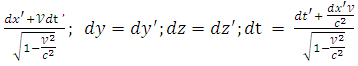
Из последнего в первых трёх формулах поделим соответственно левую и праву части на 4-ю формулу (получим систему):

; ;

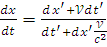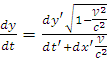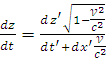
Поделим числитель и знаменатель:

; ;

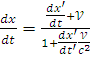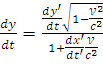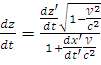
С учётом обозначений скоростей т.М в S и получаем закон преобразования релятивистских скоростей:

; ; (*)

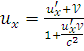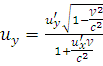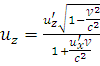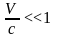, то получаем: U_X = U_X’ + V - теорема о сложении скоростей в классической механике.

Из (*) → ск-ти, большие релятив.скоростей, не могут получаться.

Фотон движ.со скор.

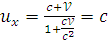
31. Интервал между событиями и его инвариантность в преобразовании Лоренца

Событие - совокупность коорд. (x, y, z, t).

Введём 4-рёхмерное пространство Минковского. В качестве взаимно перпендикулярных осей берут 3 пространственные оси, а 4-я – временная ось. В таком пространстве событие изображается мировой точкой в 4-рёхмерном пространстве. Всякой частице, даже неподвижной, соотв. мировая линия в 4-рёхмерном простр-ве.

Для неподв. т-ки мировая линия – прямая, парал. оси врем. T

В 3-мерном пр-ве: ∆ =

В 4-мерном пр-ве: квадрат расст. между 2 мировыми т-ками с коорд.

( ) и ( ) записыв. в виде квадрата интервала: (1)

Пространство, в котором кв-т расст. определ-ся интерв. , назыв-ся псевдоэвклидовым.

Покажем, что кв-т интервала инвариантен отн. преобразований Лоренца, т.е. он не меняется при перех. от одной инерц. системы отсчёта к другой: Выраж-е (1) – интервал в с-ме S.

В с-ме (2)

В силу преобразований Лоренца

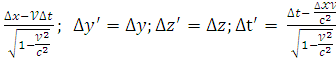( = ) (*)) подставляем (*) в (2) и получаем

Э

тот интервал не меняется, т.к. ∆S инвариантен при переходе от в S. Т.о. он носит абсолный характер. В этой инвариантности проявляется взаимосвязь пространства и врем.

32. Релятивистская динамика, кинетическая энергия сто.

Из постулата теории относит-ти можно показать, что масса тела с увелич. ск-ти возр.

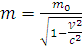, где – релят. масса, – масса покоя тела

Основное ур-е релят. динамики матер.точки должно быть инвариантно относительно преобразований Лоренца:

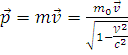
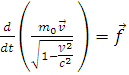- сила Минковского

Найдём выражение для релятив.кинет.эн-гии тела: пусть на тело массой действ. и тело изменяет свою ск-ть, тогда работа такой силы: . Эта работа приводит к измен. :

(*)

,

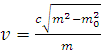→ в (*) →

Пусть ск-ть ч-цы мен-ся от 0 до , тогда .

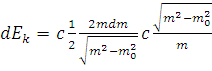
Интегрируем посл.выраж-е

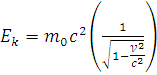
Рассмотрим предельный случай, когда

,

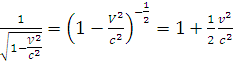
под массой понимают массу покоя .