25. Элементы акустики.

Акуст. кол-я (звук) – это кол-я, распростр. в упругой среде с частотой 16Гц≤U≤20кГц

1Гц – 1-о колебание за 1с; 16Гц ≥- инфразвук

20кГц≤ - ультразвук

Звуковая волна в газах и жидкостях может быть только продольной, а в тв. телах – и продольной и поперечной. Рассм-м х-ки звука:

Объективные физические	Субъективные психофизические
Частота	Высота тона
Интенсивность	Громкость
Спектр (состав)	Тембр (окраска)

Высота тона опр-ся частотой: чем больше частота, тем больше тон. сила звука – или громкость – это энергия, переносимая звуковой волной в 1-цу времени через единичную площадку, располож. перпенд. к источнику распространения звука. Субъект. громкость отличается от объективной, т.к. ухо человека наиболее чувствительно звуком с частотой 3-4кГц. Интенсивность I зв. волны – это среднее за период значение плотности потока Е, переносимое зв. волной. Порог слышимости – min I, когда еще испытывается звуковое ощущение. Для частот 1-4кГц порог слышимости I₀=10^-12Вт/м². Порог болевого ощущения – это I, когда звук вызывает ощущение боли ≈10Вт/м². В качестве интенсивности х-ки звука выбирают не силу звука I, а уровень силы звука (громкости), опред. соотношением

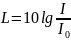
Уровень силы звука измеряется в децибелах, поэтому 0≤L≤130дБ. Логарифм. форма для L выбрана потому, что справедлив для челов. ощущений психофизиол. закон Вебер-Фехнера:

«Интенсивность ощущения пропорциональна логарифму степени раздражения, или интенсивность возрастает в геом. прогрессии, а громкость – в арифм. прогрессии».

Всякий реальный звук - это наложение целого ряда гармон. кол-ий с разл. частотами. Набор частот кол-ий, присутствующих в данном кол-и наз-ся акустическим спектром. Спектр – зависимость интенсивности от частоты. Различают сплошной и линейчатый спектры.

Сплошной спектр – шумы

Линейчатый спектр

Основной тон х-ся min частотой, а относит. интенсивность более высоких тонов (обертонов) определяет окраску (тембр) звука.

26.Модуль Юнга. Скорость звука.

Скорость звука.

Рассм. стержень длиной и площадью поперечного сечения S.

Δl =l- – абсол. Деформация ε= -относит-ая деформ-ия.

σ = 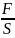- напрняжение

З-н Гука: Напряжение, прилож-ое к стрежню пропорционально относительному удлинению

σ = Eε – з-н Гука

Е – коэфф-т пропорциональности - модуль Юнга. – численно равен напряжению при относительной деыы-ции = 1: Е = σ/ε = 1

[E]= Па=

Для твёрдых кристалл-их тел з-н Гука запис-тся с учётом того,что напряжение и отн-ая деформ-ция представляет собой тензоры

= │ │

= │ │

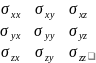З-н Гука тогда приобретает вид: i. j. k. l = 1,2,3

=

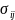Н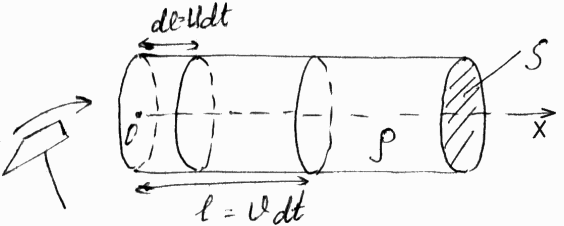 айдём скорость распространения звука в среде. Пусть вдоль однородного изотропного стержня вдоль оси x распростр-ся плоская одномерная продольная волна из-за деформации сжатия (растяж.)

Пусть вначале стержня часть среды смещается на величину dl за время dt, тогда dl = Udt (1)

За время dt возмущение распространяется со скоростью dv: l = vdt (2)

Т.к. волново дижение захватит расстояние l , то относительная деформация стержня:

По з-ну Гука:σ=Eε (4)

σ= Из (4) с учётом (5) и (3) имеем: F=SE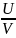 (6)

По 2 з. Ньютона : (7)

Масса в-ва, вовлечённое в волновое движение: m = ρSl = ρSdt (8)

Т.к скорость колеблющихся частиц = U, то изменение импульса участка l:

dp = mU = ρSVdtU F= = =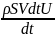ρSVU (10).

(6)=(10): ρSVU=SE ; ρV=

= ; = =

= ; =

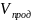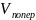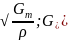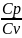
. Механический принцип относительности, преобразования Галилео.

Инерциальными наз. сис-мы отсчёта, в кот-ых свободные тела движутся прямолинейно, равномерно или покоятся.

Мех-ий принцип отностительности был установлен Галилеем в 1630.

1. Формулировка: Все мех-ие явления во всех инерциальных системах отсчёта происходят совершенно одинаково.

2. Никакими мх-ими опытами, проведёнными внутри системы нельзя установить: находятся ли инерциальные сис-мы отсчёта в состоянии покоя или равномерно движения: Е = m*c².

3. Современная форм-ка. Рассмотрим 2-е инерциальные системы S и S’ и пусть штрихован-ная система S’ движет-ся относительно не штрихованной S с постоянной V = const.

Пусть координаты т.М будет равны в S: x, y, z, t; S’ : x’, y’, z’, t’.

Ф-лы преобразования координат при переходе от одной системы к другой, очевидно, имеет вид:

(1)

Время t’=t течёт во все классической механике одинаково. Продифференцируем по времени с учётом dt=dt’

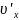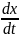= = – V= - V

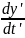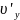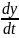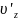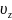= = – V= (2) = = – V= - V

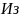ф-лы (2) вытекает:

(3)

Из ф-лы (3) вытекает теория о сложении скоростей в классич. Механике:

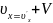
Продифференцируем соотношение (2) ещё раз по времени. (4)

(5)

=

Т. Е. скорости в инерциальной системе отсчёта относительны, а ускорения-абсолютны.

Рассмотрим 2-ой з-н 1Ньютона в S и S’, то:

m ’= ’ m =

Массы в классической механике не меняются.

Силы и определяются только взаимным расположением тел с их скоростями , поэтому не зависят от выбора инерциальной системы отсчёта: =

Основное уравнение динамики m = одинаково (неизменно) по форме при переходе от одной инерциальной системы отсчёта к другой. Тогда движение тела протекает одинаково во всех инерциальных системах отсчёта.

Формулировка: основное уравнение механики Ньютона инвариантно( неизменно) по форме относительно преобразований Галилея.