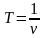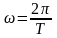- •1О. Кинематика поступательного движения.
- •2О. Кинематика вращательного движения.
- •3О. Динамика частиц. Закон ньютона.
- •4О. Неинерциальные системы отсчета (нсо). Силы инерции.
- •5О. Основное ур-ние динамики вращательного движения тв. Тела.
- •7О. Закон сохранения импульса.
- •8О. Работа.Мощность.Кинетическая энергия системы.
- •9О. Потенциальная энергия системы.
- •10. Закон сохранения энергии в механике
- •11О. Закон сохранения момента импульса.
- •12О. Движение тела переменной массы.
- •13О. Кинематика гарманических колебаний
- •14О. Гармонический осциллятор.
- •15О. Примеры гармонических осцилляторов.
- •16. Сложение гармонических колебаний одного направления и частоты.
- •17. Сложение взаимно перпендикулярных гармонических колебаний.
- •18. Затухающие колебания.
- •19.Вынужденные колебания. Резонанс.
- •20.Упругие волны в средах.
- •21О.Бегущие волны. Фазовая скорость. Длина волны. Волновое число.
- •22. Одномерное волновое ур-е. Энергия волны.
- •23. Распространение волн в средах с дисперсией. Групповая скорость, ее связь с фазовой скоростью.
- •24. Стоячие волны
- •25. Элементы акустики.
- •26.Модуль Юнга. Скорость звука.
- •28. Постулаты сто. Преобразование
- •29. Средства преобразования Лоренца.
- •30. Релятивистский закон сложения скоростей.
- •31. Интервал между событиями и его инвариантность в преобразовании Лоренца
- •32. Релятивистская динамика, кинетическая энергия сто.
- •33. Связь массы, энергии, импульса в сто
- •34О. Эффект Доплера
- •35О. Принцип эквиваленности.Понятие о ото
- •36О. Равновесие и течение жидкости и газа
- •37О. Уравнение неразрывности струи. Уравнение Бернулли
- •38. Уравнение Эйлера. Движение идеальной жидкости.
- •39. Течение вязкой жидкости. Формула Стокса.
- •40. Течение вязкой жидкости в трубах. Формула Пуазейля.
- •41. Динамический и статистический закономерности в физике.
- •42. Уравнение состояния идеального газа.
- •43. Основное уравнение молекулярно-кинетической теории газов (мкт).
- •44. Молекулярно-кинетический смысл абсолютной температуры.
- •45. Распределение Максвелла.
- •46. Параметрическая формула распределения Больцмана.
- •47. Распределение Гиббса.
- •48. Первое начало термодинамики.
- •49. Теплоемкость многоатомных газов.
- •50. Применение I начала термодинамики к изопроцессам(термодинамическим процессам).
- •51. Адиабатический процесс.
- •52. Политропный процесс
- •53. Теплоемкость и работа газа в политропном процессе
- •54. Обратимые и необратимые процессы, круговой процесс, тепловые двигатели, холодильные машины.
- •55. Цикл Карно. Максимальный кпд тепловой машины.
- •56. Технические циклы.
- •57. Второе начало термодинамики (6 формулировок).
- •58. Энтропия
- •59.Принцип возрастания энтропии
- •60. Определение энтропии неравновесной системы через статистический вес состояния. III начало термодинамики.
- •61. Метод термодинамических потенциалов (характеристических функций).
- •62. Явления переноса. Средняя длина свободного пробега молекул.
- •63. Коэффициент диффузии.
- •64. Теплопроводность. Коэффициент теплопроводности.
- •65. Уравнение теплопроводности.
- •66. Вязкость. Коэффициент вязкости.
- •67. Фазовые равновесия и превращения. Фазы и фазовые превращения.
- •68. Уравнение Клайперона - Клаузиса.
- •69. Реальные газы. Уравнение Ван – дер - Вальса .
- •70. Изотермы Ван-дер-Ваальса. Критич. Состояние. Внутр. Энергия реального газа.
- •71. Твёрдые тела.Теплоёмкость кристалла
- •72. Жидкости.Поверхн. Натяж. Жидк.
- •73. Смачивание и капиллярные явления
- •74. Принцип динамич. Отопления
- •75. Элементы физики полимеров
- •1О. Кинематика поступательного движения.
1О. Кинематика поступательного движения.
Д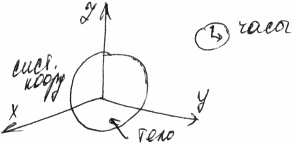 ля
описания движения тел.точек вводится
система отсчета. Система отсчета: тело
отсчета, система координат, часы. Движение
тела поступательно если любая прямая,
проведенная в теле и неизменно с ним
связанная перемещается оставаясь
параллельна самой себе.
ля
описания движения тел.точек вводится
система отсчета. Система отсчета: тело
отсчета, система координат, часы. Движение
тела поступательно если любая прямая,
проведенная в теле и неизменно с ним
связанная перемещается оставаясь
параллельна самой себе.
Материальной точкой называется тело, размерами которого можно пренебречь в данных условиях. Положение мат. точки задается радиус-вектором r ,проведенным из начала координат в искомую точку. Положение точки задается:

1) r = r(t)
2) x = x (t)
y = y (t)
z = z (t)
Положение точки можно также задавать пройденным путем вдоль траектории.
3) S = S(t)
В кинематике изучается движение тел, точек без учета причин вызывающих это движение.
Средняя скорость движения есть величина :
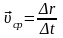
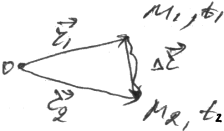
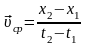
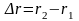
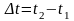
Скорость материальной точки есть производная от радиуса-вектора r по времени t. Скорость V направлена по касательной к траектории в сторону движения точки.
Vср
направлена по вектору перемещения .
.
Ед.измерения
физическая величина, обозначается [
] .
 = s
/ t
[
]= м/с
= s
/ t
[
]= м/с
В декартовой: x= dx/dt=x` ; y= dy/dt=y` z= dz/dt=z`
Ускорение. Среднее ускорение.
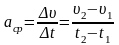
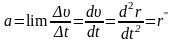
Ускорение точки есть производная от скорости по времени. а = d /dt
В декартовой: ax= d x/dt ay= d y/dt az= d z/dt
Простейший: a= /t [a]=м/с2
При
криволинейном движении точки ускорение
складывается из нормального
(центростремительного) и касательного
(тангенсального).
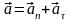
Нормальное ускорение направлено по нормали к траектории, к центру кривизны траектории, характеризует изменение скорости по направлению и равно:
 ; R-радиус
кривизны(окружности)
; R-радиус
кривизны(окружности)
Тангенсальное
ускорение направлено по касательной к траектории.
Характеризует изменение модуля скорости
со временем и равно:
направлено по касательной к траектории.
Характеризует изменение модуля скорости
со временем и равно:

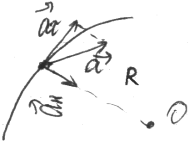
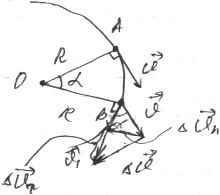 Пусть
точка движется по кривой , в частности
по окружности с переменной скоростью(меняя
модуль и направление скорости).
Пусть
точка движется по кривой , в частности
по окружности с переменной скоростью(меняя
модуль и направление скорости).
Перенесем скорость из точки А в т.В параллельно самой себе:
 ;
;

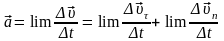


Из треугольника скоростей имеем
 ;
;
 (
( в радианах)
в радианах)
 ;
;

2О. Кинематика вращательного движения.
Движение тела называется вращательным, если все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Пусть точка вращается по окружности радиуса R.
Положение точки на окружности характеризуется углом поворота φ (угловым перемещением), который отсчитывается от некоторого направления ОХ.
У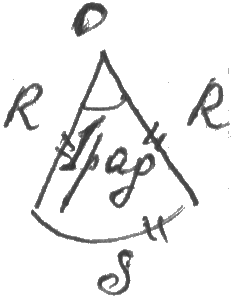 гол
φ измеряется в радианах [φ] = рад; 360° =
2π R/R ≈6,28
рад; 1 рад ≈ 57,3°
гол
φ измеряется в радианах [φ] = рад; 360° =
2π R/R ≈6,28
рад; 1 рад ≈ 57,3°
Угловая скорость есть производная от угла и поворота по времени t.
 [ω]= рад/с= 1/с
[ω]= рад/с= 1/с
ω- есть вектор, направленный вдоль оси вращения. Направление ω характеризуется правилом правого винта: если рукоятки винта вращаются по направлению движения точки, то поступательное движение винта указывает направление вектора ω . Степень неравномерности вращения характеризуется угловым ускорением. Угловое ускорение есть производная от угловой скорости по времени, или вторая производная от углового перемещения по времени.
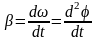

Вектор ускорения β направлен вдоль оси вращения в ту же сторону, что и ω при ускоренном вращении : [β]= рад/с2 или 1/с2.
Найдем связь линейных и угловых скоростей ускорения:
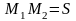 ;
;
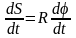 ;
;
 R=const ; υ
=ωR
R=const ; υ
=ωR
Касательная
ускорения
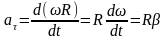
Нормальное ускорение
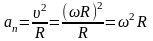
Частный случай : ω=const (равномерное), тогда ω=2πν
Период обращения Т – время за которое совершается полный оборот.;