9. Наибольшее и наименьшее значение функций в замкнутой ограниченной области.

Пусть функция   непрерывна в замкнутой ограниченной области G, дифференцируема внутри этой области. Чтобы найти наибольшее и наименьшее значения функции в этой области, нужно:

1)найти критические точки, принадлежащие этой области, и вычислить в них значения функции;

2)найти наибольшее и наименьшее значения функции на границе области;

3)из всех найденных значений выбрать наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значения функции   в треугольнике, ограниченном прямыми  ,  ,  .

Решение. 1)найдем критические точки функции.    ;    .

Н айденная критическая точка   не принадлежит области.

2)Исследуем границу области. На участке AB: y=1,  . Функция имеет вид  то есть  ;   при всех  функция монотонно возрастает на этом участке, поэтому  ,  .

На участке BC:  ,   Функция имеет вид  , то есть  ,   при  –критическая точка на участке BC.  ;  .

На участке AC: x+y=1, или    . Функция имеет вид  , то есть  ;  ;   при  –критическая точка на участке AC.  .

3)Выберем наибольшее и наименьшее из найденных значений:           Получим     где  ,  .

10. Условный экстремум функции двух переменных. Экономический смысл множителей Лангранжа.

Условный экстремум. Метод Лагранжа.

       Условным экстремумом функции   в точке   называется экстремум этой функции, достигнутый при условии, что переменные x и у в окрестности данной точки удовлетворяют уравнению связи  .

       Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие  . Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует  , то, подставив в  , получим функцию одной переменной . В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа

       Для отыскания условного экстремума составляют функцию Лагранжа: . Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

       Достаточным условием, из которого можно выяснить характер экстремума, служит знак  . Если в стационарной точке  , то функция   имеет в данной точке условный минимум, если же  , то условный максимум.

Примечание (желательное для более полного понимания текста): показать\скрыть

       Есть и другой способ для определения характера экстремума. Из уравнения связи получаем:  ,  , поэтому в любой стационарной точке имеем:

       Второй сомножитель (расположенный в скобке) можно представить в форме  . Определитель H называется гессианом функции Лагранжа. Если  , то , что указывает на условный максимум. Аналогично, при   имеем  , т.е. имеем условный минимум функции  .

Алгоритм исследования функции двух переменных на условный экстремум

1. Составить функцию Лагранжа  2. Решить систему

3. Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:

• Составить гессиан и определить его знак, • С учетом уравнения связи вычислить знак  .

Пример №1

Найти условный экстремум функции   при условии  .

Решение

       Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости   для точек ее пересечения с цилиндром  .

       Выразить одну переменную через другую из уравнения связи и подставить ее в функцию   несколько затруднительно, поэтому будем использовать метод Лагранжа.

Обозначив  , составим функцию Лагранжа:

. 

Запишем систему уравнений для определения стационарных точек функции Лагранжа:

       Если предположить  , то первое уравнение станет таким:  . Полученное противоречие говорит о том, что  . При условии   из первого и второго уравнений имеем:  . Подставляя полученные значения в третье уравнение, получим:

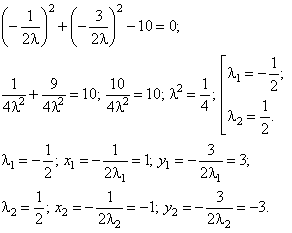
      Итак, система имеет два решения:  ,  ,   и  ,  ,  . Выясним характер экстремума в каждой стационарной точке:   и  .  Для этого вычислим гессиан в каждой из точек.

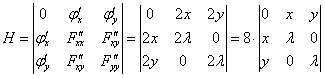
В точке   получим: 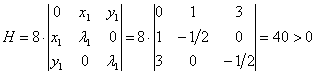, поэтому в точке   функция имеет условный максимум,  .

Аналогично, в точке   найдем:  . Так как , то в точке   имеем условный минимум функции  , .

       Вопрос о характере экстремума в стационарных точках и можно решить и без использования гессиана. Определим знак   в каждой стационарной точке:

       При    , поэтому функция имеет в точке   условный максимум. Аналогично, в точке   получим условный минимум функции  . Отметим, что для определения знака   не пришлось учитывать связь между dx и dy, ибо знак   очевиден без дополнительных преобразований. В следующем примере для определения знака   уже будет необходимо учесть связь между dх и dу.

Пример №2

Найти условный экстремум функции   при условии  .

Решение

Первый способ (метод Лагранжа)

. Функция Лагранжа:  .

       Решив систему, получим:   и  . Имеем две стационарные точки:   и  . Выясним характер экстремума в каждой стационарной точке с использованием гессиана.

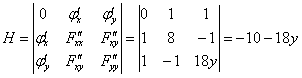
       В точке    , поэтому   есть точка условного минимума функции  ,  . В точке    , посему в данной точке функция имеет условный максимум,  .

       Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке  :

Из уравнения связи   имеем:  .

       Так как  , то   является точкой условного минимума функции . Аналогично,  , т.е.   - точка условного максимума.

 

Второй способ

       Из уравнения связи   получим:  . Подставив   в функцию  , имеем:

        Таким образом, задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.

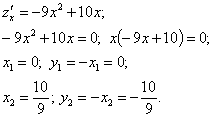        Получили точки   и   . Дальнейшее исследование известно из курса дифференциального исчисления функции одной переменой. Исследуя знак   в каждой стационарной точке или проверяя смену знака   в найденных точках, получим те же выводы, что и при решении первым способом.

        Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака  .

Пример №3

        Найти наибольшее и наименьшее значения функции  , если переменные x и yположительны и удовлетворяют уравнению связи  .

Решение

Составим функцию Лагранжа:

Найдем стационарные точки функции Лагранжа:

        Все дальнейшие преобразования осуществляются с учетом  . Из второго уравнения выразим   и подставим найденное значение в первое уравнение: Подставляя   в третье уравнение, получим: .

        Так как  , то  . Характер экстремума в точке   определим, исходя из знака  .

Так как  , то: 

        В принципе, здесь можно сразу подставить координаты стационарной точки  и параметра  , получив при этом:

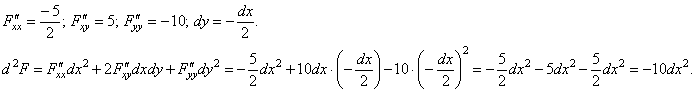
        Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше   представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

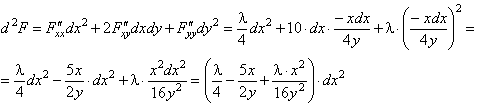Подставляя  , получим:

.

        Так как  , то точка   есть точкой условного максимума функции , причём  .