6. Частные производные высших порядков.

Рассмотрим функцию двух переменных n=2,  . Предположим, что функция имеет частные производные

,                        ,

которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы.

Определение 1. Частные производные от частных производных первого порядка называются частными производными второго порядка.

 =  ,                         =  .

 =  ,                        =  .

 

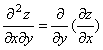Две последние называют смешанными производными.

Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:

.

 

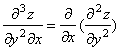Определение 2. Частной производной n-го порядка называется частная производная от частной производной (n-1)-го порядка. Частных производных n-го порядка от функции двух переменных 2ⁿ штук.

Частная производная порядка р функции   имеет вид

, где  .

Теорема. Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.

.

Пример.  .

,                 ,

,  ,     ,  ,

.

7. Экстремум функции двух переменных. Необходимые условия экстремума.

8. Достаточные условия экстремума функции двух переменных.

Говорят, что функция   имеет максимум в точке  , т.е. при   , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Говорят, что функция   имеет минимум в точке  , т.е. при  , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция   достигает экстремума при  , то каждая частная производная первого порядка от   или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку   функция   имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка   является критической точкой функции  , т.е. , тогда при  : 1)   имеет максимум, если дискриминант   и  , где 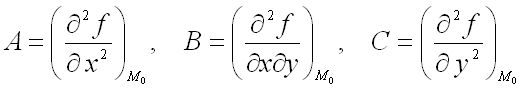 ; 2)   имеет минимум, если дискриминант   и  ; 3)   не имеет ни минимума, ни максимума, если дискриминант  ; 4) если   , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

 

 

 

Примеры решения задач

Пример 1. Исследовать на экстремум функцию  .

Решение.

На первом шаге, в соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

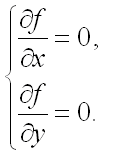
Частные производные первого порядка от функции   равны:

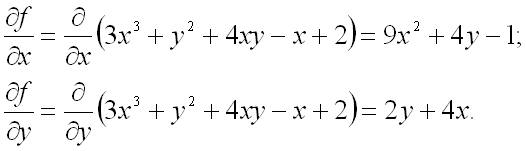
Приравняем их к нулю и решим систему уравнений:

Выпишем отдельно первое уравнение системы и найдем его корни:

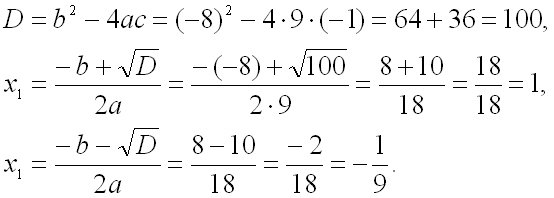
Подставим найденные значения переменной   во второе уравнение системы:

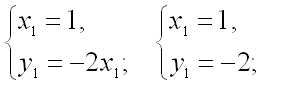 и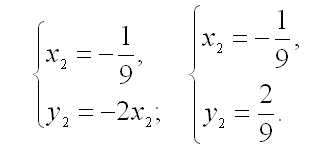 

Таким образом, получили две точки   и 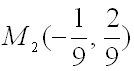 , в которых будет продолжено исследование функции   на экстремум.

На втором шаге найдем все вторые частные производные от функции  :

 

  На третьем шаге для каждой из точек   и   установим наличие экстремума функции   (для этого вычислим значения вторых производных и найдем знак дискриминанта   в указанных точках).

1) Для точки  :

Так как дискриминант больше нуля и  , то функция   имеет минимум в точке  : .

2) Для точки  :

Так как дискриминант меньше нуля, то функция   не имеет в точке  ни минимума, ни максимума.

Ответ: в точке   функция   имеет минимум .