44. Теорема о структуре общего решения линейного однородного дифференциального уравнения.

Теорема 4. Если   - линейно независимые на   решения линейного однородного дифференциального уравнения  -го порядка   с непрерывными коэффициентами  , то функция

,                                                   (9)

где   - произвольные постоянные, является общим решением уравнения  , т. е. сумма (9) при любых  , есть решение этого уравнения и, обратно, всякое решение этого уравнения представимо в виде суммы (9) при соответствующих значениях  .

Доказательство. Мы уже знаем, что сумма (9) при любых   есть решение уравнения  . Пусть, обратно,   есть произвольное решение этого уравнения. Положим

.                   (10)

Для полученных чисел   составим линейную систему уравнений относительно неизвестных чисел  :

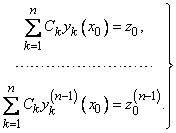                                                             (11)

Определитель системы (11)   не равен нулю, так как функции   — линейно независимые на   решения уравнения  . Поэтому существует единственная система чисел  , удовлетворяющих уравнениям (11). Подставляя их в (9), получим решение нашего уравнения в виде

,

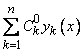удовлетворяющее тем же начальным условиям (10), которым удовлетворяет  . Но тогда на основании теоремы существования и единственности имеет место равенство  . Теорема доказана.

Таким образом, чтобы найти общее решение однородного уравнения  , достаточно найти какие-нибудь   линейно независимых решений этого уравнения, и тогда общее решение будет их линейной комбинацией (9). Напомним, что любую совокупность из   линейно независимых частных решений уравнения   мы условились называть фундаментальной системой решений этого уравнения.

Возникает вопрос, всегда ли существует фундаментальная система (3) с непрерывными коэффициентами? Покажем, что существует.

Зададим   векторов

Каждому из этих векторов приведем в соответствие решение   уравнения (3). Именно, пусть   есть решение, удовлетворяющее следующим начальным условиям:

Определитель Вронского   для этой системы решений при  , очевидно, есть определитель матрицы, составленной из векторов  . Он равен 1:

.

Но тогда система решений   линейно независима, потому что для зависимой системы определитель Вронского был бы тождественно равен нулю.

45. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянных C₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x, C₁₀ , ..., C_n0)удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

Справедливо следующее утверждение ( теорема о структуре общего решения линейного неоднородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x), y₂(x),..., y_n(x)образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x) + y*(x),

где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение с непрерывными на (e, ∞) коэффициентами и непрерывной правой частью

частным решением которого является функция

Фундаментальную систему решений соответствующего однородного уравнения образуют функции y₁(x) = ln x , y₂(x) = x.

Общее решение неоднородного уравнения имеет вид