31. Вычисление объема тела по площадям параллельных сечений.

Рассмотрим тело D, ограниченное плоскостями х = а  и  х = b (рис. 247).

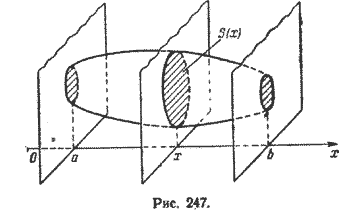
Через S(x) обозначим площадь сечения тела D плоскостью, проходящей через точку с абсциссой х   [а; b] и перпендикулярной оси Ох. Будем предполагать, что

1) функция S(x) непрерывна на [а; b];

2) для любых x₁ и x₂ из [а; b] сечения тела D плоскостями х =  x₁ и х =  x₁ таковы, что одно из них проектируется в другое.

Тело D, обладающее этими свойствами, будем называть телом с допустимыми параллельными сечениями.

Теорема. Объем тела с допустимыми параллельными сечениями вычисляется по формуле

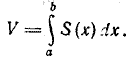       (1)

Отрезок  [а; b] точками

разобьем на п отрезков [х_i—1 ; х_i] длины

Пусть т_i  и M_i — наименьшее и наибольшее значения функции S(x) на отрезке   [х_i—1 ; х_i] .

Плоскостями х = х_i,  где i = 1, 2, ..., п — 1, тело D разобьем на n слоев. Выделим i-й слой, соответствующий отрезку [х_i—1 ; х_i], и построим два цилиндра высрты Δ х_i :  один с основанием площади M_i  , содержащий i-й слой, а другой с основанием площадит_i  ,  содержащийся в i-м слое (рис. 248).

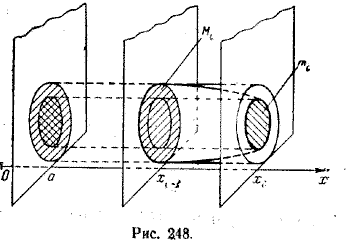
Объемы этих цилиндров равны M_i Δ х_i  и т_i Δ х_i.

Произведя указанные построения для каждого слоя, получим два ступенчатых тела D'_n и D"_n таких, что D'_n < D < D''_n.

Их объемы равны

Так как функция S(x) непрерывна, то V'_n и V"_n  при  п —>  ∞ имеют один и тот же предел, равный   .

Следовательно, объем тела D вычисляется по формуле (1).

Замечание. Можно доказать, что формула (1) остается справедливой и в том случае, когда условие 2) для тела D не выполняется.

Задача. Определить объем тела, отсекаемого от прямого кругового цилиндра плоскостью, проходящей через диаметр основания и составляющей с плоскостью основания угол α (α < 90°). Радиус основания цилиндра равен R.

Введем систему координат так, как показано на рис. 249, и рассмотрим сечения данного тела плоскостями, перпендикулярными оси Оx.

Вычислим площадь сечения плоскостью, проходящей через точку А с абсциссой х, |х| < R. Это сечение представляет собой прямоугольный треугольник ABC, и поэтому

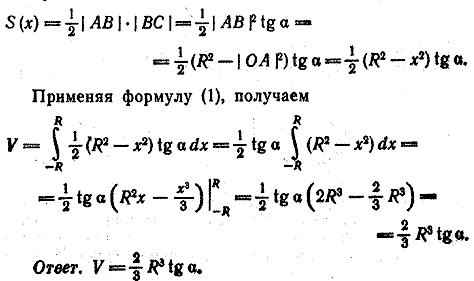
32. Объем тела вращения. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси

Пример 1

Вычислить объем тела, полученного вращением фигуры, ограниченной линиями  ,   вокруг оси   .

Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости   необходимо построить фигуру, ограниченную линиями  ,  , при этом не забываем, что уравнение   задаёт ось  . Как рациональнее и быстрее выполнить чертёж, можно узнать на страницах Графики и свойства Элементарных функций и Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.

Чертёж здесь довольно прост:

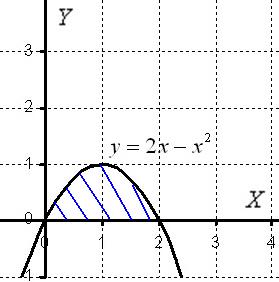
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси  . В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси  . На самом деле у тела есть математическое название, но в справочнике что-то лень смотреть, поэтому едем дальше.