28. Вычисление площадей плоских фигур в прямоугольных координатах.

а) Допустим, что фигура предполагает наличие границы

является криволинейной трапецией и , при условии, что на

Если находится ниже оси (рис. 18.1), то

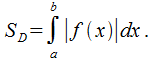
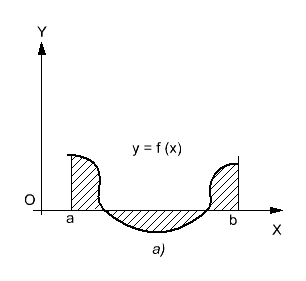
Рис. 18.1

Пример:

 

 

(рис. 18.1, б).

 

 

б) Предположим, что для фигуры харакерно наличие границы Площадь (рис. 18.2, а),

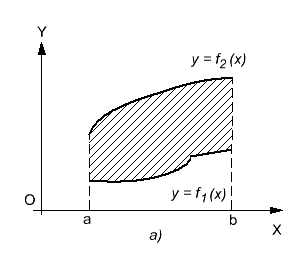
Рис. 18.2

 соответственно получаем формулу

В общем случае площадь находится с помощью формулы

 

Пример:

(рис. 18.2, б).

 

 

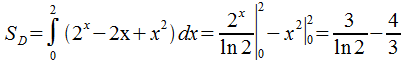
29. Вычисление площади плоских фигур в полярных координатах.

Любая точка в полярной системе координат задается полярным углом   и соответствующим полярным радиусом  .   - это угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки), а   - это расстояние от заданной точки до начала координат (полюса).

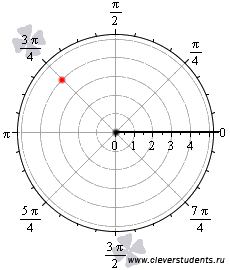
На рисунке полюс изображен черной точкой, полярная ось – черным жирным лучом, а красная точка определяется углом   и расстоянием до полюса  .

На практике очень часто полярную систему координат рассматривают вместе с прямоугольной декартовой, совмещая начала координат и полярную ось с осью абсцисс.

Связь декартовых и полярных координат задается соотношениями   и обратно  .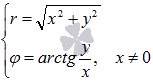

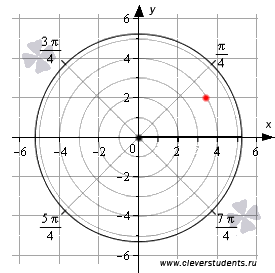
На чертеже красная точка имеет координаты  , а в полярной системе координат определяется углом   и расстоянием до полюса  .

В полярной системе координат равенство   задает луч, выходящий из полюса и составляющий угол   с полярной осью (  задается в радианах или градусах). Полярная ось задается уравнением  . Равенство   задает окружность с центром в начале координат радиуса C. В свою очередь функция   определяет некоторую линию в полярных координатах.

Обратите внимание, что мы будем считать функцию   всегда НЕОТРИЦАТЕЛЬНОЙ, так как с геометрической позиции она задает расстояние от полюса до точки для данного значения угла  . Однако, иногда рассматривают и отрицательные значения функции  , так что желательно уточнить у преподавателя его отношение к этому вопросу.

Ниже на рисунке приведены несколько примеров линий в полярной системе координат.

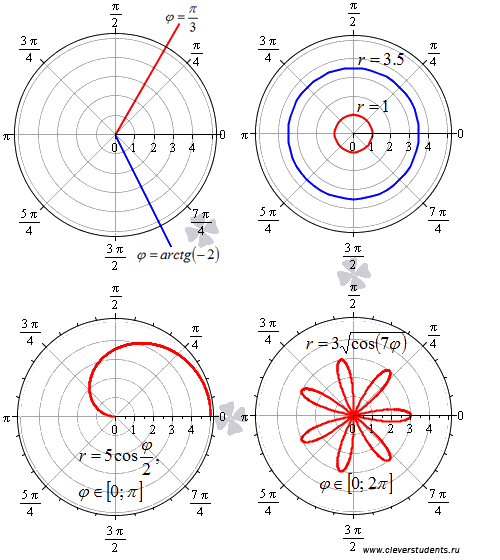
Теперь можно дать определение криволинейного сектора.

Определение.

Криволинейный сектор – это фигура, ограниченная лучами   и некоторой линией  , которая непрерывна на отрезке  .

На чертеже приведены несколько примеров криволинейных секторов.

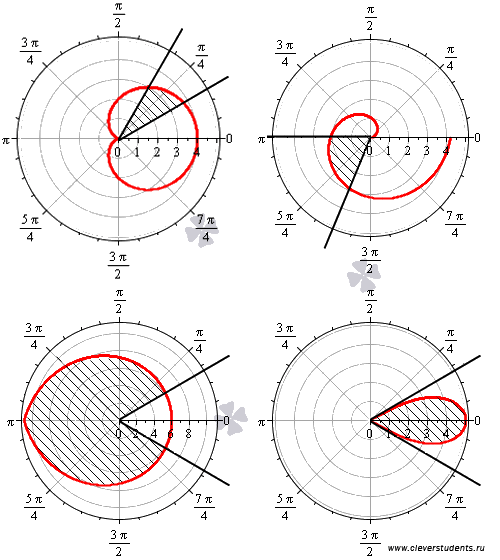
На последнем рисунке фигура заключена между лучами  , но они не являются ее границами.

Площадь криволинейного сектора - вывод формулы.

Выведем формулу для вычисления площади криволинейного сектора.

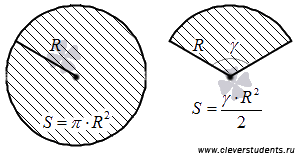
Для этого нам понадобится известная из школьного курса геометрии формула площади кругового сектора радиуса R с внутренним углом  :   (  задается в радианах).

Разобьем криволинейный сектор на n частей такими лучами  , что   и   при  .

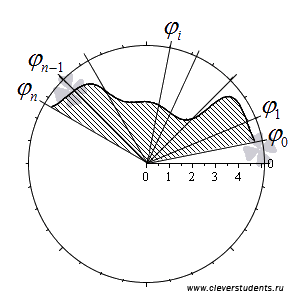
В силу свойств площади фигуры, площадь исходного криволинейного сектора  представится суммой площадей криволинейных секторов   на каждом участке разбиения  .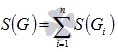

Пусть   и   - наименьшее и наибольшее значение функции   на i-ом отрезке  . На каждом таком отрезке построим по два круговых сектора   и   с радиусами   и   соответственно.

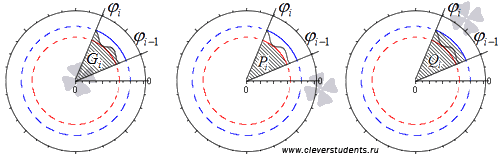
Обозначим P и Q фигуры, являющиеся объединением круговых секторов   и   соответственно.

Их площади будут равны   и  , причем  .

Так как функция   непрерывна на отрезке  , то на этом отрезке будет также непрерывна функция  . Для этой функции S(P) и S(Q) можно рассматривать аналогично нижней и верхней суммам Дарбу, что приводит нас к равенству

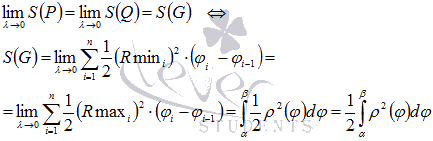
Таким образом, площадь криволинейного сектора находится по формуле 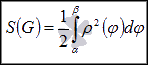 .