
- •Функции двух и трех переменных как функции точки
- •Геометрическое изображение функции двух переменных с помощью поверхностей и линий уровня.
- •Предел функции. Непрерывность в точке и в области.
- •Частные производные функции нескольких переменных, геометрический смысл частных производных функции двух переменных.
- •Полный дифференциал функции нескольких переменных.
- •3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( , либо какой-нибудь другой), по которой ведется дифференцирование.
- •3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( , либо какой-нибудь другой), по которой ведется дифференцирование.
- •Частные производные высших порядков.
- •Экстремум функции двух переменных. Необходимые условия экстремума.
- •Достаточные условия экстремума функции двух переменных.
- •Наибольшее и наименьшее значение функций в замкнутой ограниченной области.
- •Условный экстремум функции двух переменных. Экономический смысл множителей Лангранжа.
- •Первообразная. Неопределенный интеграл.
- •Некоторые дополнительные интегралы
- •Основные свойства неопределенного интеграла.
- •Метод замены переменной в неопределенном интеграле.
- •Метод интегрирования по частям.
- •Интегралы от логарифмов
- •Интегралы от экспоненты, умноженной на многочлен
- •Интегралы от тригонометрических функций, умноженных на многочлен
- •Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен
- •Интегралы от некоторых функций, содержащих трехчлен.
- •Интегрирование рациональных дробей.
- •Интегрирование иррациональных функций.
- •Интегралы от корней. Типовые методы и приемы решения
- •Интегрирование биномиальных интегралов
- •2) Случай второй
- •Интегрирование тригонометрических функций.
- •Использование тригонометрических формул
- •Понижение степени подынтегральной функции
- •Метод замены переменной
- •Универсальная тригонометрическая подстановка
- •См. Конспект
- •См. Конспект
- •Определение определенного интеграла. Основные свойства.
- •Определение
- •Обозначения
- •Свойства
- •Геометрический смысл
- •Теорема об интеграле с переменным верхним пределом.
- •Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла. Метод интегрирования по частям в определенном интеграле
- •Вычисление площадей плоских фигур в прямоугольных координатах.
- •Вычисление площади плоских фигур в полярных координатах.
- •Площадь криволинейного сектора - вывод формулы.
- •Примеры вычисления площади криволинейного сектора.
- •Вычисление длины дуги плоской кривой.
- •Вычисление объема тела по площадям параллельных сечений.
- •Объем тела вращения. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
- •Как вычислить объем тела вращения?
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
- •Интегралы с бесконечными пределами интегрирования.
- •Несобственный интеграл с бесконечным пределом (ами) интегрирования
- •Несобственные интегралы от неограниченных функций
- •Интегралы от неограниченных функций.
- •Признаки сходимости несобственных интегралов.
- •Обыкновенные дифференциальные уравнения (основные понятия).
- •Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши (формулировка).
- •Дифференциальные уравнения с разделяющимися переменными.
- •Дифференциальные уравнения с однородными функциями.
- •Как решить однородное дифференциальное уравнение?
- •Линейные дифференциальные уравнения первого порядка и уравнения Бернулли.
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •Метод повторного интегрирования правой части
- •В дифференциальном уравнении в явном виде отсутствует функция
- •В дифференциальном уравнении в явном виде отсутствует независимая переменная
- •Линейные однородные уравнения n-го порядка, свойства их решений.
- •Теорема о структуре общего решения линейного однородного дифференциального уравнения.
- •Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.
- •Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Характеристическое уравнение имеет два различных действительных корня
- •Характеристическое уравнение имеет два кратных действительных корня
- •Характеристическое уравнение имеет сопряженные комплексные корни
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида.
- •Общее решение неоднородного дифференциального уравнения:
См. Конспект
См. Конспект
См. КР
Определение определенного интеграла. Основные свойства.
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Определение
Пусть ![]() определена
на
определена
на ![]() .
Разобьём
на
части с несколькими произвольными
точками
.
Разобьём
на
части с несколькими произвольными
точками ![]() .
Тогда говорят, что произведено
разбиение
.
Тогда говорят, что произведено
разбиение ![]() отрезка
отрезка ![]() Далее
выберем произвольную точку
Далее
выберем произвольную точку ![]() ,
, ![]() ,
,
Определённым
интегралом от функции
на
отрезке
называется
предел интегральных сумм при стремлении
ранга разбиения к нулю ![]() ,
если он существует независимо от
разбиения
и
выбора точек
,
если он существует независимо от
разбиения
и
выбора точек ![]() ,
то есть
,
то есть
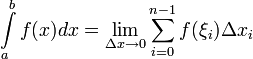
Если существует указанный предел, то функция называется интегрируемой на по Риману.
2)Определение(более легкое для запоминания):
Приращение F(b)-F(a)любой из первообразных F(x)+с называется определенным интегралом.
Обозначения
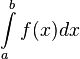
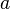 —
нижний
предел.
—
нижний
предел.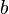 —
верхний
предел.
—
верхний
предел.— подынтегральная функция.
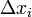 —
длина
частичного отрезка.
—
длина
частичного отрезка.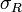 —
интегральная
сумма от функции
на
соответствующей
разбиению
.
—
интегральная
сумма от функции
на
соответствующей
разбиению
.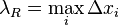 —
максимальная
длина част. отрезка.
—
максимальная
длина част. отрезка.
Свойства
Если функция интегрируема по Риману на , то она ограничена на нем.
Геометрический смысл
Определённый
интеграл 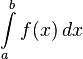 численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми
численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми ![]() и
и ![]() и
графиком функции
.
и
графиком функции
.
Теорема об интеграле с переменным верхним пределом.
Рассмотрим функцию y = f(x), интегрируемую на отрезке [а, b]. Если х на промежутке [a, b], то функция f(x) интегрируема также на любом отрезке [а, х]. Предположим, что х меняется на отрезке [а, b], тогда на этом отрезке определена функция
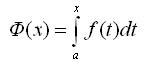
(Переменную интегрирования обозначили буквой t, переменный верхний предел - буквой х).
Теорема 1. Если функция у = f(x) интегрируема на отрезке [а, b], то функция Ф(х) непрерывна на этом отрезке.
Теорема 2. Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела. т.е.
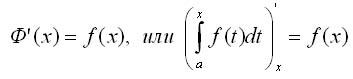
Следствие 1. Если функция f(x) непрерывна на отрезке [а, b], то при любом х
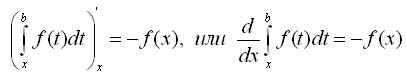
Следствие 2. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции.
Другими словами, для любой непрерывной функции существует первообразная.
Эти функции не являются элементарными; первообразные указанных подынтегральных функций не выражаются через элементарные функции.
Все приведенные функции хорошо изучены, для них составлены таблицы значений, эти функции находят широкое применение.
Связь между определенными и неопределенными интегралами выражает следующая теорема Ньютона - Лейбница, называемая основной теоремой интегрального исчисления.
Теорема 3. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной для верхнего и нижнего предела интегрирования:
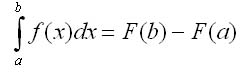
где F'(x)=f{x).
Эта формула называется формулой Ньютона - Лейбница; ее можно переписать в виде
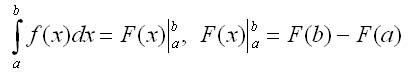
левая часть второй формулы читается так: «двойная подстановка от а до b для функции F(x).
Замечание. Интеграл с переменным верхним пределом интегрирования используется при определении многих функций. К таким функциям относятся, например:
Интегральный синус
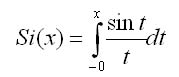
Интегральный косинус
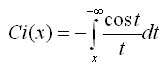
Интегральный логарифм
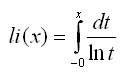
Интегральная показательная функция
Интеграл вероятностей
