9. Уравнение настройки и характеристика групповых передач.

Расширение диапазона регулирования привода достигается последовательным соединением групповых передач. При проектировании привода необходимо знать общие кинематические закономерности множительных групп, в частности, взаимосвязь передаточных отношений отдельных передач в группе.

(1)

Это выражение устанавливает относительную связь между передаточными отношениями передач данной группы и называется уравнением настройки групповых передач. Согласно уравнению настройки 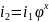; ;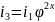 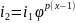т.е. передаточные отношения передач множительной группы образуют геометрический ряд со знаменателем 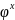. Из равенств 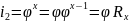следует, что знаменатель ряда передаточных отношений данной группы равен произведению знаменателя ряда частот вращения и диапазона регулирования, которые дают группы, предшествующие данной в порядке переключения, т.е.

(2)

Каждая группа передач является множительной для совокупности групп передач, кинематически ей предшествующей, поэтому уравнения (1) и (2) выражают основную общую закономерность построения групповых передач привода, обеспечивающего геометрический ряд частот вращения.

Показатель x при φ в уравнении настройки групповых передач называется характеристикой множительной группы передач. Из вывода уравнения настройки следует, что характеристика группы передач численно равна количеству ступеней скорости, которые дают группы, предшествующие в порядке переключения данной. Значение характеристики показывает также, на сколько ступеней изменяется скорость при переключении передач данной группы. Первая в порядке переключения группа (основная группа) является множительной только для одиночных передач, дающих постоянное значение скорости. Поэтому характеристика x₀ основной группы равна единице: x₀=1. Второй в порядке переключения группе (первой переборной) кинематически предшествует основная группа, которая обеспечивает число ступеней скорости, равное количеству ее передач p₀. Следовательно, характеристика x₁ первой переборной группы равна числу передач в основной группе: x₁=p₀.

Основная и первая переборные группы создают число ступеней ско-рости, равное произведению количества их передач, т.е. p₀p₁. Поэтому характеристика третьей в порядке переключения группы (второй переборной) x_ΙΙ=p₀p_Ι. Характеристика i-той группы передач в приводе x_i=p₀p_Ιp_ΙΙ…p_i-1.

10. Связь между передаточными отношениями и диапазонами регулирования группы и привода в целом. Проверка осуществимости варианта привода.

Запишем структурную формулу z = p₁(x₁) p₂(x₂)…p_m(x_m)

Передаточные отношения передач группы имеют предельные значения, поэтому ее параметры р и х не могут быть произвольными. В этой связи не все возможные варианты структуры привода осуществимы.

Проверка осуществимости варианта структуры привода является обязательным этапом его проектирования. Решение этой задачи связано с определением связи между передаточными отношениями и диапазоном регулирования групповой передачи.

Предельные значения передаточных отношений групповых передач установлены практикой станкостроения. Они зависят от назначения привода (главного движения или подачи) и конструкции зубчатых колес (прямозубые или косозубые).

Для привода главного движения с прямозубыми колесами 0,25 ≤ i ≤ 2, т.е. [i_max] = 2, [i_min] =0,25. Следовательно, допускаемый диапазон регулиро-вания группы [R_p] = [i_max]/[i_min]= 8.

Для передач с косозубыми колесами 0,25 ≤ i ≤ 2,5, тогда [i_max]= 2,5; [i_min] =0,25; [R_p] = 10.

В коробках подач обычно применяются только прямозубые колеса, для которых 0,2 ≤ i ≤ 2,8. Следовательно, [i_max] = 2,8; [i_min] =0,2; [R_ps] = 14.

Фактический диапазон регулирования групповой передачи должен быть меньше допустимого, поэтому вариант структуры привода осуществим, если выполняется условие

R_p = φ^(p-1)x≤ [R_p]. (1)

Проверка осуществимости варианта структуры привода проводится по условию (1) для последней в порядке переключения группы, так как ее характеристика имеет максимальное значение.