5. Определение предельных частот вращения и диапазона регулирования привода

При разработке приводов станков следует учитывать, что имеющиеся системы электро- и гидроприводов позволяют решить многие задачи, связанные с регулированием и изменением скорости и направления движения, которые раньше решали лишь с помощью механических устройств.

Важнейшими исходными данными для проектирования привода главного движения являются диапазон регулирования частоты вращения Rnи мощность N, передаваемая приводом. Эти технические характеристики зависят от служебного назначения станка, их определяют на основе анализа технологических процессов обработки множества деталей и соответствующей номенклатуры режущего инструмента, оговоренных техническим заданием на проектирование

При этом Rn=nmax/nmin

Для приводов с главным вращательным движением nmax и nmin – макисимальная и миним частоты вращения шпинделя, определяемые по предельным(максимальным и минимальным) для всех операций скоростям резания vmin и vmax и предельным для них же размерам обработки DmaxDmin;

nmax=1000vmax/ПDminnmin=1000/ ПDmax

предельные значения частот двойных ходов:

nmax=500vmax/П Lminдв х/мин nmin=500/ ПLmaxдв х/мин

При назначении диапазона регулирования и мощности привода необходимо учитывать, что увеличение их значений усложняет и удорожает привод, а занижение приводит к уменьшению производительности из-за невозможности применения экономически выгодных режимов обработки для всей требующей совокупности операций.

6. Ряды частот движения и подач (геометрический и арифметический ряды), стандартные значения знаменателя геометрического ряда и выбор его значения.

Создаваемый приводом ряд частот вращения характеризуется их предельными и промежуточными значениями. Расчетное значение частоты вращения шпинделя в каждом конкретном случае определяется исходя из допускаемой скорости резания v и диаметра обработки d. Учитывая множество возможный сочетаний значений v и d, обеспечение для всех случа­ев оптимального режима резания возможно при бесступенчатом регулировании скорости вращения шпинделя. Однако более распространено сту­пенчатое регулирование скорости исполнительных органов. В этой связи возникает задача определения промежуточных значений ряда частот вращения между n_min и n_max, обеспечивающих наилучшее приближение к оптимальным режимам резания и наименьшую потерю производительности обработки.

Пусть имеем ряд частот вращения с z ступенями скорости n₁, n₂, n₃,...n_i n_i+1,...n_z, где n₁ = n_min; n_z = n_max - его предельные значения. Для обработки со скоростью резания v (м/мин) поверхности диаметром d (мм) не­обходима частота вращения шпинделя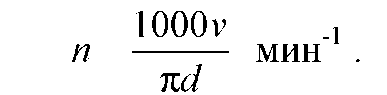

В общем случае расчетная частота n не совпадает ни с одним из зна­чений членов ряда, т.е. n_i < n <n_i+₁. Тогда v_i < v < v_i+1, где v_i и v_i+1 - значе­ния скорости резания, соответствующие для данного диаметра d частотам вращения n_i и n_i+1 .

Для обеспечения заданной стойкости режущего инструмента обра­ботка должна производиться со скоростью резания v_i меньшей или равной расчетному значению v. При v_i < v неизбежна потеря экономически выгод­ной скорости резания. Абсолютная потеря скорости Δν= ν – ν_i а относительная

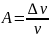
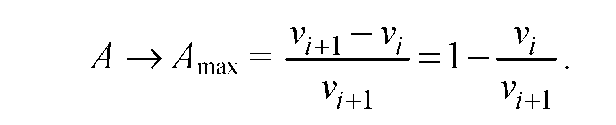
Поскольку скорость резания v пропорциональна частоте вращения n, то максимальная относительная потеря скорости составляет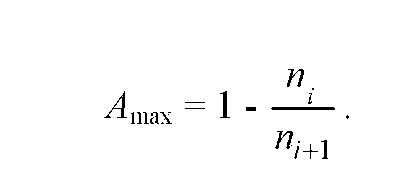

Станок будет работать в равноценных эксплуатационных условиях на всем диапазоне регулирования частоты вращения шпинделя, если макси­мальная относительная потеря скорости будет величиной постоянной, т.е.

A_max = const. Следовательно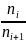 = const, что справедливо только для гео­метрического ряда, у которого гдеφ - знаменатель геометрической прогрессии. Таким образом, ряд частот вращения шпинделя должен быть гео­метрическим.При обработке резанием производительность формообразования, измеряемая площадью поверхности, обработанной в единицу времени, пропорциональна скорости резания v.Следовательно, при геометрическом ряде частоты вращения шпинделя максимальная относительная потеря производительности формообразования

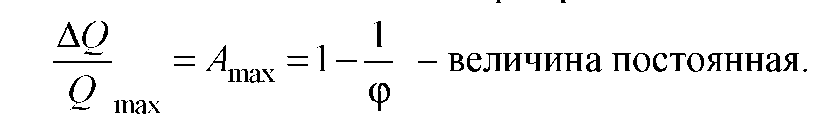
Любой член геометрического ряда однозначно определяется через его знаменатель и первый член: n₂=n₁φ; n₃= n₁φ²; n₄=n₁φ³ и т.д. Поэтому связь между предельными значениями членов ряда n₁=n_min и n_z=n_max и их числом z выражается зависимостью

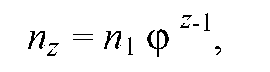
Для обеспечения требуемого диапазона регулирования R_n при заданном значении знаменателя φ привод должен иметь Z ступеней скорости число которых определяется зависимостью

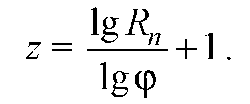
При проектировании приводов должны применяться стандартные значения знаменателя φ.

Выбор значения знаменателя геометрического ряда

Значения знаменателей φ геометрических рядов стандартизированы.Это обеспечивает нормализацию технических характеристик (частот вра­щения и двойных ходов, значений подач и других параметров), что позво­ляет упростить кинематические расчеты станков, осуществлять унифика­цию их деталей и узлов. Стандартные значения знаменателей геометриче­ских рядов установлены исходя из условий десятичной и двоичной повто­ряемости значений членов любого ряда.

Десятичная повторяемость определена стандартом на предпочтительные числа и ряды предпочтительных чисел. Определим знаменатель ряда при этом условии.

Имеем геометрический ряд: n₁, n₂, n₃,..n_x,..n_p,..n_y,..n_q,..n_z.

По условию десятичной повторяемости n_q=n_pφ^E₂ , где Е₂ - целое число, равное числу ступеней в каждом десятичном интервале. Следовательно,

Двоичная повторяемость обусловлена необходимостью применения многоскоростных электродвигателей, частота вращения которых при пере­ключении изменяется в два раза, например, n_э = 750/1500/3000 мин^-1. Аналогично, условие двойной повторяемости выполняется, если

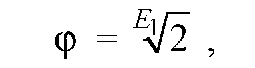
где Е₁ - целое число, равное числу ступеней скорости в каждом двойном интервале.

Арифметический ряд подач

Некоторые схемы обработки резанием с возвратно-поступательным главным движением (строгание, долбление) основаны на периодическом движении подачи. На станке она осуществляется с помощью механизма дискретного действия, обычно храпового. Величина подачи в этом случае прямо пропорциональна углу поворота храпового колеса, зависящему от числа зубьев, на которое оно периодически поворачивается.

При каждом повороте храпового колеса на угол между зубьями подача изменяется на одну и ту же величину. Поэтому последовательность значений подачи образует арифметический ряд

S_1,S_2,S₃,…S_i,…S_z-1,S_z

где s₁ = s_min - значение подачи, соответствующее повороту храпового колеса на 1 зуб;s2 - значение подачи, соответствующее повороту храпового колеса на 2 зуба и т. д.;s_z - максимальное значение подачи.

При этом s₂ - s₁ = s_i+1 – S_i = C - разность арифметического ряда. Для арифметического ряда с z членами справедливы следующие соотношения:

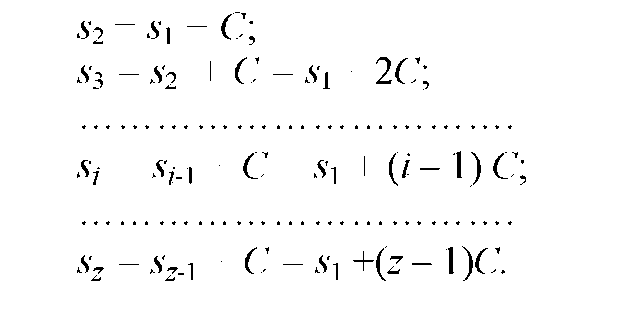
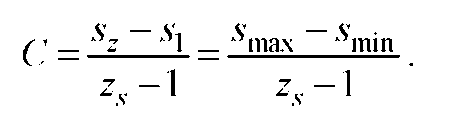
Следовательно,

При заданных разности С арифметического ряда и предельных значениях подачи S_min и s_max определяется число подач z_s, которое должен обеспечить проектируемый привод:

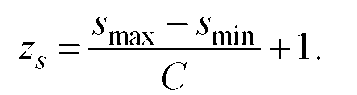
В отдельных случаях, обычно при небольшом числе значений подачи, арифметический ряд применяется и для задания величины непрерывной подачи. Например, значения подачи, создаваемые кинематикой вертикально-сверлильного станка модели 2Н125Л, составляют арифметический ряд с разностью С = 0,1 мм/об. Арифметический ряд используется также при проектировании винторезных цепей резьбообрабатывающих станков, если значения шага нарезаемой резьбы образуют арифметический ряд.