22.Определение числа зубьев колес групповых передач.

Прямозубые колеса. Обычно модули всех передач группы одинаковы. В этом случае z_j + z′_j = S_z = const (1)где z_j, z′_j – числа зубьев соответственно ведущего и ведомого колес j-той пары, j = 1, 2 …p; S_z – сумма чисел зубьев обоих колес. Передаточное отношение этой пары колес i_j = z_j / z′_j. (2)

Из уравнений (1) и (2) следует

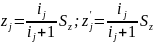
По этим формулам определяют числа зубьев всех колес группы при заданном значении S_z. Если оно неизвестно, то в общем случае S_z может быть определено методом наименьшего кратного. Для этого, представив i_j = a_j / b_j, где a_j и b_j – взаимно простые числа, получим:

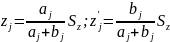(3)

Числа z_j и z′_j будут целыми, если величина S_z кратна сумме a_j + b_j.

Для группы, содержащей p передач, наименьшая сумма зубьев S_zmin равна наименьшему общему кратному K сумм a₁ + b₁, a₂ + b₂, …, a_p + b_p, т.е. S_zmin = K. По найденному значению S_zmin, пользуясь зависимостями (3), определяют минимальное число зубьев малого колеса z _jmin или z’ _jmin .

Минимальное число зубьев определяют в понижающих передачах для ведущего колеса передачи с минимальным передаточным отношением,а в повышающих передачах – для ведомого колеса передачи с максимальным передаточным отношением. Если найденное таким образом минимальное число зубьев меньше допускаемого значения [z_min], то его увеличивают в Е число раз, где

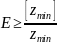
С учетом Е сумма чисел зубьев S_z рассматриваемой группы составит

S_z = E S_{z min} = EК.

Расчет суммы S_z и чисел зубьев колес производится для каждой группы в отдельности.

Для уменьшения материалоемкости колес понижающие и повышающие передачи последней в порядке переключения группы иногда выполняют с разными модулями. Сумма чисел зубьев таких передач различна. Ее выражают через значения межосевого расстояния А и модуля m_j рассматриваемой передачи.

Так как 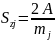, то

Числа z_j и z′_j будут целыми, если 2А = Еm_j(a_j + b_j), где Е – целое число. Поэтому наименьшее удвоенное межосевое расстояние принимают

равным наименьшему кратному произведений m_j(a_j+ b_j). Если оно получается значительным по величине, то находят наименьшее общее кратное модулей передач группы и, увеличив его в некоторое число раз, принимают полученное число за удвоенное межосевое расстояние. В этом случае значения S_z получаются целыми, а z_j и z′_j – дробными числами. Последние

округляют, сохраняя расчетное значение S_z.

Косозубые колеса. Для группы передач с косозубыми колесами с одинаковым нормальным модулем m_н межосевое расстояние А у всех передач одинаково:

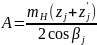
где β_j – угол наклона зубьев, который может быть одинаковым или разным у отдельных передач. На основании зависимостей числа зубьев сопряженных колес в общем случае

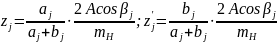
Возможны два варианта:

1. Все колеса группы имеют одинаковый угол наклона, т.е. β_i = β =const. В этом случае сумму S_z чисел зубьев колес находят как величину,кратную суммам a_j + b_j, и по ней определяют межосевое расстояние и числа зубьев колес:

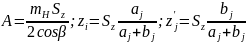
2. Задано межосевое расстояние А. Тогда находят K – наименьшее кратное сумм a_j + b_j. Для каждой передачи группы принимают соответствующую сумму чисел зубьев S_zj = KЕ_j, задавая целое число E_j так, чтобы угол наклона зубьев не превышал рекомендуемых значений. Числа зубьев сопряженных колес: