17. Проектирование кинематики привода со сложенной структурой

Структура, представляющая собой со­единение нескольких (обычно не более двух) простых множительных структур, называется сложенной. В этом случае число ступеней zскорости равно сумме чисел ступеней скоро­сти первой z₁и второй z₂составляющих струк­тур. Для упрощения конструкции привода со­ставляющие структуры, как правило, имеют общую часть, обеспечивающую z₀ступеней скорости, тогда 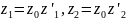Поэтому 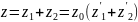Общая часть является основной и служит для получения всех ступеней скорости выходного звена привода. Структуры, обеспечивающие z₁и z₂ ступеней скорости, называются дополнительными и используются для полу­чения только части ступеней скорости выходного звена: первая с более низ­кими, а другая с более высокими значениями частоты вращения. На практике часто применяется вариант сложенной структуры привода, когда структуры, создающие z₀и z₁ступеней скорости, совпадают. В этом случае где я_д- число ступеней скорости, создаваемых дополнительной структурой.Объединение составляющих структур в сложенную структуру осуществ­ляется с помощью переключаемых зубчатых передач или муфт. Например, z₀ ступеней скорости, относящихся к верхней области диапазона регулиро­вания и создаваемых основной структурой, передаются на шпиндель IV при смещении колеса 9 влево и зацеплении кулачковой муфты. Нижняя область регулирования скорости привода обеспечивается по­следовательным соединением основной z₀и дополнительной z_дструктур и подключением последней к шпинделю через передачу z₈- z₉. Такой способ построения сложенной структуры характерен, в частности, для приводов главного движения универсальных токарно-винторезных станков. Для построения структурной сетки сложенного привода необходимо определить характеристики групп передач и составить формулу структуры привода. Характеристики групп основной структуры определяются так же, как и для обычной множительной структуры. Характеристика любой груп­пы дополнительной структуры равна произведению числа скоростей z₀ос­новной структуры и числа ступеней скорости, создаваемых предшествую­щими группами дополнительной структуры. Например, если z₀= р₁р₂, г_д = р₃р₄, причем р₁= р_о= 2, р₂= р₁ = 3, р₃= р_II = 2, р₄= р_III = 2, то x₁ = 1, x₂= 2, х₃= z₀ = 2 ∙ 3 = 6, x₄= 2 ∙ z₀ = 2 ∙ 6 = 12, то структурная формула привода имеет вид z= 2(1)3(2)[1 + 2(6) ∙ 2(12)]. Для z= 12 предпочтителен вариант сложенной структуры, выражаемой формулой z= 6 [1+11]. В этом случае структурная формула привода имеет вид: z= 3(1)2(3)[1+1 ∙ 1]. Особенностью построения структурной сетки сложенного привода является то, что вначале строятся сетки для составляющих структур затем - совмещенная структурная сетка, а по ней график частот вращения. Так как основная и дополнительная структуры сложенного привода являются простыми множительными, то структурные сетки для них строятся по общей методике.

18. Проектирование кинематики привода со ступенью возврата

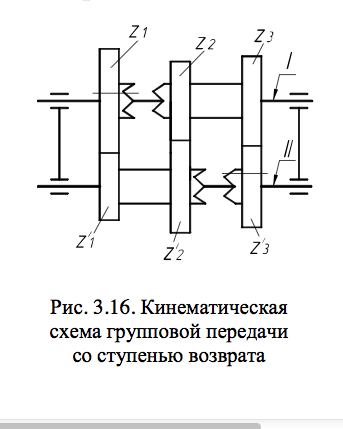Группа со ступенью возврата устанавливается обычно в приводах подач. Такая группа имеет диапазон регулирования, превышающий допускаемое его значение для простой множительнойгруппы, и позволяет уменьшить количество колес в коробке за счет использования некоторых зубчатых зацеплений для передачи движения в двух направлениях.

Рассмотрим в качестве примера группу с тремя передачами (рис. 3.16), обеспечивающую четыре различных передаточных отношения:

i₁ = (z/z'₁)×(z’₂/z₂)×(z₃/z'₁); i₂ = z₁/z'₁; i₃ = z₂/z'₂; i₄ = z₃/z'₃

Учитывая, что ряд частот вращения должен быть геометрическим, уравнение настройки для данной группы имеет вид

i₁:i₂:i₃:i₄ =1:φ^x :φ^2x:φ^3x. (3.67)

Предельные значения передаточных отношений i₄ и i₂ группы должны удовлетворять условию i₄ / i₂ ≤ [R_p].

Из уравнения (3.67) i₄ / i₂ = φ^2x. Тогдаx≤ (lg[R_p])/2lgφ.(3.68)

Приняв i₂ = 1/φ_u , получим i₃ =φ^x-u; i₄ =φ^2x-u; i₁ = 1/φ^x+u(3.69)

При кинематическом расчете группа со ступенью возврата принимается чаще как переборная с характеристикой x и четырьмя передаточными отношениями.

Пример. Определить передаточные отношения передач привода со ступенью возврата по исходным данным: предельные значения частоты вращения ведомого вала – n_min = 25 мин^-1; n_max = 1080 мин^-1; частота вращения электродвигателя n_э = 1440 мин^-1; знаменатель ряд частот вращенияφ = 1,41; максимальное значение диапазона регулирования группы [R_p] = 8.

Диапазон регулирования привода R_n = n_max/n_min = 1080 = 43, 2 ; число

ступеней скорости z = lgR_n/lgφ+1= lg43,2/lg1,41+1=11,8. Принимаем z = 12.

Для φ = 1,41 в соответствии с (3.68) характеристика группы со ступенью возврата x=lg[R_p]/2lgφ=lg8/2lgφ=3

Тогда формула структуры данного привода z = 12 = 3(1)⋅4(3). Таким образом, привод содержит две групповые передачи – обычную и со ступенью возврата. передаточные отношения передач привода определяем аналитическим методом. С учетом исходных данных стандартные значения частот вращения составляют следующийгеометрический ряд: 22,4 – 31 – 45 – 63 – 90 – 125 – 180 – 250 – 355 – 500 – 710 – 1000 (мин^-1).

Следовательно, минимальное передаточное отношение привода 1 i_min=n₁/n_э=22,4/1440или выраженное через заданное значение φ: i_min=1/φ^q=1/1,41^12,1 т.е. q=12,1 Такое передаточное отношение не может быть обеспечено только двумя групповыми передачами, поэтому привод должен содержать одиночную передачу, например, зубчатую с передаточным отношением i₀ (рис. 3.17, а).

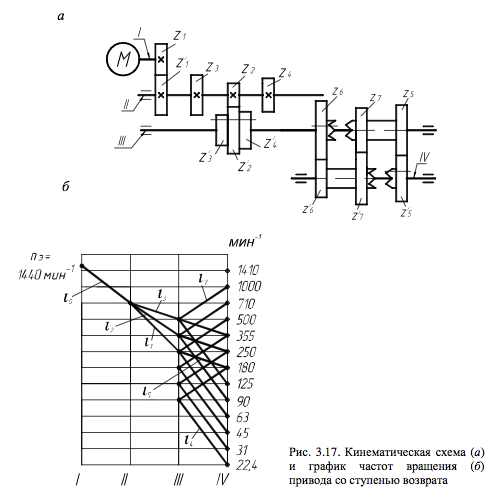
Примем: i4 = z₅/z’₅ = 1/1,41⁴ = 1/4, u = 4. Тогда, на основании (3.69), для группы со ступенью возврата имеем:

i₅ = (z₆/z'₆)×(z’₇/z₇)×(z₅/z'₅)=1/φ^u+x=1/1,41⁴⁺³=1/1,41⁷;

i₆ = z₆/z'₆=φ^u-x=1,41^4-3-1/1,41;

i₇ = z₇/z'₇=φ^2u-x=1,41^2×4-3-1/1,41²=2;

Минимальное передаточное отношение i = z₂/z’₂восновной группе

примемравным 1/φ ^к= 1,41³.

Тогдаi₂=z₃/z’₃=1/1,41² =1/2; i₃=z₄/z'₄= 1/1,41 .

Передаточное отношение одиночной передачи i₀=z₁/z'₁= 1/φ ^l

где l=q–к–u–x =12,1–3–7=2,1 т.е. i₀ =1/1,41^2,1

График частот вращения валов данного привода приведен на рис.3.17, б.