15. Проектирование кинематики привода с многоскоростным приводом.

В приводах главного движения и подач металлорежущих станков, кроме односкоростных, часто применяются также многоскоростные двигатели переменного тока со ступенчатым изменением частоты вращения.Для обеспечения стандартного геометрического ряда частот вращения(чисел двойных ходов подач) можно применять только двигатели, частотавращения которых при их переключении изменяется в 2 раза, например, 750/1500; 1500/3000; 750/1500/3000 мин^-1, т.е. образует ряд с φ_э= 2.

Многоскоростной электродвигатель заменяет одну группу передач шестеренчатой скорости, поэтому его рассматривают как фиктивную группу или «электрогруппу» с числом передач p_э, равным числу его скоростей, и характеристикой x_э. Так как

φ_э= 2 =φ_х, то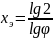

Структурная формула привода с многоскоростным двигателем имеет видz = p_э(x_э)p₁(x₁)p₂(x₂) …p_m(x_m).

Общее число ступеней скорости привода с многоскоростным электродвигателем z = p_эz_к, где z_к – число ступеней скорости шестеренчатой коробки. Следовательно, применение такого двигателя упрощает механическую часть привода. Однако многоскоростной двигатель дороже, и его выбор должен быть обоснован экономически.

Для каждого из стандартных значений φхарактеристика x_э

имеет определенное значение, поэтому порядок переключения электрогруппы зависит от φ(табл. 3.1).

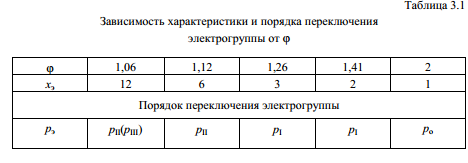
При φ= 1,58 и φ= 1,78 характеристика x_эвыражается дробным числом, что не позволяет использовать многоскоростные двигатели. Применение многоскоростных двигателей накладывает следующиеограничения на структуру привода: – электрогруппа, являясь источником энергии, в порядке расположения всегда является первой, т.е. p_э= p₁;

– порядок переключения электрогруппы(p₀, p_Ιи т.д.) зависит от значенияφ;

– число передач в группах, предшествующих электрогруппе, также зависит от φ.

16. Особенности проектирования кинематики привода с перекрытием ступеней скорости

Перекрытие ступеней̆ скорости привода имеет место, если одно и то же значение частоты вращения шпинделя обеспечивается разными кинематическими цепями. Перекрытие применяется, когда расчетное значение числа ступеней скорости z нельзя представить в виде произведения чисел 2 и 3, например, если z = 11, z = 17 и т.п. В этом случае проектирование ведется на основе базовой̆ структуры, для определения которой̆ задаются фиктивным числом z_ф ступеней скорости. Это число должно быть кратно числам 2 и (или) 3 и превышать требуемое значение z. Например, если z = 10, то z_ф = 12.

Перекрытие достигается за счет уменьшения характеристик групповых передач. Практически оно осуществляется за счет уменьшения характеристики последней в порядке переключения группы передач базовой структуры на величину ∆x, что позволяет уменьшить диапазон регулирования этой группы, превышающий значения диапазонов регулирования других групповых передач.

При проектировании кинематики привода с перекрытием ступеней скорости требуется определить величину ∆x для конкретного значения ∆z, равного z_ф - z. Рассмотрим эту задачу. Используемые данные приведены в табл. 1.

Расчетные величины	Значения расчетных величин
	для проектируемой структуры	для базовой структуры
Число ступеней скорости привода Характеристика последней переборной группы Общий диапазон регулирования привода Диапазон регулирования последней переборной группы Диапазон регулирования остальных групп	z x Rn = φ (z−1) Rp = φ (p−1)x Rx	zф xф Rnф = φ(zф−1) Rpф = φ(p−1)xф Rx

Учитывая, что z_ф - z = ∆z, а x_ф - x = ∆x, из (3) следует равенство ∆ z = (р-1)∆x, откуда получаем зависимость для определения искомого значения ∆x

Так как общий̆ диапазон регулирования R_n = R_x⋅R_p , то аналогично для базовой̆ структуры R_nф = R_x⋅R_pф .

R_n =φ^(z−1) =R_x φ^(p−1)x (1)

R_nф = φ^{(z φ −1)} =R_x φ^(p−1)xф . (2)

Разделив (2) на (1), имеем

φ^(zф−z) = φ^{(p−1)(xф−x).} (3)

∆x = ∆z / p−1 (4)

На основании изложенного проектирование кинематики привода с перекрытием значений скорости рекомендуется выполнять в следующей̆ последовательности:

1) задаться фиктивным значением z_ф, которое больше заданного z и может быть представлено в виде произведений чисел 2 и (или) 3;

2) составить формулу базовой структуры привода для принятого фиктивного значения z_ф:

z_ф = р₁(x₁)p₂(x₂)...p_m(x_mф); (5)

3) определить ∆z = z_ф - z и по формуле (4) – величину ∆x;

4) определить фактическое значение характеристики последней̆ переборной̆ группы проектируемого привода: x_m = x_mф - ∆x;

5) составить формулу структуры привода:

z = р₁(x1)p₂(x₂)...p_m(x_m); (6)

6) построить структурную сетку проектируемого привода.

Особенности структуры привода с неравномерным рядом частот вращения

Расширение диапазона регулирования привода без усложнения его конструкции (введения дополнительной группы передач или применения ступени возврата) обеспечивают структуры с неравномерным («ломаным») геометрическим рядом частот вращения ведомого вала. Такой ряд получается за счет увеличения характеристик групповых передач по сравнению с их значениями для стандартного геометрического ряда.

Неравномерность значений ряда может быть достигнута на различных его участках. Для приводов станков экономически целесообразно создавать неравномерность ряда за счет увеличения значений его знаменателя в начале и в конце ряда частот вращения по сравнению со значением знаменателя на среднем участке ряда. Практически такая неравномерность достигается путем увеличения характеристики первых в порядке переключения групп.

Рассмотрим в качестве примера привод, структура которого выражается формулой̆ z = 3(2)2(5)2(6). Она получена на основе базовой̆ структуры z = 3(1)2(3)2(6), обеспечивающей стандартный геометрический ряд частот вращения, путем увеличения в ней характеристик основной и первой переборной групп, со- ответственно до 2 и 5.

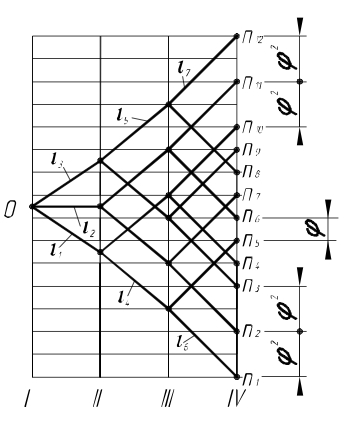Структурная сетка привода с модифицированной таким образом структурой показана на рис. 1. Создаваемые данной структурой̆ значения частот вращения ведомого вала в диапазоне от n₃ до n₁₀ образуют геометрический ряд со знаменателем, равным φ, а на крайних участках от n₁ до n₃ иот n₁₀ до n₁₂ – со знаменателем, равным φ² .

Таким образом, в целом геометрический ряд частот вращения является неравномерным, однако такая неравномерность практически оправдана благодаря тому, что станок преимущественно эксплуатируется при средних значениях частоты вращения шпинделя, тогда как крайние ее значения используются значительно реже.

Существенным преимуществом рассмотренной структуры является значительное увеличение диапазона регулирования привода.

Следует отметить, что более чем двукратное увеличение диапазона регулирования привода достигается без усложнения конструкции коробки скоростей при том же количестве валов и зубчатых передач