
- •Предисловие
- •Содержание
- •Глава1……………………………………………………………….
- •Глава 2
- •Глава 3. Действительные числа
- •Введение
- •Глава 1.
- •1.1. Расширение понятия числа
- •1.2. История возникновения и развития понятия «рационального числа»
- •1.3. Понятие дроби
- •1.4. Отношение равенства дробей Определение 6. Две дроби и называют равными, если
- •1.5. Приведение дробей к общему знаменателю
- •1.6. Действия с дробями
- •Вопросы для самопроверки
- •Задания для самопроверки
- •Глава 2. Множество положительных рациональных чисел
- •2.1. Понятие положительного рационального числа
- •Вопросы для самопроверки
- •2.2. Отношения на множестве
- •2.2.1. Отношение равенства
- •2.2.2. Отношение «меньше»
- •2.2.3. Свойства отношения «меньше»
- •2.2.4. Отношение больше на множестве
- •Вопросы для самопроверки
- •2.5. Операции на множестве
- •2.5.1. Операция сложения на
- •2.6. Свойства операции сложения на
- •Вопросы для самопроверки
- •2.6.2. Вычитание на
- •2.8. Свойства операции вычитания
- •Вопросы для самопроверки
- •2.6.3. Умножение положительных рациональных чисел
- •2.10. Свойства операции умножения
- •Вопросы для самопроверки
- •2.11. Деление положительных рациональных чисел
- •2.11. Свойства операции деления
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Решение арифметических задач с дробями
- •Задачи на отыскание дроби от заданного числа
- •Задачи на отыскание числа по заданной величине, по дроби
- •Задачи на отыскание дроби от заданного числа и числа по заданной величине
- •Задачи на совместную работу
- •Задачи на движение
- •2.12. Десятичные дроби
- •2.13. Операции над десятичными дробями
- •2.14. Преобразование обыкновенных дробей в десятичные
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Задачи на проценты
- •Задания для самостоятельного решения
- •Глава 3. Действительные числа
- •3.1. Бесконечные дроби
- •3.2. Понятие иррационального числа
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Примеры и задачи на все действия с обыкновенными и десятичными дробями
- •Понятие действительного числа
- •3.3. Отношение порядка на множестве
- •3.4. Свойства множества
- •3.5. Арифметические операции на
- •Вопросы для самопроверки
- •3.6. Аксиоматическое построение множества
- •3.7. Множество
- •3.8. Арифметические операции на множестве
- •3.9. Алгебраические и трансцендентные числа
- •Вопросы для самопроверки
- •3.10. Приближенные вычисления
- •3.11. Округление чисел
- •Вопросы для самопроверки
- •Литература
1.5. Приведение дробей к общему знаменателю
Определение 10. Приведением дробей к общему знаменателю называют замену дробей равносильными дробями, имеющими одинаковые знаменатели.
Теорема 5. Любые две дроби можно привести к общему знаменателю.
Доказательство.
Пусть
![]() и
и
![]() − произвольные дроби.
− произвольные дроби.
Умножим
числитель и знаменатель первой дроби
на
![]() ,
а второй на
,
а второй на
![]() имеем дроби с одинаковыми знаменателями:
имеем дроби с одинаковыми знаменателями:
![]() В силу транзитивности отношения
равносильности дробей, имеем:
В силу транзитивности отношения
равносильности дробей, имеем:
![]() Теорема доказана.
Теорема доказана.
В
силу коммутативности умножения на
множестве натуральных чисел:
![]() По теореме
3, имеем
По теореме
3, имеем
![]()
Отметим,
что общим знаменателем двух дробей
и
является общее кратное чисел
и
![]() а наименьшим общим знаменателем
а наименьшим общим знаменателем
![]()
Алгоритм приведения дробей к общему знаменателю:
− найти НОК знаменателей дробей;
− найти дополнительные множители, разделив НОК на любой знаменатель;
− умножить числитель и знаменатель любой дроби на соответствующий дополнительный множитель.
Пример.
Привести
дроби
![]() и
и
![]() к наименьшему общему знаменателю.
к наименьшему общему знаменателю.
Решение.
НОК(24;36)=72;
72:24=3, 72:36=2;
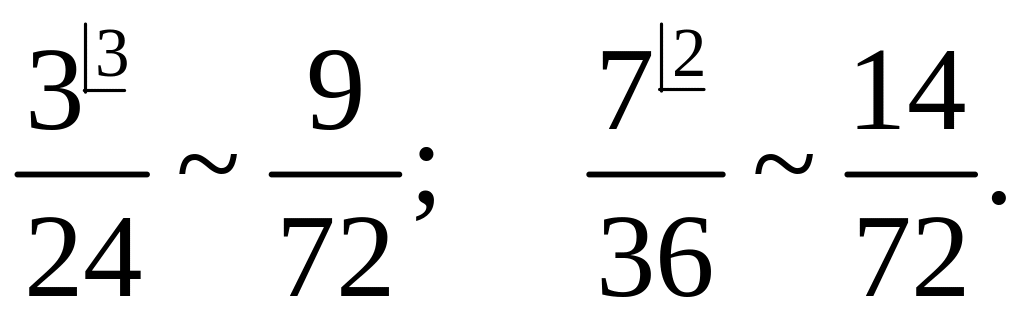
Определение 11. Смешанной дробью называют число, имеющее целую и дробную части.
Пример.
![]() .
.
Теорема
6. Любая
дробь
единственным образом представима в
виде
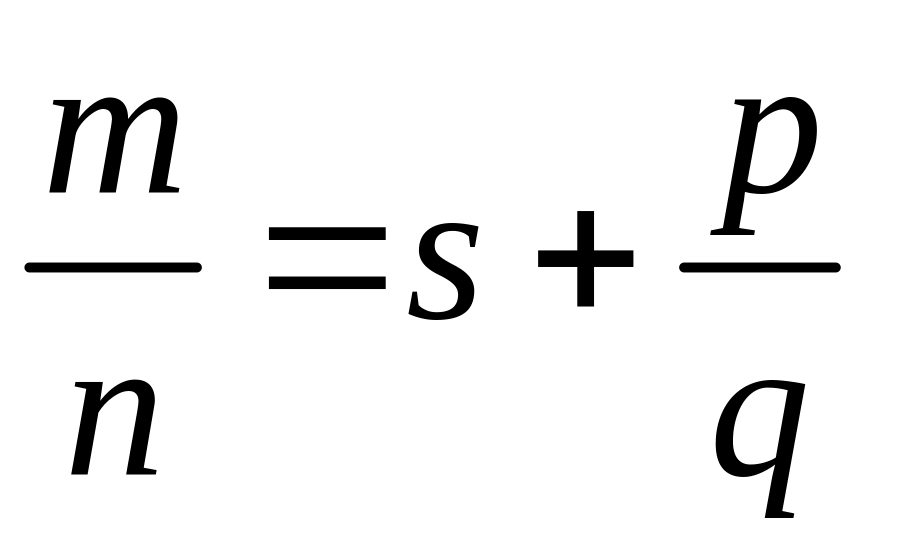 ,
где
,
где
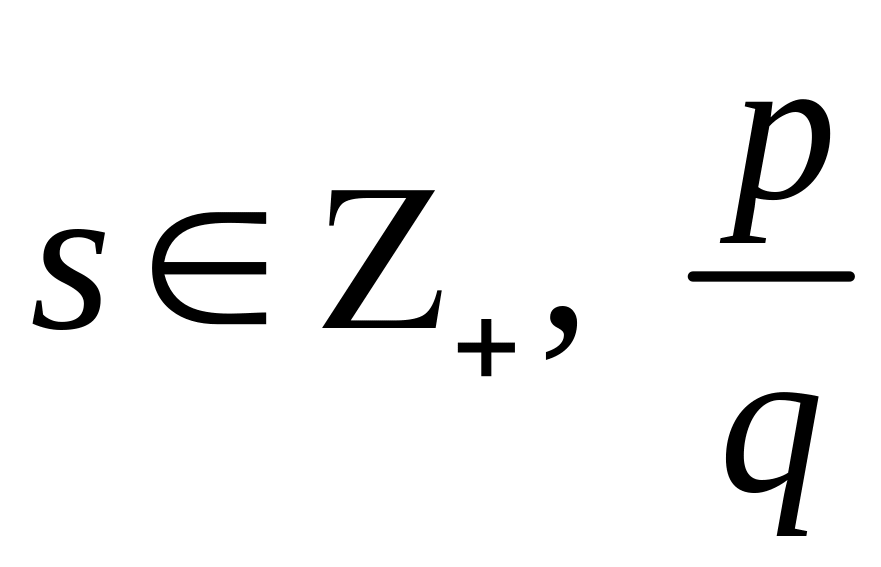 − правильная несократимая дробь, то
есть
− правильная несократимая дробь, то
есть
![]()
![]()
Доказательство.
Существование. Разделим
![]() с остатком на
с остатком на
![]() ,
имеем
,
имеем
![]() Тогда
Тогда
![]() Пусть
Пусть
![]() тогда
тогда
![]() где
Сокращая дробь
где
Сокращая дробь
![]() на
на
![]() ,
получим
,
получим
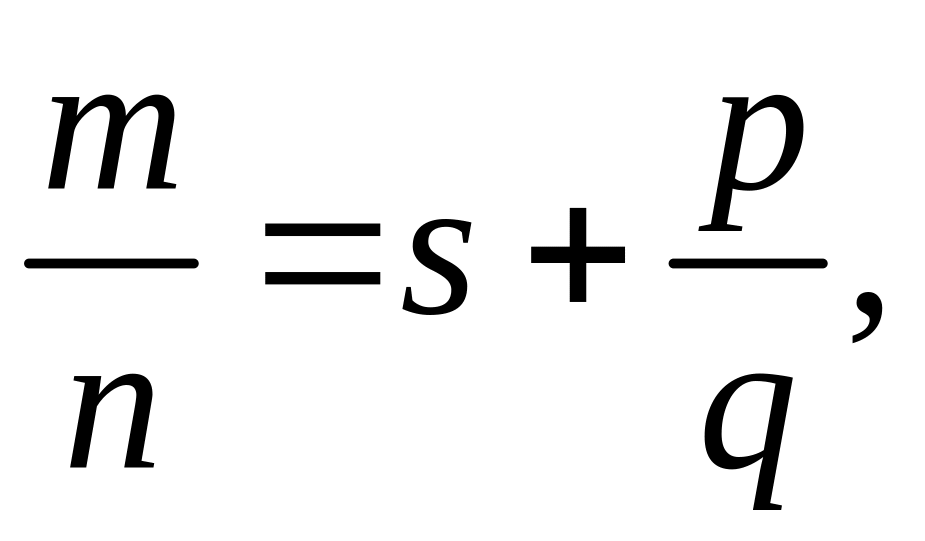 что и дает требуемое представление.
что и дает требуемое представление.
Единственность.
Докажем
методом «от противного». Пусть
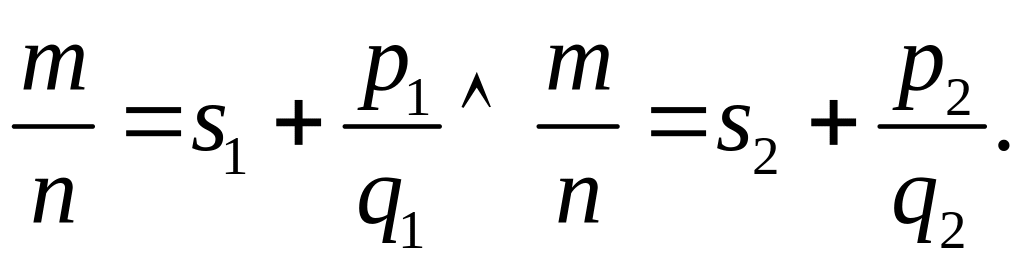
При
этом
![]()
![]()
![]()
![]()
Тогда,
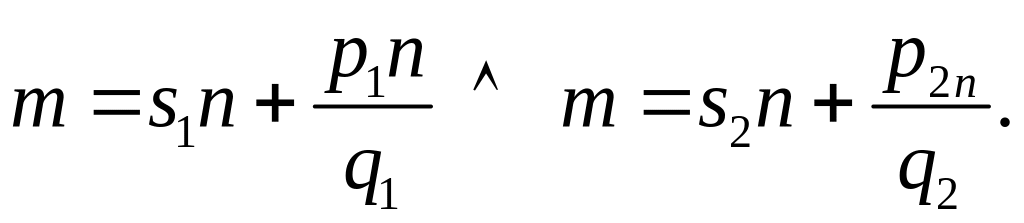
Так
как
![]() ,
то
,
то
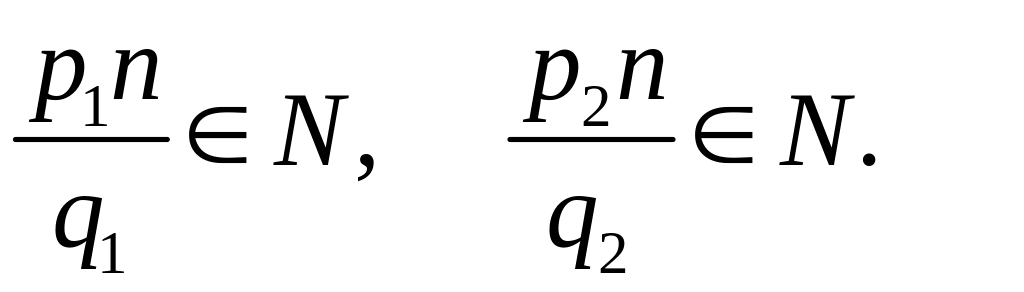
В
силу единственности деления с остатком
можем записать равенства:
![]() и
и
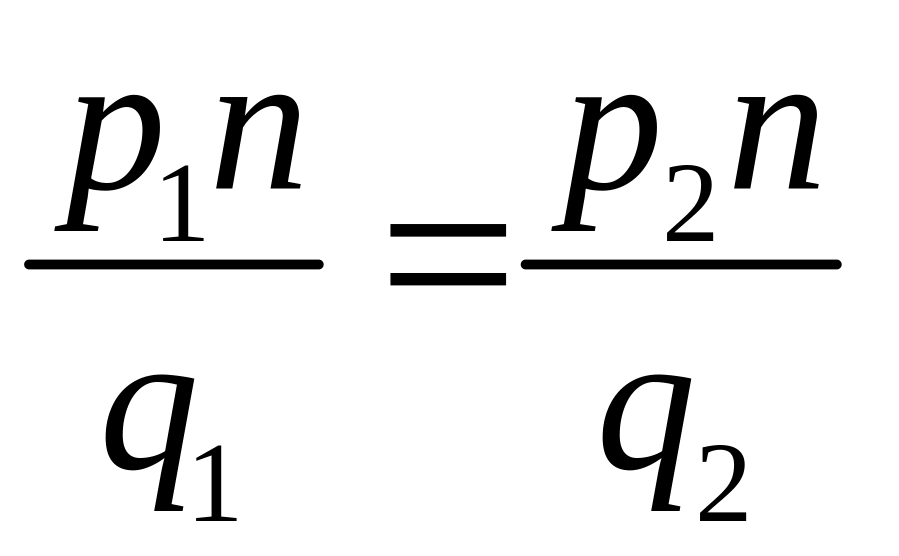 или
или
![]() и
и
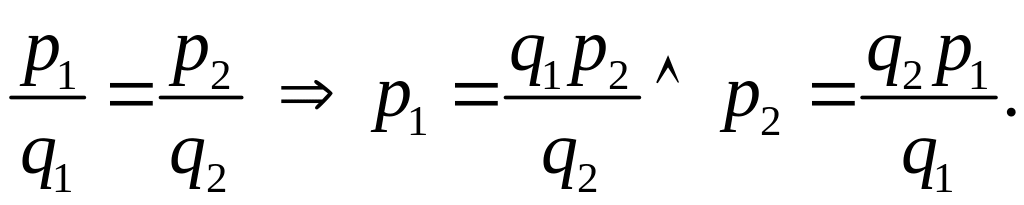
Так
как
![]() и
и
![]() то
то
![]() и
и
![]() .
Деление возможно, только при условии
.
Деление возможно, только при условии
![]() Отсюда имеем
Отсюда имеем
![]() Итак, установлено, что
Итак, установлено, что
![]()
![]() и
Таким образом единственность доказана.
и
Таким образом единственность доказана.
Теорема доказана.
1.6. Действия с дробями
Сумма, разность, частное и произведение двух дробей вычисляются по правилам:
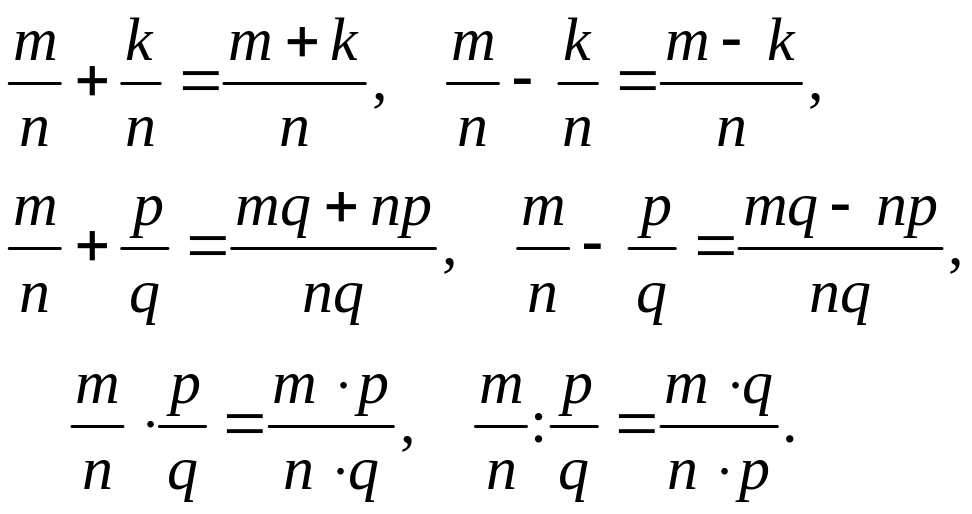
Вопросы для самопроверки
Обоснуйте необходимость расширения множества
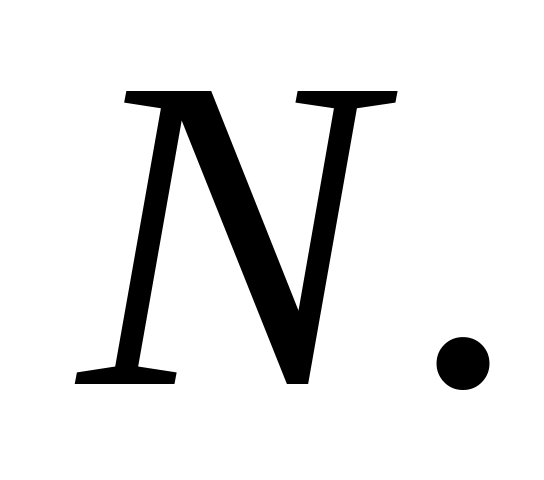
Дайте определение дроби. Приведите примеры дробей.
Сформулируйте определение равных дробей. Приведите примеры равных дробей.
Докажите теорему о том, что отношение равенства дробей является отношением эквивалентности.
Сформулируйте определение равносильных дробей.
Следует ли из равенства дробей их равносильность? Следует ли из равносильности дробей их равенство? Приведите примеры равносильных, но не равных дробей.
Докажите теорему о том, что отношение равносильности дробей является отношением эквивалентности.
Сформулируйте определение смешанной дроби.
Сформулируйте определение аликвотной дроби (доли).
Сформулируйте определение неправильной дроби. Сформулируйте определение правильной дроби. Приведите примеры.
Сформулируйте определение несократимой дроби.
Сформулируйте основное свойство дроби.
Что называют сокращением дробей?
Что называют приведением дробей к общему знаменателю.
Сформулируйте алгоритм приведения дробей к общему знаменателю.
Сформулируйте правила сравнения дробей.
Сформулируйте правила действий с дробями.
