
- •Предисловие
- •Содержание
- •Глава1……………………………………………………………….
- •Глава 2
- •Глава 3. Действительные числа
- •Введение
- •Глава 1.
- •1.1. Расширение понятия числа
- •1.2. История возникновения и развития понятия «рационального числа»
- •1.3. Понятие дроби
- •1.4. Отношение равенства дробей Определение 6. Две дроби и называют равными, если
- •1.5. Приведение дробей к общему знаменателю
- •1.6. Действия с дробями
- •Вопросы для самопроверки
- •Задания для самопроверки
- •Глава 2. Множество положительных рациональных чисел
- •2.1. Понятие положительного рационального числа
- •Вопросы для самопроверки
- •2.2. Отношения на множестве
- •2.2.1. Отношение равенства
- •2.2.2. Отношение «меньше»
- •2.2.3. Свойства отношения «меньше»
- •2.2.4. Отношение больше на множестве
- •Вопросы для самопроверки
- •2.5. Операции на множестве
- •2.5.1. Операция сложения на
- •2.6. Свойства операции сложения на
- •Вопросы для самопроверки
- •2.6.2. Вычитание на
- •2.8. Свойства операции вычитания
- •Вопросы для самопроверки
- •2.6.3. Умножение положительных рациональных чисел
- •2.10. Свойства операции умножения
- •Вопросы для самопроверки
- •2.11. Деление положительных рациональных чисел
- •2.11. Свойства операции деления
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Решение арифметических задач с дробями
- •Задачи на отыскание дроби от заданного числа
- •Задачи на отыскание числа по заданной величине, по дроби
- •Задачи на отыскание дроби от заданного числа и числа по заданной величине
- •Задачи на совместную работу
- •Задачи на движение
- •2.12. Десятичные дроби
- •2.13. Операции над десятичными дробями
- •2.14. Преобразование обыкновенных дробей в десятичные
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Задачи на проценты
- •Задания для самостоятельного решения
- •Глава 3. Действительные числа
- •3.1. Бесконечные дроби
- •3.2. Понятие иррационального числа
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Примеры и задачи на все действия с обыкновенными и десятичными дробями
- •Понятие действительного числа
- •3.3. Отношение порядка на множестве
- •3.4. Свойства множества
- •3.5. Арифметические операции на
- •Вопросы для самопроверки
- •3.6. Аксиоматическое построение множества
- •3.7. Множество
- •3.8. Арифметические операции на множестве
- •3.9. Алгебраические и трансцендентные числа
- •Вопросы для самопроверки
- •3.10. Приближенные вычисления
- •3.11. Округление чисел
- •Вопросы для самопроверки
- •Литература
Вопросы для самопроверки
Что называют числом знаков числа? Что называют значащими цифрами приближенного числа? Являются ли нули, входящие в состав приближенного числа и служащие для обозначения его десятичных разрядов значащими цифрами?
Дайте понятие верных (точных) цифр приближенного числа.
Сформулируйте определение абсолютной погрешности приближенного числа . Приведите пример.
Сформулируйте определение относительной погрешности приближенного числа . Приведите пример.
Что называют округлением числа ?
Сформулируйте правила округления чисел.
Сократите выражение
 ,
если а>0.
,
если а>0.Сократите выражение
 ,
если а<0.
,
если а<0.Сократите дробь
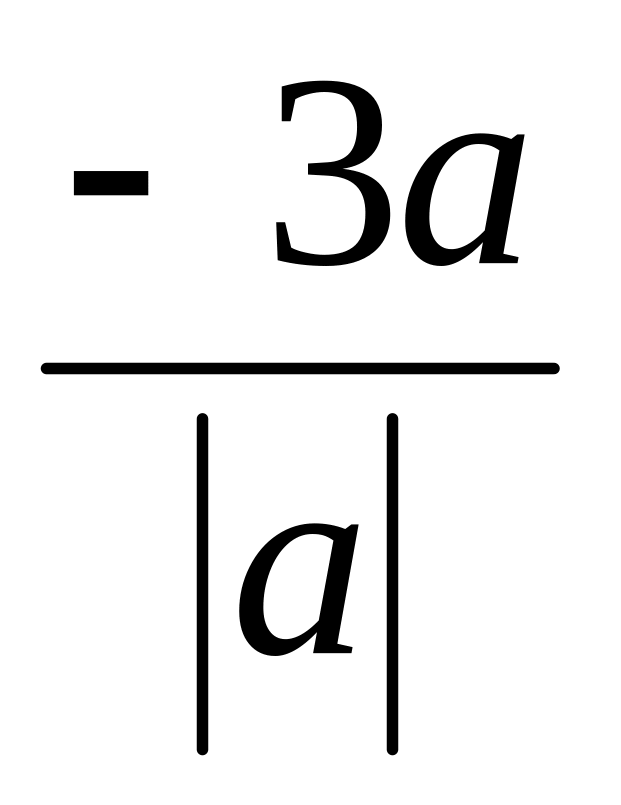 ,
если а<0.
,
если а<0.Сократите дробь
 .
.Найдите приближенное значение чисел по недостатку и по избытку с точностью до 0,001:

Найдите а+в; а–с; вс с точностью до
 ,
если
,
если

Найдите сумму, разность, произведение и частное чисел с точностью до
 ,
если
,
если

Найдите сумму, разность, произведение и частное чисел
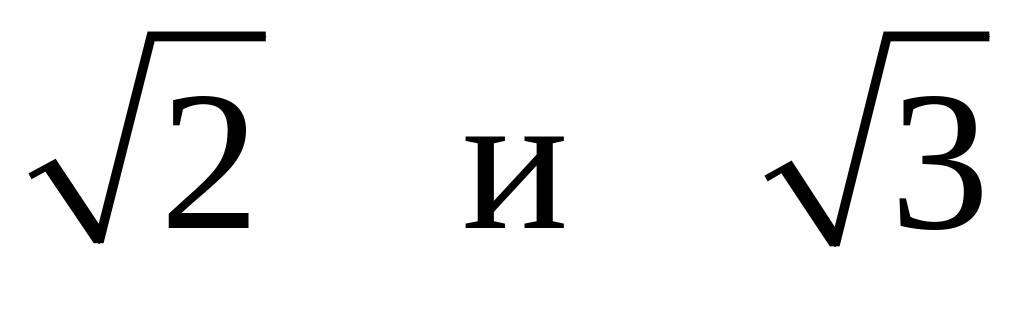 с точностью
до 0,01.
с точностью
до 0,01.Округлите числа до двух значащих цифр:
![]()
Округлите числа до трёх значащих цифр:
![]()
Округлите число 0,707906 до 1, 2, 3, 4 и 5 значащих цифр.
Округлите 4678 ц (до десятков); 6137,84 кг (до сотен); 4462,3 ц (до тысяч); 627 231 руб. (до тысяч).
Округлите число 11,07780 до десятых долей, до сотых долей, до тысячных долей, до целых.
Пользуясь правилом чётной цифры, округлить следующие числа:

Пользуясь правилом дополнения, написать с одним, двумя и тремя «верными» знаками следующие числа:
![]()
Значения чисел по недостатку и избытку равны: 82,5 кг и 83 кг; 0,075 и 0,076; 3,42 мм и 3,43 мм; 3 и 3,1; 4,5 и 4,6; 1,82 и 1,83. С какой точностью выражают они числа?
Определить число «верных» знаков следующих приближённых чисел: 17,05; 3,14; 0,0047; 2,0001; 5,0200; 0,03; 0,03000.
В результате измерения получены два приближенных числа 2,7 м и 2,62 м, которые требуется сложить. Укажите верные цифры в полученной сумме.
Сложить приближённые числа 60,4; 2,02; 0,222 и 0,0462. Укажите верные цифры в полученной сумме. Как можно было более рационально выполнить сложение?
Вычислить сумму, разность, произведение и частное чисел, считая, что слагаемые даны с точностью до десятых долей:
![]()
![]()
![]()
![]()
В комнате, длина которой равна ≈4,6 м, а ширина ≈3,8 м, нужно сменить плинтусы. Сколько погонных метров плинтуса для этого требуется?
Участок сада прямоугольной формы длиной ≈18,5 м и шириной ≈24,7 м нужно огородить изгородью. Какова её длина?
Бутылка с растительным маслом весит 1,350 кг. Каков вес масла, если пустая бутылка весит 0,545 кг?
Вес станка ≈0,48 т, вес подставки к нему ≈0,75 т. Для перевозки их подали автомашину грузоподъёмностью 2,0 т. Какого веса груз можно положить до полного использования грузоподъёмности автомашины?
Сколько значащих цифр имеет каждое из чисел: 794; 105,3; 0,43; 0,705; 0,045; 81,20; 0,630; 0,0080.
Округлить до четырёх верных значащих цифр числа: 15,7056; 2,3415; 0,36625; 0,02374.
Указать разницу в записях: «длина авторучки 14 см» и «длина авторучки 14,0 см».
Измерьте длину и ширину своей тетради по арифметике сантиметровой линейкой. Сколько значащих цифр в каждом из полученных приближённых чисел?
Вычислите произведение
 ,
обратив дробные числа в десятичные
дроби и округлив сомножители до четырёх
верных значащих цифр. Вычислить точное
значение произведения.
,
обратив дробные числа в десятичные
дроби и округлив сомножители до четырёх
верных значащих цифр. Вычислить точное
значение произведения.
На земельном участке 30% площади занимает дом, 50% занимают хозяйственные постройки, остальные 8,25 м 2 заняты огородом. Сколько листов шифера потребуется, чтобы огородить данный земельный участок, если размер одного листа
 ?
?Комнату длиной ≈5,6 м, шириной ≈3,2 м и высотой ≈2,7 м требуется оклеить обоями (потолок и стены). Вычислить, сколько рулонов обоев необходимо приобрести, если в комнате имеется окно шириной 1,4 м и высотой 1 м и дверь шириной 0,8 м и высотой 1,9 м; 1 рулон
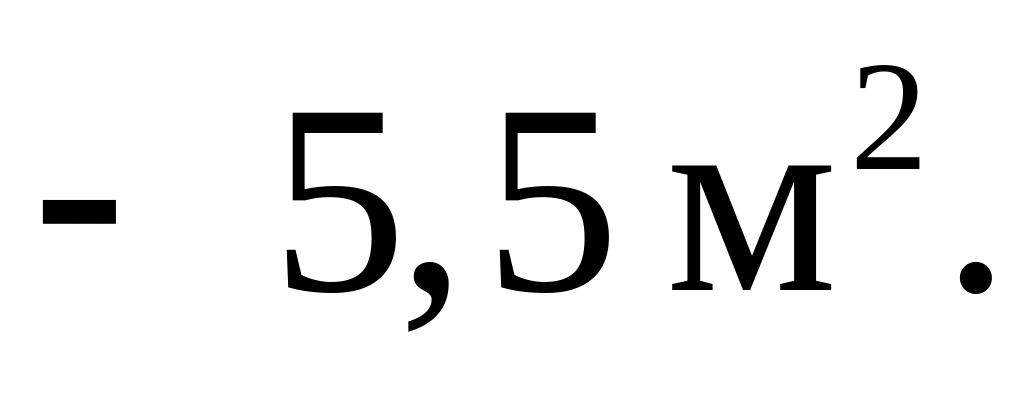
На окраску пола в комнате длиной 6,25 м и шириной 4,3 м пошло 2,75 кг краски. Сколько килограммов такой краски потребуется для окраски пола в комнате длиной ≈5,2 м и шириной ≈3,5 м?
Вычислить приближённое значение выражений, ограничиваясь точностью до 0,01:
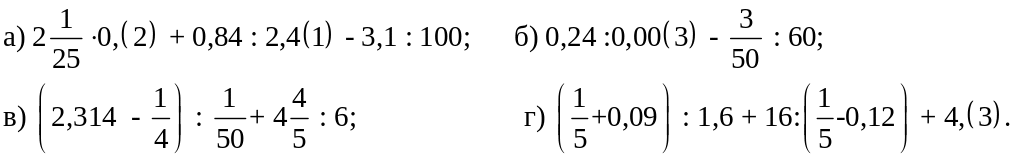
Выполните указанные действия, ограничиваясь точностью до 0,1:
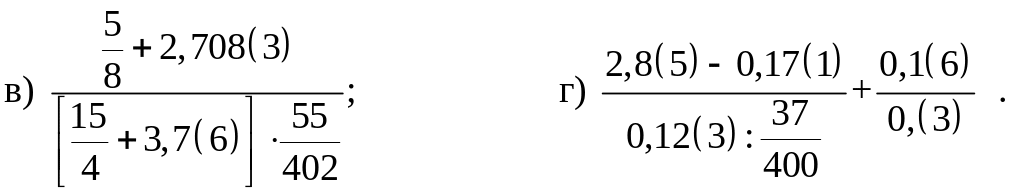
ЗАКЛЮЧЕНИЕ
Данное учебное пособие предназначено для студентов будущих учителей начальных классов ‒ и отражает опыт преподавания математики на факультете педагогики и методики начального образования Таганрогского государственного педагогического института.
Разделы «Рациональные числа» и «Действительные числа» необходимо рассматривать в вузовской программе не только с точки зрения широкого применения изучаемого материала в различных областях науки, в практической деятельности человека, но и как предмет, способствующий развитию математической и общекультурной составляющей будущего учителя.
Формирование профессиональной компетенции в области вероятностных знаний предполагает всестороннее изучение материала с глубоким научным обоснованием, так как знания не только гарантируют владение основными теоретическими фактами, но и способствуют формированию умения свободно оперировать материалом, стимулируют творческое отношение к приобретаемой профессии, способствуют формированию профессиональной самостоятельности будущего учителя начальных классов, его математической культуры.
Специфика текстовых задач и методов их решения требует от учителя определённого уровня математической подготовки. В первую очередь, ему необходимо знание основных фактов, положений, законов теории положительного рационального числа, а также умений решать задачи с их использованием. Основываясь на этих знаниях, учитель сможет не только быстро и правильно решать задачи, предлагаемые младшим школьникам, но и составлять их с учётом уровня подготовленности учащихся.
В системе профессиональной подготовки учителя для обучения математике младших школьников значительная роль отводится методике преподавания изучаемой дисциплины. В связи с этим возникает проблема формирования методической компетентности будущих учителей, способных к успешной реализации линии в школьном курсе математики.
