3.8. Арифметические операции на множестве

Определение 42. Модулем (абсолютной величиной) числа называют число, которое определяется следующим образом: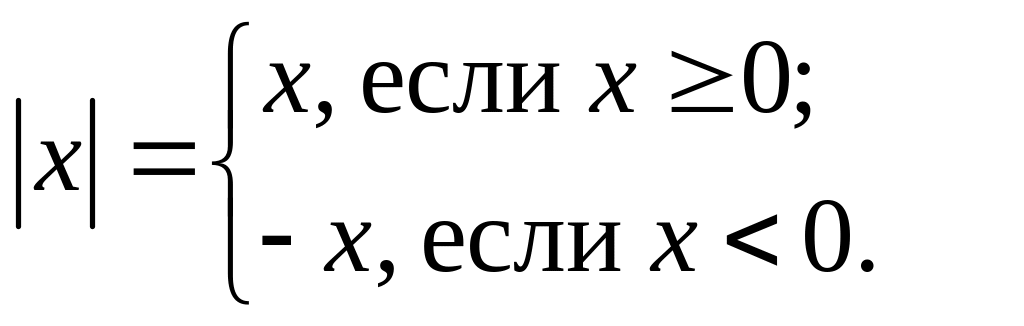 Обозначают:

Рассмотрим правила, по которым выполняют арифметические действия над числами множества .

Справедливость этих правил может быть доказана на основе свойства непрерывности множества с учетом того, что и арифметические операции в подчиняются указанным правилам. Операция вычитания сводится к операции сложения.

Определение 43. Разностью двух действительных чисел и называют действительное число вычисляемое по правилу: то есть разность двух действительных чисел и есть сумма числа и числа противоположного числу . Разность чисел и записывают в виде число − уменьшаемое, − вычитаемое. Операция деления сводится к операции умножения.

Определение 44. Частным от деления действительного числа на действительное число называют такое действительное число которое удовлетворяет равенству Частное чисел и записывают в виде или число − делимое, − делитель.

Таким образом, арифметические операции на возможны, за исключением деления на 0. При этом сумма, разность, произведение, частное двух положительных действительных чисел и является положительное действительное число. Значит, множество замкнуто относительно арифметических операций (исключая деление на ноль).

Множество чисел, замкнутое относительно арифметических операций, называют числовым полем. Итак, множество − числовое поле.

Законы и свойства арифметических операций на практически полностью совпадают с аналогичными законами и свойствами арифметических операций на множестве

3.9. Алгебраические и трансцендентные числа

Множество помимо деления на и может быть разделено на два других множества – множество алгебраических чисел и множество трансцендентных чисел.

Определение. Алгебраическим числом называют действительное число, являющееся корнем некоторого алгебраического уравнения вида с целыми коэффициентами, из которых хотя бы один отличен от нуля.

Определение. Трансцендентным числом называют действительное число, не являющееся корнем никакого алгебраического уравнения с целыми коэффициентами.

Множество включает множество алгебраических чисел, так как является корнем алгебраического уравнения первой степени . Отсюда также следует, что любое трансцендентное число иррационально. Множество всех алгебраических чисел образует счетное множество, а множество всех трансцендентных чисел – несчетное.

Вопросы для самопроверки

1. Обоснуйте необходимость расширения множества .

2. Что называют множеством положительных действительных чисел?

3. Сформулируйте определение положительного действительного числа.

4. В чем заключается аксиоматический метод построения научной теории? Какие требования предъявляют к системе аксиом?

5. Назовите неопределяемые понятия при аксиоматическом построении множества .

6. В чем заключается аксиоматическое построение множества ? Перечислите аксиомы данной системы.

7. Обоснуйте необходимость расширения множества .

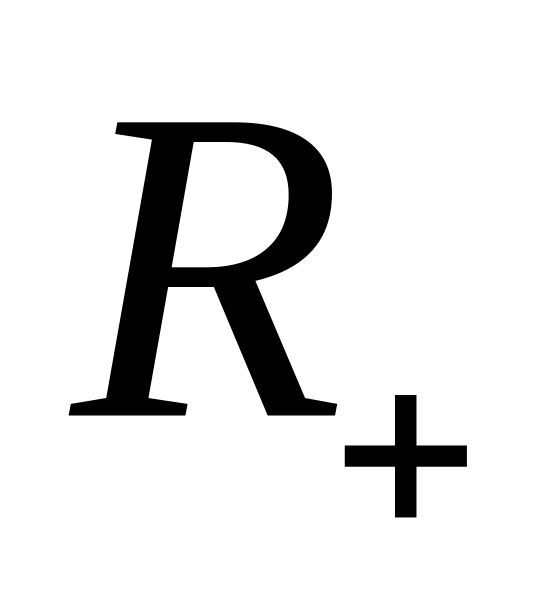8. Дайте определение отрицательного действительного числа.

9. Какие числа называют противоположными?

10. Дайте определение множества .

11. Как упорядочить множество ?

12. Дайте определение модулем (абсолютной величины) числа

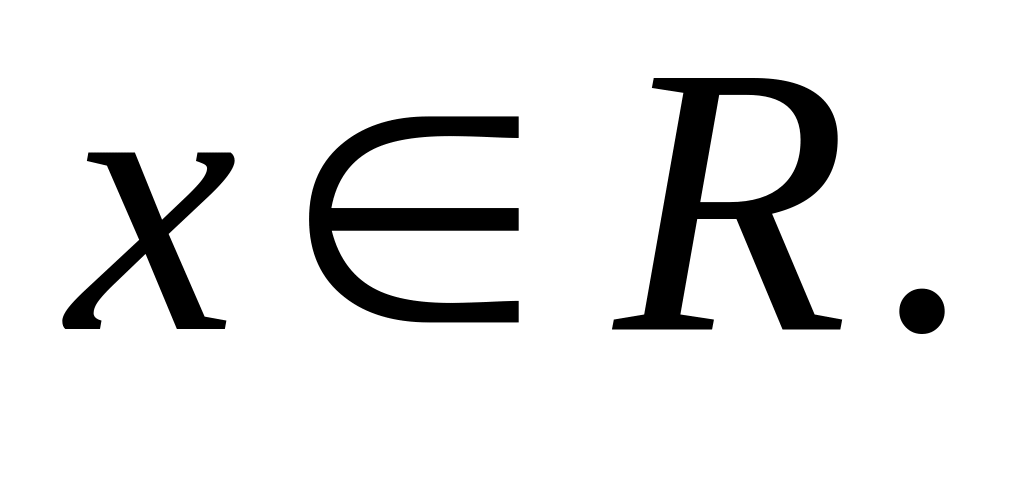
13. Сформулируйте правила, по которым выполняют арифметические действия над числами множества .

14. Сформулируйте определение алгебраического числа.

15. Сформулируйте определение трансцендентного числа.