3.4. Свойства множества

Теорема 55. Между любыми двумя различными положительных действительных чисел и заключено бесконечно много чисел множества то есть множество − плотно.

Доказательство. Пусть ,

По определению отношения «меньше» существует такой номер , что При и

Предположим, что минимальное число, при котором такое обязательно найдется, так как используем только приведенную запись действительных чисел. Число с определим следующим образом:

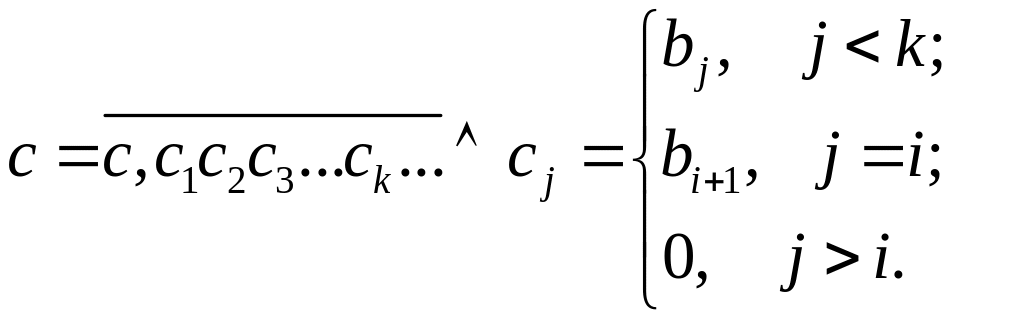
В этом случае, по определению «меньше»

Определение 33. Последовательностью вложенных отрезков называют последовательность отрезков для которой выполняется условие

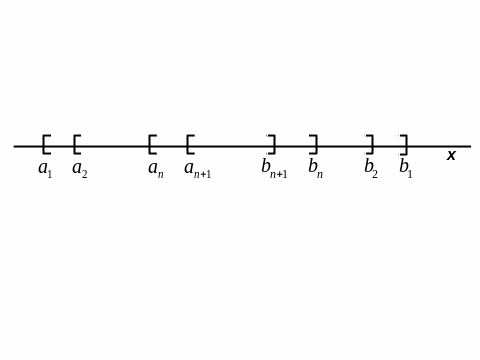
В указанной последовательности концы вложенных друг в друга отрезков, очевидно, удовлетворяют неравенствам: и располагаются на числовой оси следующим образом:

Теорема 56. Для всякой последовательности вложенных отрезков существует хотя бы одно число принадлежащее всем отрезкам этой последовательности.

Теоремы 56 и 57 выражают свойства множества называемое непрерывностью. Геометрически интерпретация этого свойства означает, что при изображении действительных чисел точками на прямой вся числовая ось заполнена ими без пробелов.

Теорема 57. Множество не является счетным.

Доказательство. Напомним определение счетности: счетным называют множество, которое эквивалентно множеству натуральных чисел.

Очевидно, что для доказательства теоремы достаточно показать, что какое-нибудь бесконечное собственное подмножество не является счетным.

Известно, что любое число из интервала (0;1) записывается в виде бесконечной десятичной дроби вида: где не все и никогда все цифры, начиная с некоторой, не могут равняться 9.

Обратно, всякая такая десятичная дробь дает одно из чисел интервала (0;1). Легко видеть, что интервал (0;1) есть бесконечное множество, т.к. одно содержит множество 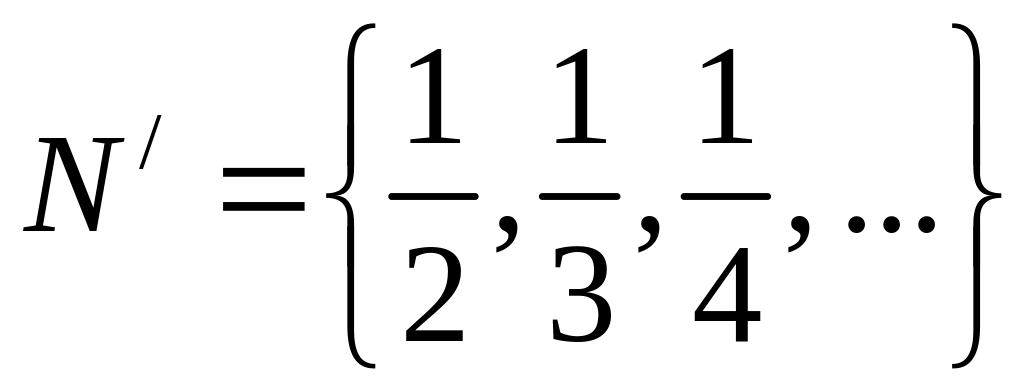равномощное множеству

Покажем, что (0;1) не является счетным множеством методом от противного. Тогда все числа интервала можно пронумеровать

При этом , , , …, .

Посмотрим теперь число следующим образом: берем цифру отличную от 0 и 9 берем цифру отличную от 0 или 9 0 9.

Дробь обладает нужными свойствами (она вовсе не имеет цифр 0 и 9). Значит, Но запись числа с отлична от записи всех чисел. Действительно, запись числа с отличается от так как от так как и т.д.

Не принадлежит множеству чисел Мы же предположили, что пронумерованы все числа интервала.

Теорема 58. Свойства множества . Множество бесконечное, плотное, линейно упорядоченное, несчетное, непрерывное, в нем нет, наименьшего и наибольшего числа.

Доказательство. Множество множество бесконечное, наибольший и наименьший элемент в нем отсутствуют. В теореме 55 доказано, что множество − плотное. Линейная упорядоченность множества следует из свойств отношений «меньше», «больше». Непрерывность множества следует из теорем 56 и 57. Из теоремы 57 следует, что множество

Теорема 59. Если последовательность вложенных отрезков с рациональными концами длины которых стремятся к нулю при то лежащее во всех отрезках этой последовательности.

Доказательство. Существование следует из теоремы 57. Докажем утверждение методом «от противного». Пусть и лежат во всех отрезках этой последовательности. Тогда справедливо

Если и приближенные значения и то можно показать, что при достаточно больших К следует так как длины отрезков последовательности при то для имеем но при , что невозможно. Полученное противоречие и доказывает утверждение.