Примеры и задачи на все действия с обыкновенными и десятичными дробями

Произведите указанные действия:

в)

Выполните арифметические операции:

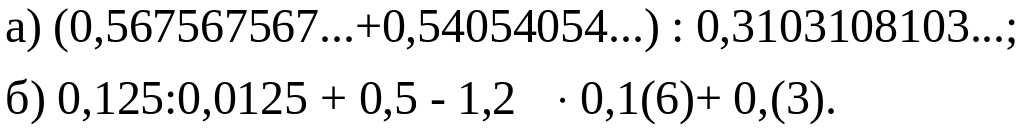
На основании зависимости между компонентами и результатом действий найти значение переменной :

Произведите указанные действия:

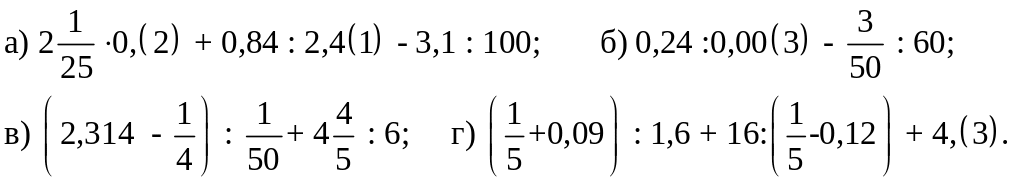
Выполните арифметические операции:

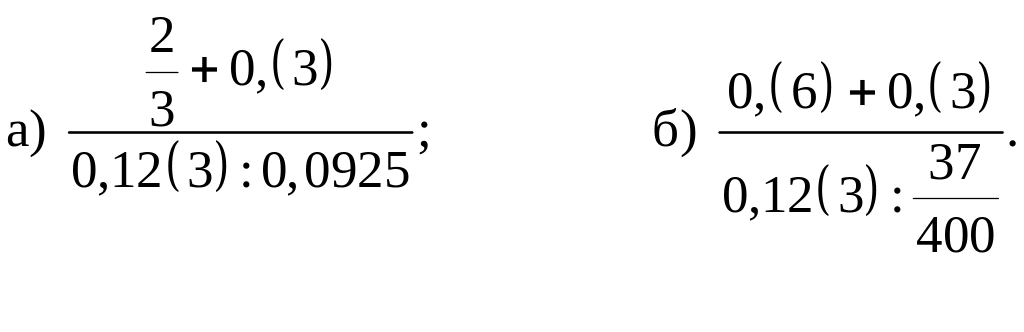
Выполните указанные действия:

Вычислите:

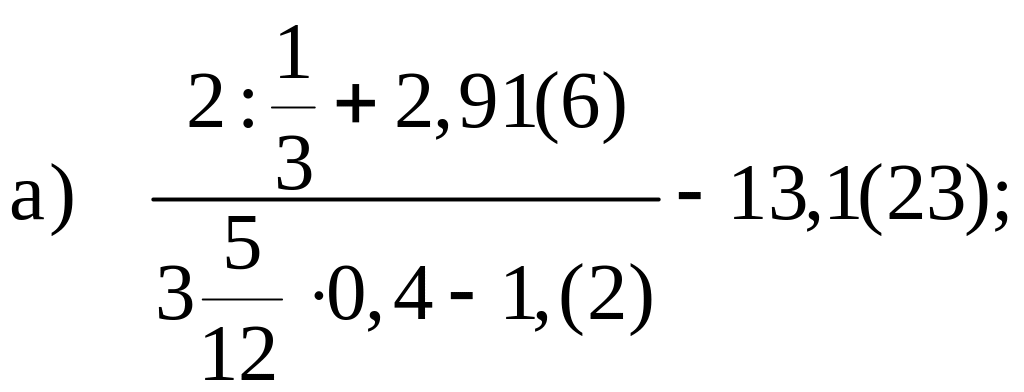
б)

в)

На основании зависимости между компонентами и результатом действий, найдите значение переменной х:

а)

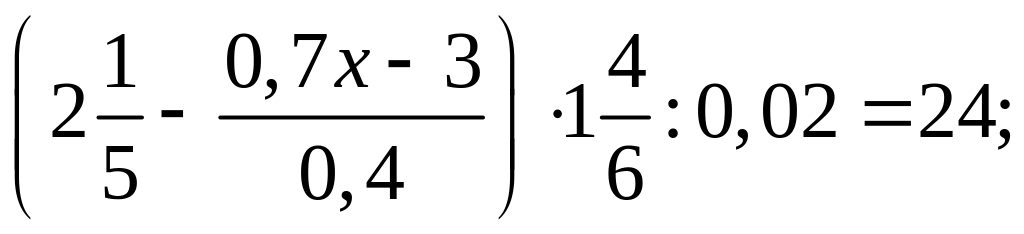
б)

в)

г)

д)

Понятие действительного числа

Определение 26. Множеством положительных действительных чисел называют объединение множества положительных рациональных чисел и множества положительных иррациональных чисел

Обозначают Таким образом,

Определение 28. Число, выражаемое конечной или положительной бесконечной десятичной дробью, называют положительным действительным числом.

Замечание. При записи действительных чисел в виде бесконечных десятичных дробей принято не использовать дроби с девяткой в периоде. Запись действительных чисел без использования 9 в периоде называется приведенной. Так, вместо 4,82(9) следует писать 4,83 или 4,83(0).

Для сравнения положительных действительных чисел и выполнения действий над ними бесконечные десятичные дроби заменяются конечными десятичными дробями. Для этого вспомним понятие приближенного значения действительного числа по избытку и по недостатку.

Определение 29. Приближенным значением числа по недостатку с точностью называется число приближенное значение числа по недостатку с точностью до есть конечная десятичная дробь которая получается из , если оставить целую часть числа и первые цифр после запятой, а все остальные цифры отбросить.

Определение 30. Приближенным значением числа по избытку с точностью называется число

Приближенное значение числа а по избытку с точностью до есть конечная десятичная дробь , которая получается из , если оставить целую часть числа и первые цифры после запятой, увеличить -ую цифру на единицу, а все остальные цифры отбросить.

Пример. Найти приближенное значение числа с точностью до 0,01.

Решение. Приближенное значение числа по недостатку с точностью : Приближенное значение числа по избытку с точностью :

3.3. Отношение порядка на множестве

Упорядочить множество можно задав на нем отношение «меньше».

Определение 31. Пусть даны два положительных действительных числа и . Число меньше числа , если выполнимо одно из следующих условий: и существует номер такой, что но

Замечание. В определении существенно то, что для чисел и используется приведенная запись, так как в противном случае 0,(9) 1, что неверно.

Определение 32.

Теорема 53. Для любых положительных действительных чисел и выполняется хотя бы одно из соотношений:

Теорема 54. Отношение «меньше» на множестве является отношением строгого порядка, то есть отношение «меньше» на множестве антирефлексивно, антисимметрично и транзитивно.

Итак, отношение «меньше» на является отношением строго порядка, а − линейно упорядоченным множеством.