Задачи на проценты

Напомним, что процентом называют одну сотую часть числа. Слово процент происходит от латинского pro centum, означающего от сотни или на сто.

Проценты были известны индусам ещё в V веке нашей эры. Это не удивительно, потому что в Индии с давних пор счёт вёлся в десятичной системе счисления. В Европе десятичные дроби появились на тысячу лет позже, их ввёл бельгийский учёный Симон Стевин. Он же в 1854 году впервые опубликовал таблицу процентов.

Один процент (пишут 1%) от некоторого числа есть 0,01 , 57% от числа а есть 0,57 и т. д. 100% от числа есть, очевидно, само число .

Чтобы выразить процент десятичной дробью или натуральным числом, нужно число, стоящее перед знаком %, разделить на 100.

Пример.

Для обратного перехода выполняется обратное действие.

Чтобы выразить число в процентах, надо это число умножить на 100.

Пример.

Пример. Найдем 173% от ?

Решение. 173 сотых части числа , то есть 1,73 .

Можно дать ответ и несколько иным образом. 173% от − это 100% от плюс еще 73% от ; но 100% от есть само число , а 73% от есть 0,73 . В итоге получаем: 173% от − это 1,73 .

Количество процентов может выражаться не только целыми, но и дробными числами.

Пример. 0,1% (ноль целых одна десятая процента) есть одна десятая часть от одной сотой части, то есть одна тысячная часть: 0,1% от равно 0,001 . Аналогично 43,8% от равно 43 сотых и 8 тысячных частей , то есть 0,438 ; 123,45% от равно 1,2345 и т.д.

Пример. Увеличим число на 62%?

Решение. К числу нужно прибавить 62% от него же самого. Получим новое число b: b= +0,62 =1,62 . Число b=1,62 есть результат увеличения числа на 62%. В таком случае говорят, что число b на 62% больше числа .

Аналогично уменьшить число на 14% означает, что из числа нужно вычесть 14% от него же самого. Получим число с: с= –0,14 =0,86 . Число с=0,86 есть результат уменьшения числа на 14%. В этом случае говорят, что число с на 14% меньше числа .

Частное двух этих чисел, выраженное в процентах, называется процентным отношением этих двух чисел.

Поскольку проценты выражаются дробями, то задачи на проценты являются по существу теми же задачами на дроби. Составные задачи на проценты решаются аналогично задачам на дроби. Для наглядности, как и раньше, можно использовать схему. Рассмотрим примеры.

Задача. Банк обещал своим клиентам годовой рост вклада 30%. Какую сумму денег может получить человек, вложивший в этот банк 450 тысяч рублей?

Решение.

1. – «прирост» за один год.

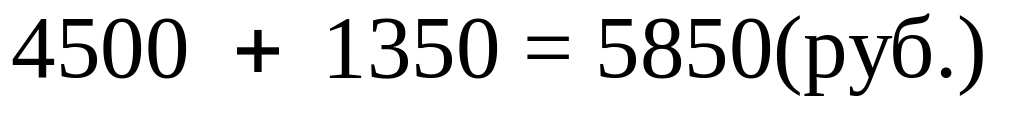2. будет находиться на счете в конце года.

Ответ. 5851 руб.

Задачу можно решить и иначе: сначала найти, сколько процентов составит сумма на счете в конце года от первоначальной: а затем вычислить 130% от 1500 руб.

Задача. Какую сумму следует положить в банк, выплачивающий 25% годовых, чтобы по истечении года получить 1000 руб.?

Решение.

1. составляет 1000 руб. от первоначального вклада.

2. сумма вклада.

Ответ. 800 руб.

Задача. В 200г. воды растворили 50г. соли. Какова концентрация полученного раствора?

Решение. Концентрацией раствора называют процент, который составляет масса вещества в растворе от массы раствора. Поэтому требуется вычислить процент, который составляет 50г. соли всей массы раствора.

1. масса полученного раствора.

2. 

Ответ. 20%.

Задача. В течение января цена на яблоки выросла на 30%, а в течение февраля – на 20%. На сколько процентов поднялась цена за 2 месяца?

Решение. Утверждать, что цена выросла на 50%, нельзя, поскольку «первые» 30% подсчитываются от цены в конце декабря, а «вторые» 20% ‒ от другой величины, цены на конец января.

Потом будем рассуждать последовательно, обозначив для удобства первоначальную цену S. В конце января она стала равна 1,3S. В конце февраля – . Следовательно, она выросла на 56%.

Решение можно записать следующим образом.

Пусть S – первоначальная цена.

1) 1,3S – цена в конце января (130% от S).

2) – цена в конце февраля (120% от 1,3S).

3)1,56S составляет 156% от S.

Ответ. За 2 месяца цена выросла на 56%.

Если человек не вносит своевременную плату за квартиру, то на него налагается штраф, который называется «пеня». Так в Москве пеня составляет 1% от суммы квартплаты за каждый день просрочки. Поэтому, например, за 19 дней просрочки, сумма составит 19% от суммы квартплаты, и в месте, скажем, со 100 руб. квартплаты человек должен будет внести пеню .

Выведем общую формулу. Пусть S – ежемесячная оплата, пеня составляет p% оплаты за каждый день просрочки, а n – число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.

Тогда за n дней просрочки, пеня составит pn% от S, или , а всего придётся заплатить . Таким образом, .

Данная формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Задача. Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 рублей. Какая сумма будет на его счёте через полгода?

Решение. Для решения задачи достаточно подставить в формулу величину процентной ставки p=2, числа месяцев n=6 и первоначального вклада S=500: будет через полгода на вкладе.

Ответ. 560 руб.

В Сберегательном банке России для некоторых видов вкладов принята следующая система начисления денег. За первый год нахождения внесенной суммы на счете начисляется а% от нее. В конце года вкладчик может снять со счета эти деньги – «проценты», как их обычно называют. Если же он этого не сделал, то они присоединяются к начальному вкладу, и поэтому в конце следующего года а% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

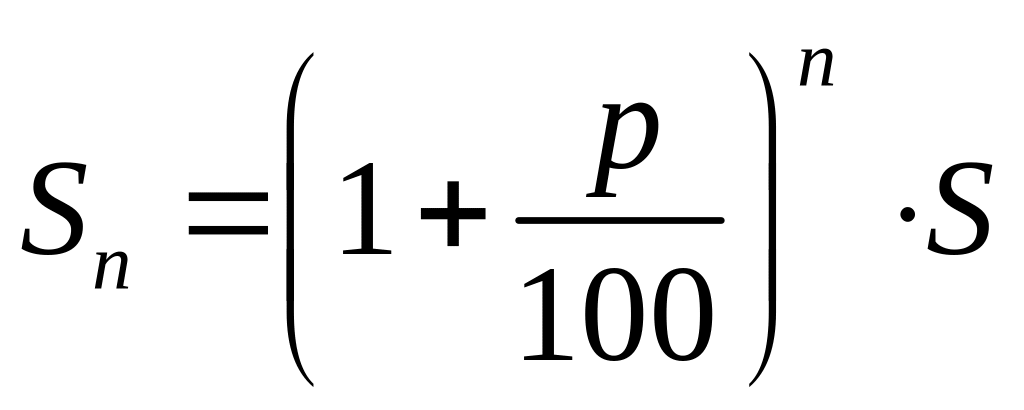
Данную формулу называют формулой сложного процентного роста, или формулой сложных процентов.

Задача. Какая сумма будет на срочном счёте вкладчика через 4 года, если банк начисляет 10% годовых и внесённая сумма равна 2 000 рублей?

Решение. Подставим в формулу значения процентной ставки p=10, количество лет n=4 и величину первоначального вклада S=2000, получим: будет через 4 года на данном счёте.

Ответ. 2928,2 рубля.