
- •Предисловие
- •Содержание
- •Глава1……………………………………………………………….
- •Глава 2
- •Глава 3. Действительные числа
- •Введение
- •Глава 1.
- •1.1. Расширение понятия числа
- •1.2. История возникновения и развития понятия «рационального числа»
- •1.3. Понятие дроби
- •1.4. Отношение равенства дробей Определение 6. Две дроби и называют равными, если
- •1.5. Приведение дробей к общему знаменателю
- •1.6. Действия с дробями
- •Вопросы для самопроверки
- •Задания для самопроверки
- •Глава 2. Множество положительных рациональных чисел
- •2.1. Понятие положительного рационального числа
- •Вопросы для самопроверки
- •2.2. Отношения на множестве
- •2.2.1. Отношение равенства
- •2.2.2. Отношение «меньше»
- •2.2.3. Свойства отношения «меньше»
- •2.2.4. Отношение больше на множестве
- •Вопросы для самопроверки
- •2.5. Операции на множестве
- •2.5.1. Операция сложения на
- •2.6. Свойства операции сложения на
- •Вопросы для самопроверки
- •2.6.2. Вычитание на
- •2.8. Свойства операции вычитания
- •Вопросы для самопроверки
- •2.6.3. Умножение положительных рациональных чисел
- •2.10. Свойства операции умножения
- •Вопросы для самопроверки
- •2.11. Деление положительных рациональных чисел
- •2.11. Свойства операции деления
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Решение арифметических задач с дробями
- •Задачи на отыскание дроби от заданного числа
- •Задачи на отыскание числа по заданной величине, по дроби
- •Задачи на отыскание дроби от заданного числа и числа по заданной величине
- •Задачи на совместную работу
- •Задачи на движение
- •2.12. Десятичные дроби
- •2.13. Операции над десятичными дробями
- •2.14. Преобразование обыкновенных дробей в десятичные
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Задачи на проценты
- •Задания для самостоятельного решения
- •Глава 3. Действительные числа
- •3.1. Бесконечные дроби
- •3.2. Понятие иррационального числа
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Примеры и задачи на все действия с обыкновенными и десятичными дробями
- •Понятие действительного числа
- •3.3. Отношение порядка на множестве
- •3.4. Свойства множества
- •3.5. Арифметические операции на
- •Вопросы для самопроверки
- •3.6. Аксиоматическое построение множества
- •3.7. Множество
- •3.8. Арифметические операции на множестве
- •3.9. Алгебраические и трансцендентные числа
- •Вопросы для самопроверки
- •3.10. Приближенные вычисления
- •3.11. Округление чисел
- •Вопросы для самопроверки
- •Литература
Задачи на отыскание дроби от заданного числа
Сколько частей составляет:
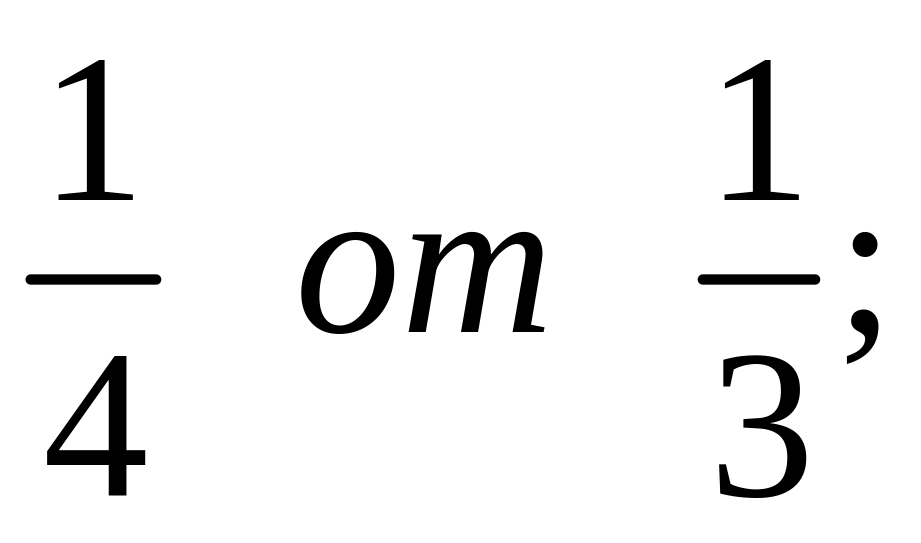
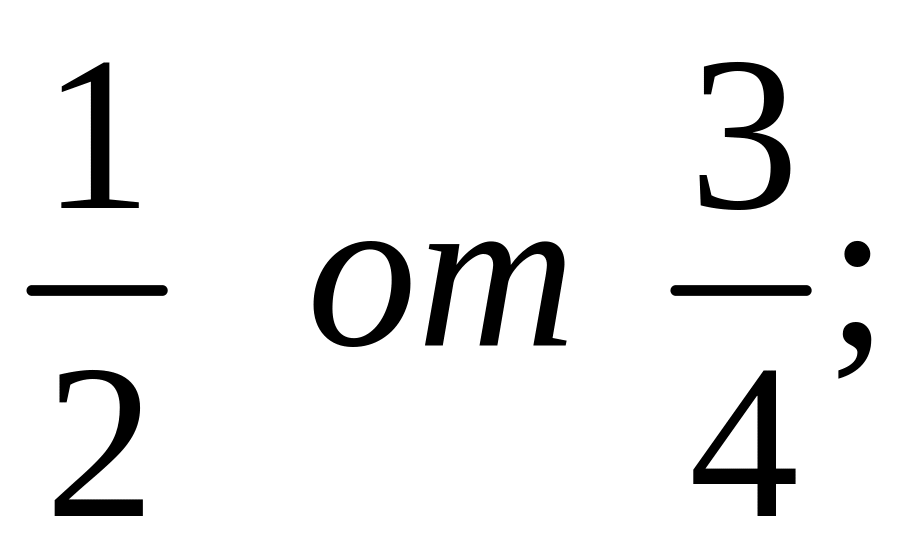
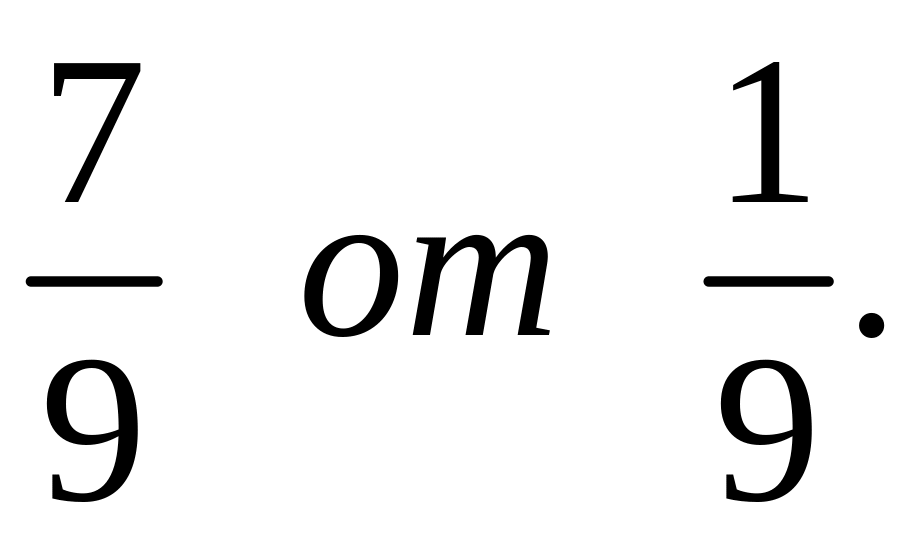
Произведение двух чисел
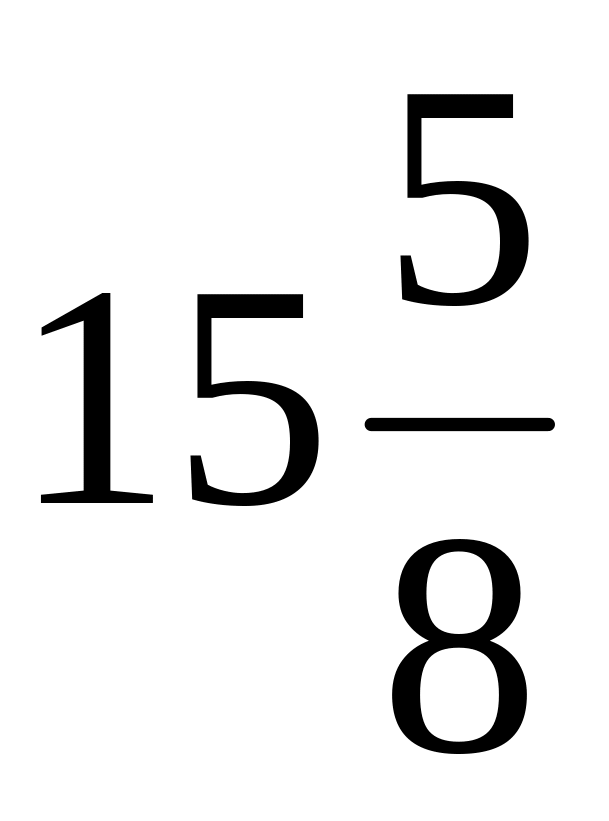 ;
одно из них 15. Найдите другое число.
;
одно из них 15. Найдите другое число.Что больше: а) или
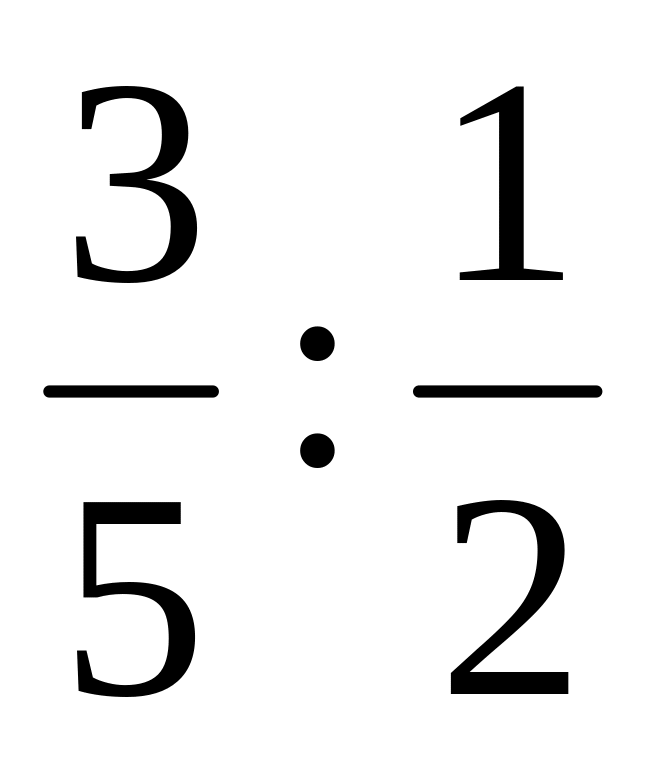 ; б)
; б)
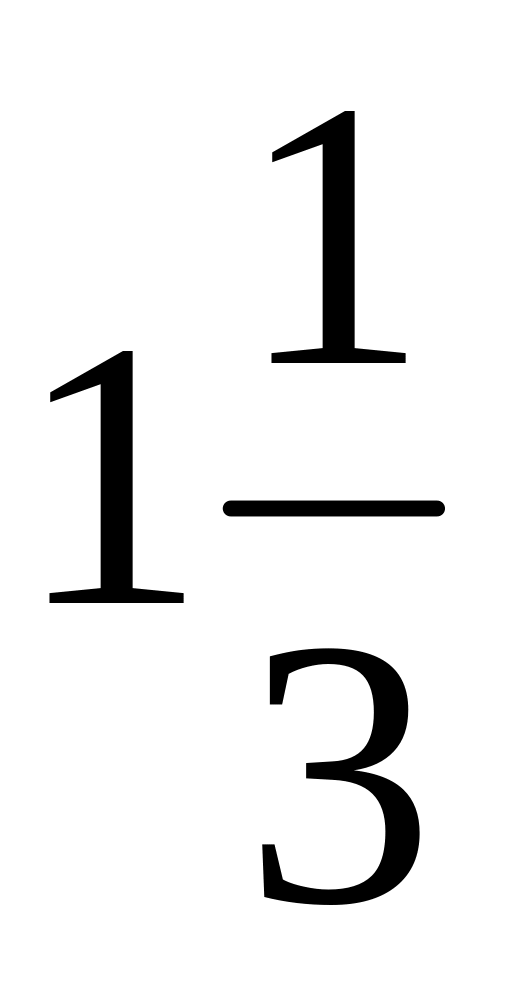 или
или
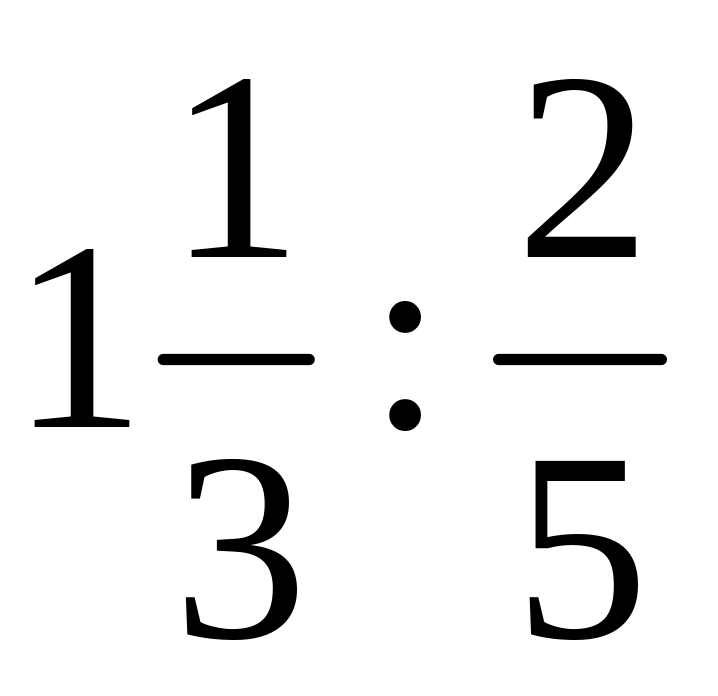 ?
?Найдите число,
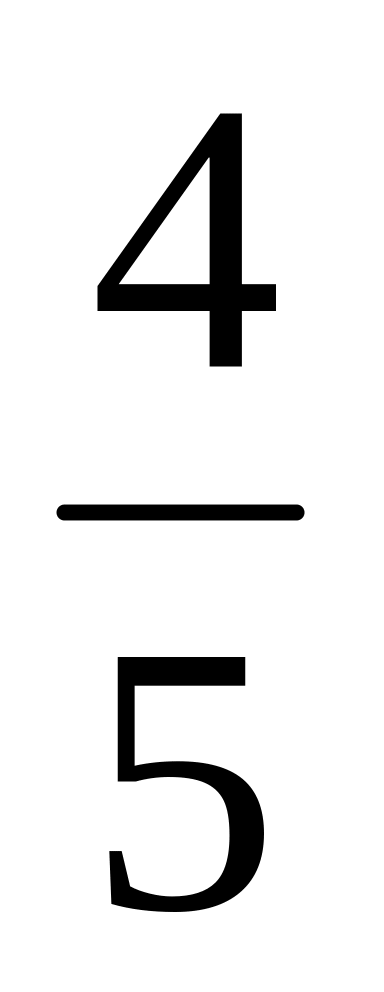 которого равно
которого равно
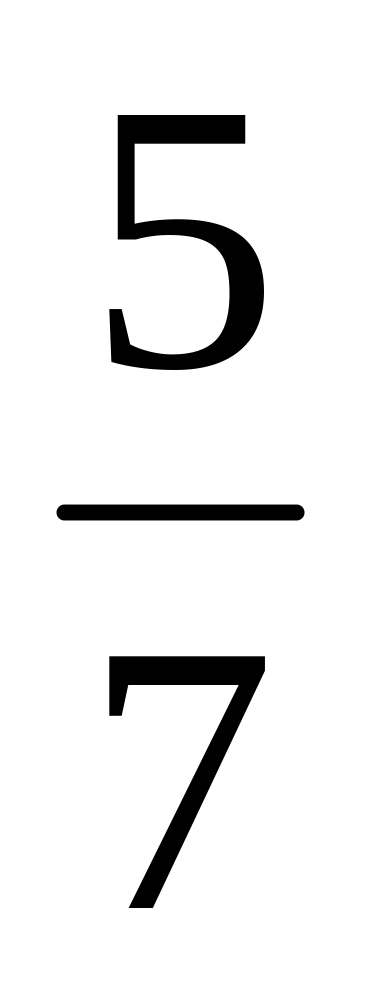 от 350.
от 350.Найдите числа 60.
Увеличь число 12 на этого числа.
Уменьшите 7 на этого числа.
Найдите: а)
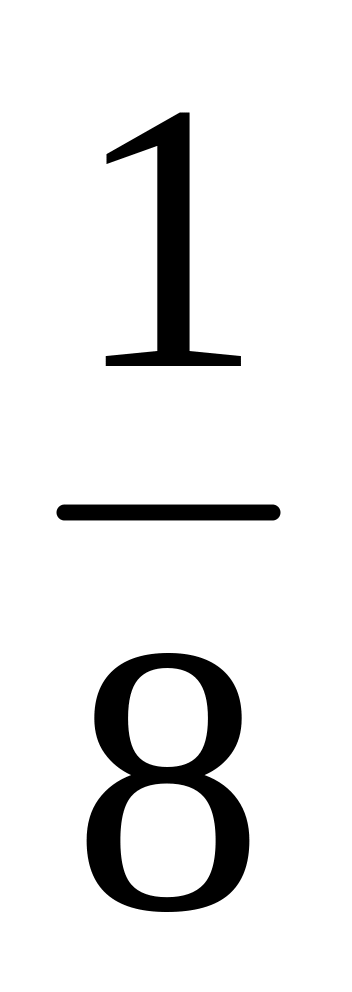 ; б)
;
в)
; б)
;
в)
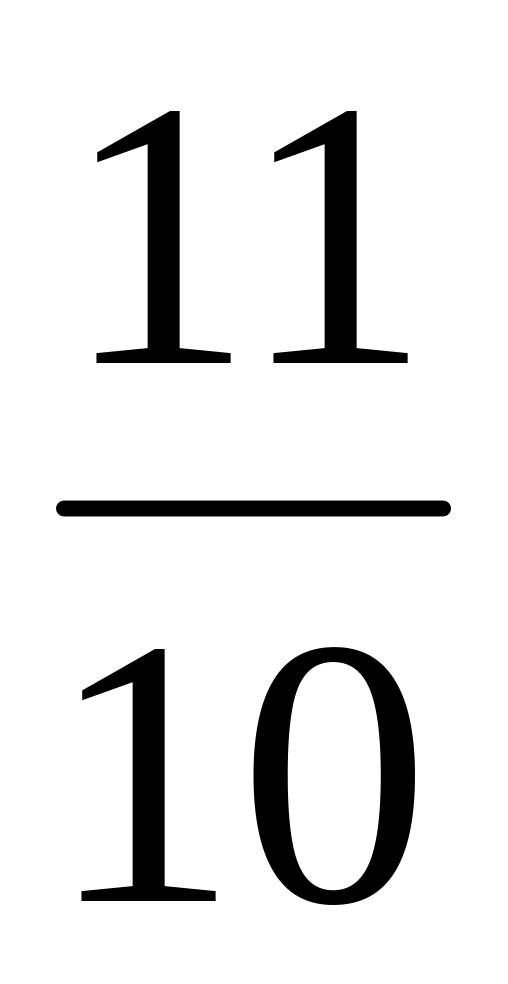 ; г)
1
от числа
; г)
1
от числа
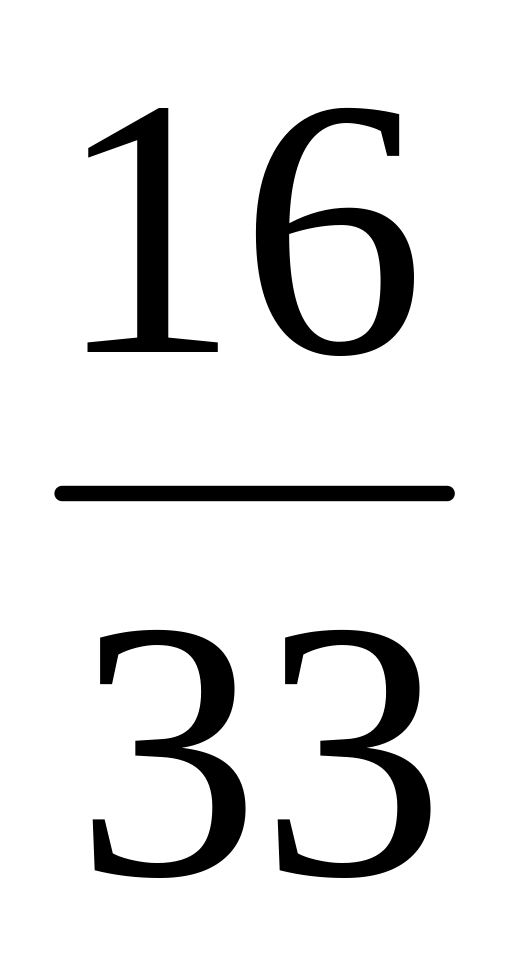 .
.Что больше от 60 или
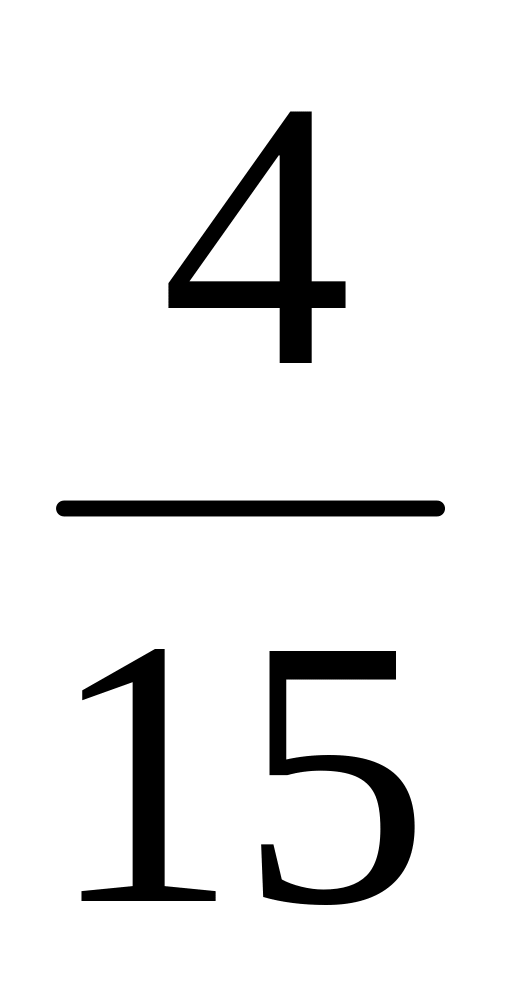 от 60?
от 60?от 60 или от 600?
от 60 или от 135?
Решите задачи.
При размоле пшеницы получается: муки от всего количества; манной крупы –
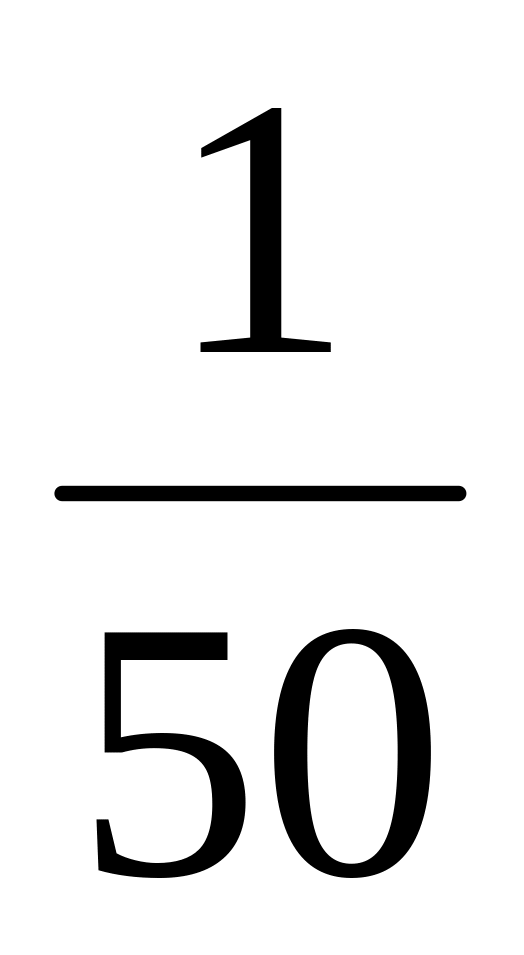 ;
а остальную часть составляют отруби.
Сколько муки, манки и отрубей можно
получить из 3 тонн пшеницы.
;
а остальную часть составляют отруби.
Сколько муки, манки и отрубей можно
получить из 3 тонн пшеницы.Мать оставила для четырех своих сыновей тарелку слив, а сама ушла на работу. Первым пришел из школы младший сын. Увидев на тарелке сливы, он съел третью часть и ушел гулять. Вторым пришел средний сын. Думая, что его братья не ели слив, он съел третью часть того, что было на тарелке, и тоже ушел гулять. Позднее всех пришел старший сын и съел 4 сливы – третью часть слив, которые он увидел на тарелке. Сколько слив было вначале?
Собрано в течение 4 дней 602 кг разных семян. В первый день собрано
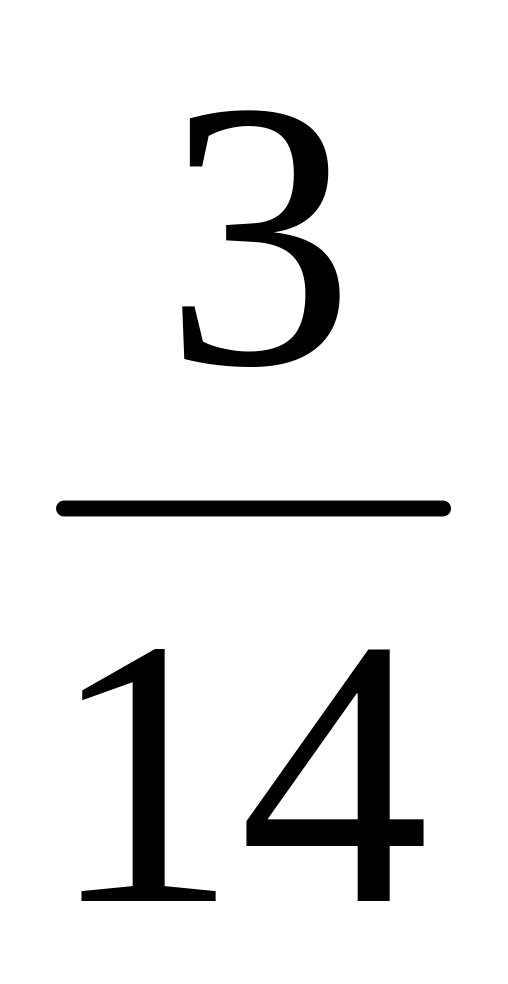 всего количества, во второй – в 1
раза
больше, чем в первый, в третий день –
того, что собрали в первые два дня
вместе, и в четвертый день – остальные
семена. Сколько семян собрано в четвертый
день?
всего количества, во второй – в 1
раза
больше, чем в первый, в третий день –
того, что собрали в первые два дня
вместе, и в четвертый день – остальные
семена. Сколько семян собрано в четвертый
день?Число юношей школы составляет числа девушек этой школы. Какую часть всех учащихся составляют юноши? Сколько девушек в школе, если общее число 420 человек?
В пачке 250 листов бумаги. На перепечатывание одной рукописи ушло пачки, на перепечатывание другой рукописи – остатка. Сколько осталось чистых листов?
Задачи на отыскание числа по заданной величине, по дроби
Найдите число, которого равны 40.
Найдите число,
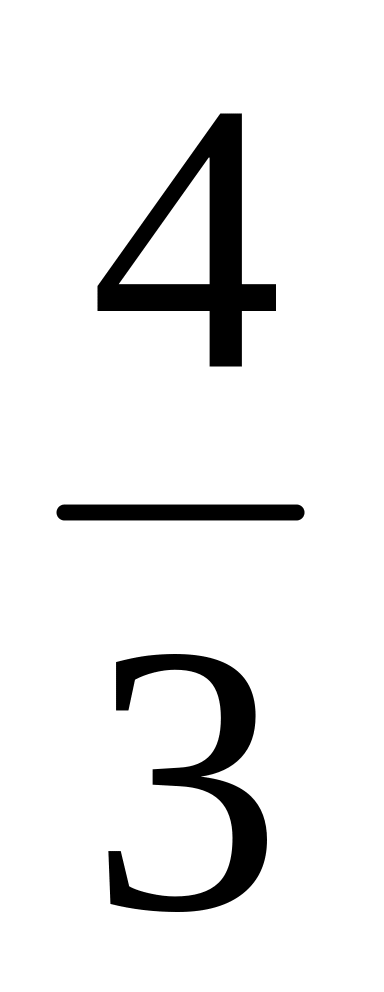 которого равны: а) 4; б)
;
в) 28; г) 4
?
которого равны: а) 4; б)
;
в) 28; г) 4
?Найдите число, для которого 100 составляет: а) ; б) ; в) 1 ; г) 2 ?
На настилку площади пола израсходовали 15 досок. Сколько таких досок требуется для настилки всего пола?
В первый день продано имеющейся ткани, во второй день того, что продано в первый, а в третий всю оставшуюся ткань. Сколько метров ткани продано, если в третий день продано на 192 метра больше, чем во второй?
Решите задачи.
Расстояние между двумя городами мотоциклист проехал за 3 часа. В первый час он проехал
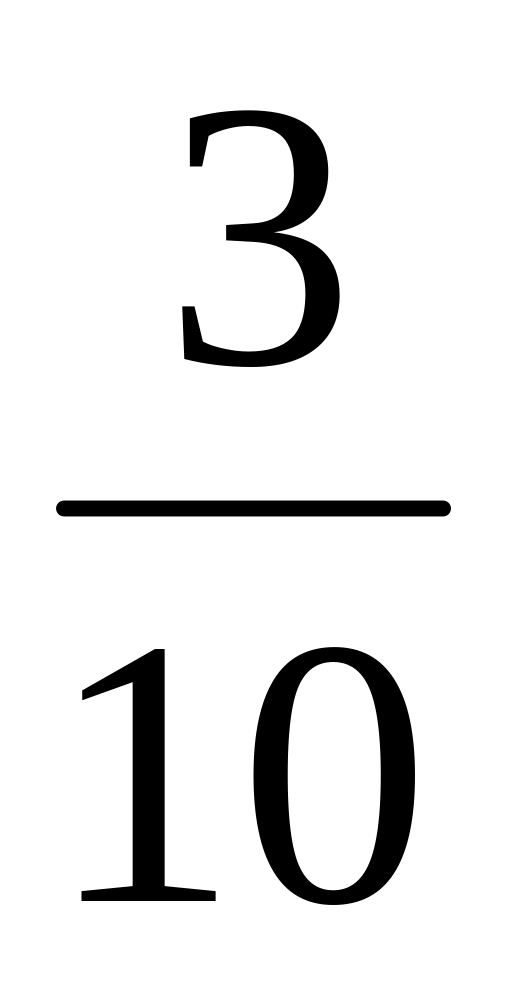 всего пути, во второй час –
всего пути, во второй час –
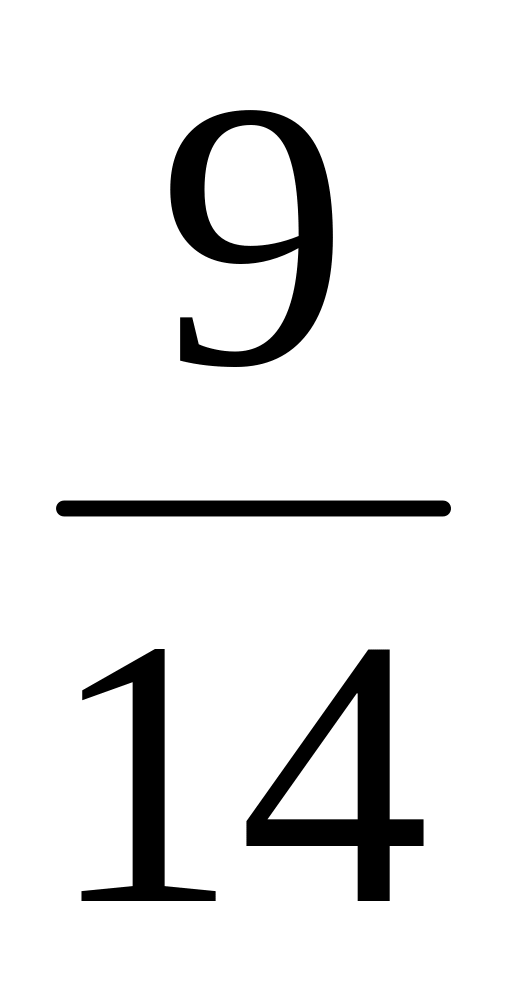 остатка; в третий час – остальное
расстояние. Известно, что в третий час
мотоциклист проехал на 12
км меньше, чем во второй час. Каково
расстояние между городами и сколько
километров проехал мотоциклист в первый
час?
остатка; в третий час – остальное
расстояние. Известно, что в третий час
мотоциклист проехал на 12
км меньше, чем во второй час. Каково
расстояние между городами и сколько
километров проехал мотоциклист в первый
час?Выход масла из сливок составляет веса молока. Сколько требуется молока, чтобы получить 1 ц масла?
Фирма израсходовала в первую неделю имеющегося у нее запаса сырья, во вторую неделю – остатка. Сколько сырья осталось, если в первую неделю расход сырья был на тонны больше, чем во вторую?
Два мальчика собрали 96 грибов. Известно, что числа грибов, собранных первым мальчиком, численно равны числа грибов, собранных вторым мальчиком. Сколько грибов собрали оба мальчика?
Найти число, если от него равны числу, которого составляют 25.
В трех районах города проживает 12000 человек. Сколько человек живет в каждом районе, если известно, что числа жителей первого района равны числа жителей второго района и числа жителей третьего района.
В фирме работает 99 человек. Сколько из них мужчин и женщин, если числа всех мужчин равна числа всех женщин?
