
- •Предисловие
- •Содержание
- •Глава1……………………………………………………………….
- •Глава 2
- •Глава 3. Действительные числа
- •Введение
- •Глава 1.
- •1.1. Расширение понятия числа
- •1.2. История возникновения и развития понятия «рационального числа»
- •1.3. Понятие дроби
- •1.4. Отношение равенства дробей Определение 6. Две дроби и называют равными, если
- •1.5. Приведение дробей к общему знаменателю
- •1.6. Действия с дробями
- •Вопросы для самопроверки
- •Задания для самопроверки
- •Глава 2. Множество положительных рациональных чисел
- •2.1. Понятие положительного рационального числа
- •Вопросы для самопроверки
- •2.2. Отношения на множестве
- •2.2.1. Отношение равенства
- •2.2.2. Отношение «меньше»
- •2.2.3. Свойства отношения «меньше»
- •2.2.4. Отношение больше на множестве
- •Вопросы для самопроверки
- •2.5. Операции на множестве
- •2.5.1. Операция сложения на
- •2.6. Свойства операции сложения на
- •Вопросы для самопроверки
- •2.6.2. Вычитание на
- •2.8. Свойства операции вычитания
- •Вопросы для самопроверки
- •2.6.3. Умножение положительных рациональных чисел
- •2.10. Свойства операции умножения
- •Вопросы для самопроверки
- •2.11. Деление положительных рациональных чисел
- •2.11. Свойства операции деления
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Решение арифметических задач с дробями
- •Задачи на отыскание дроби от заданного числа
- •Задачи на отыскание числа по заданной величине, по дроби
- •Задачи на отыскание дроби от заданного числа и числа по заданной величине
- •Задачи на совместную работу
- •Задачи на движение
- •2.12. Десятичные дроби
- •2.13. Операции над десятичными дробями
- •2.14. Преобразование обыкновенных дробей в десятичные
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Задачи на проценты
- •Задания для самостоятельного решения
- •Глава 3. Действительные числа
- •3.1. Бесконечные дроби
- •3.2. Понятие иррационального числа
- •Вопросы для самопроверки
- •Задания для самостоятельного решения
- •Примеры и задачи на все действия с обыкновенными и десятичными дробями
- •Понятие действительного числа
- •3.3. Отношение порядка на множестве
- •3.4. Свойства множества
- •3.5. Арифметические операции на
- •Вопросы для самопроверки
- •3.6. Аксиоматическое построение множества
- •3.7. Множество
- •3.8. Арифметические операции на множестве
- •3.9. Алгебраические и трансцендентные числа
- •Вопросы для самопроверки
- •3.10. Приближенные вычисления
- •3.11. Округление чисел
- •Вопросы для самопроверки
- •Литература
Вопросы для самопроверки
Дайте определение частного положительных рациональных чисел.
Сформулируйте необходимое условие существования частного положительных рациональных чисел.
Докажите, что частное от деления положительных рациональных чисел от выбора представителей этих чисел не зависит
Сформулируйте определение частичной алгебраической бинарной операции деления положительных рациональных чисел.
Укажите свойства операции деления положительных рациональных чисел.
Сформулируйте теорему о связи операции деления с умножением.
Докажите, что
Укажите свойства множества .
Сформулируйте теорему Архимеда.
Задания для самостоятельного решения
Дайте определение рационального числа. Приведите примеры рациональных чисел. Что является представителем рационального числа? Что вы можете сказать о несократимом представителе рационального числа.
Найдите истинностные значения данных высказываний: а) дробь
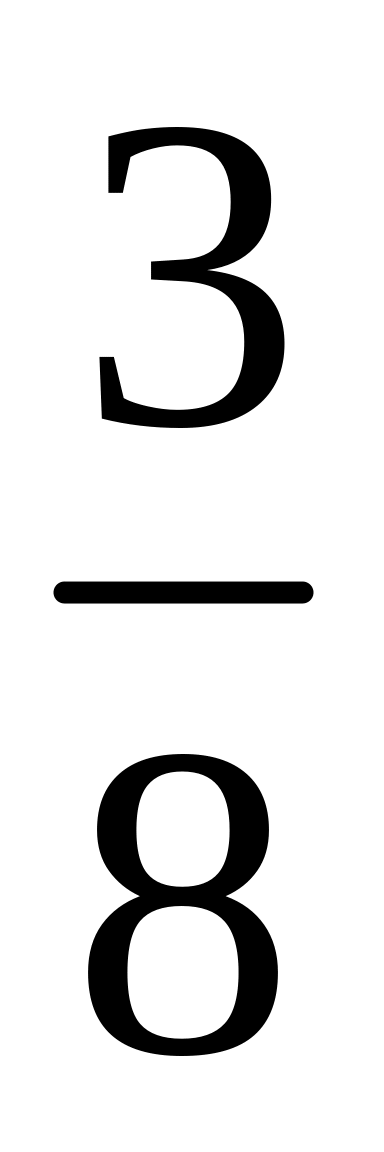 является представителем некоторого
рационального числа; б)
является представителем некоторого
рационального числа; б)
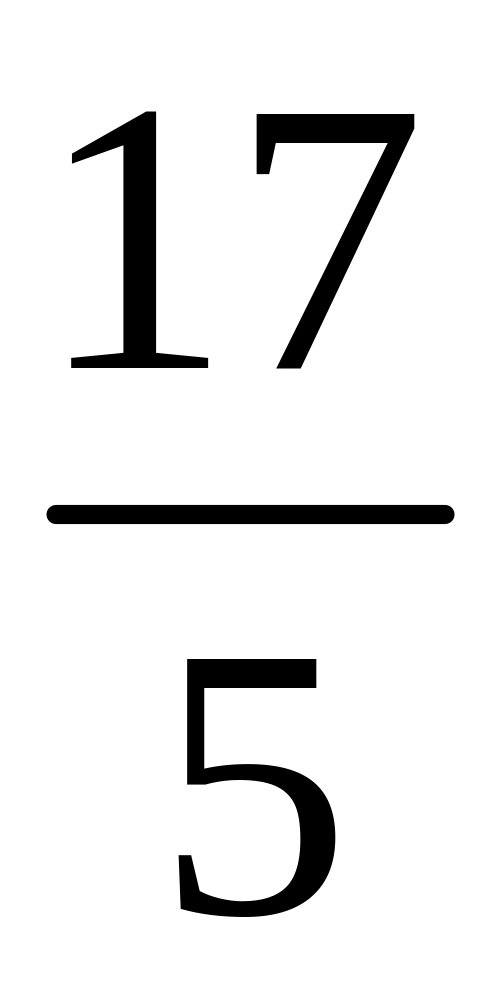 ‒ дробь; в)
‒ положительное рациональное число.
‒ дробь; в)
‒ положительное рациональное число.
Что называют суммой положительных рациональных чисел и ? Дайте определение операции сложения положительных рациональных чисел. Сложите рациональные числа:
1)
![]() +
+![]() ; 2)
+
; 3)
+
; 4)
; 2)
+
; 3)
+
; 4)
![]() +
+![]() ;
;
5)
![]() +
+![]() ; 6)
; 6)
![]() +
+![]() ; 7)
; 7)
![]() +
+![]() ; 8)
; 8)
![]() +
+![]() ;
;
9)
+
+
; 10)
+![]() +
11)
+
11)
![]() +
+![]() +
; 12)
+
+
+
; 12)
+
+![]() ;
;
13)
![]() ; 14)
; 14)
![]()
15)
![]() ; 16)
; 16)
![]() ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]() .
.
Сформулируйте свойства бинарной алгебраической операции сложения положительных рациональных чисел. Выполните сложение рациональных чисел, использовав свойства операции сложения:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
Выполните вычитание дробей:
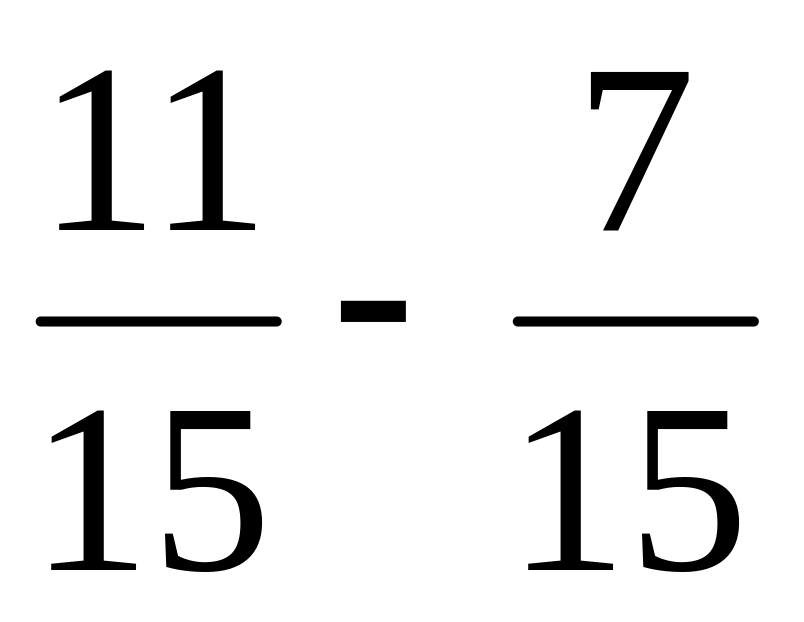 ;
;
 ;
;
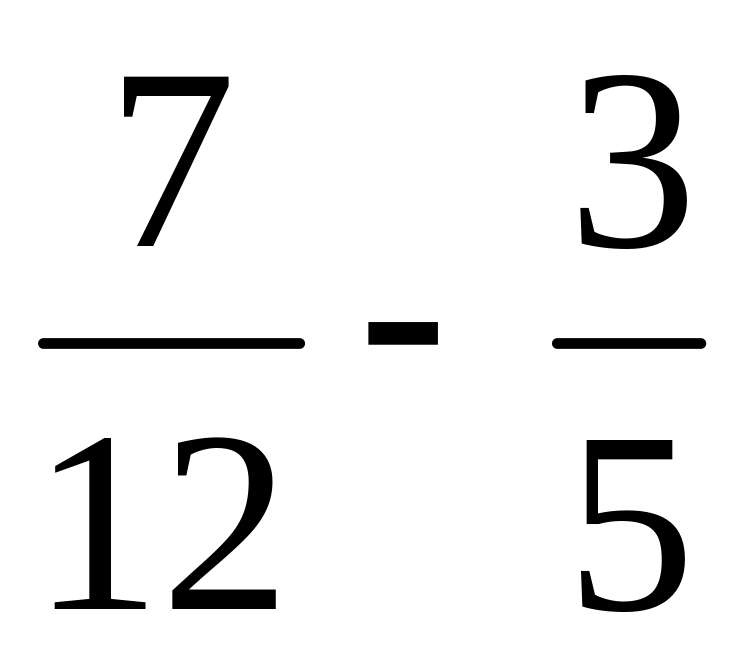 ;
;
 .
.Дайте определение разности положительных рациональных чисел и . Что называют операцией вычитания положительных рациональных чисел? Выполните вычитание рациональных чисел:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() 9)
9)
![]() ;
;
10)
![]() .
.
Вспомните теорему о связи операции сложения положительных рациональных чисел и вычитания положительных рациональных чисел. Выполните вычитание рациональных чисел и выполните проверку сложением:
 .
.На сколько необходимо уменьшить число
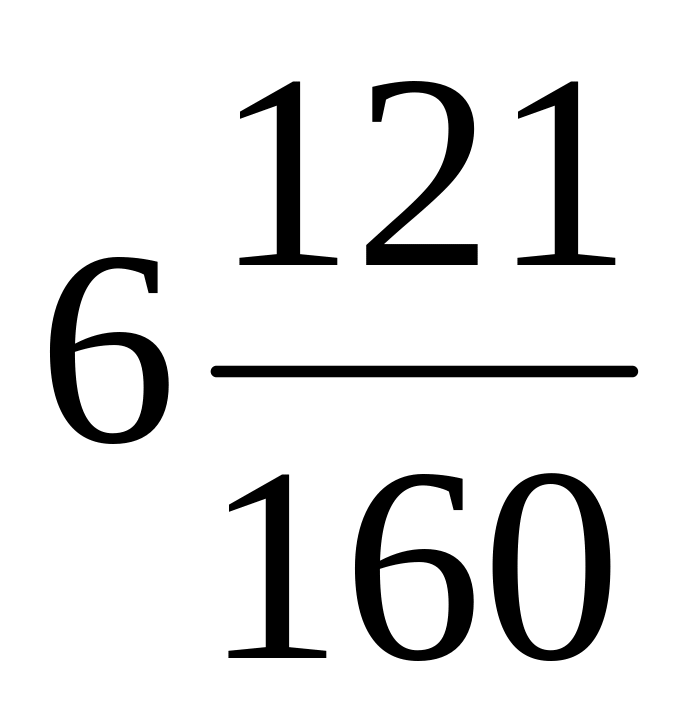 ,
чтобы получить
,
чтобы получить
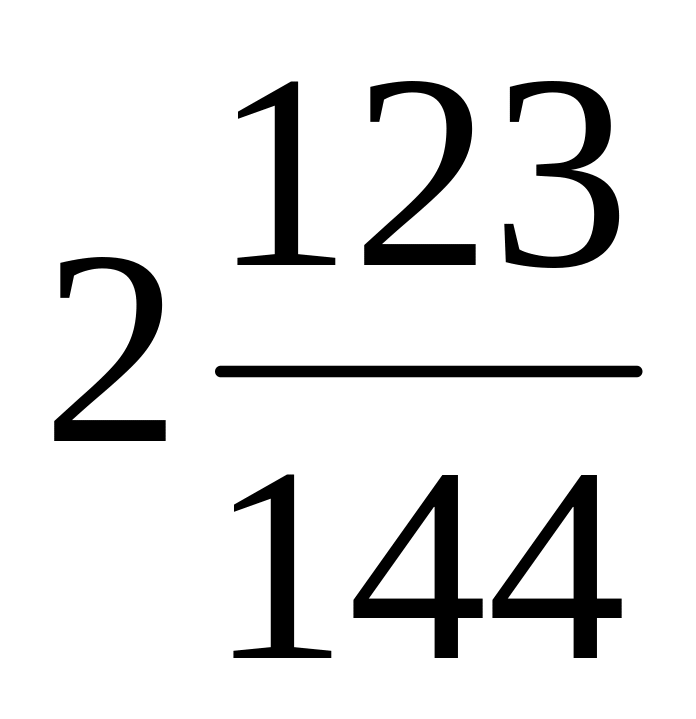 ?
?Найдите число, которое на
 меньше
меньше
 .
.Докажите, что если
 натуральные числа и
натуральные числа и
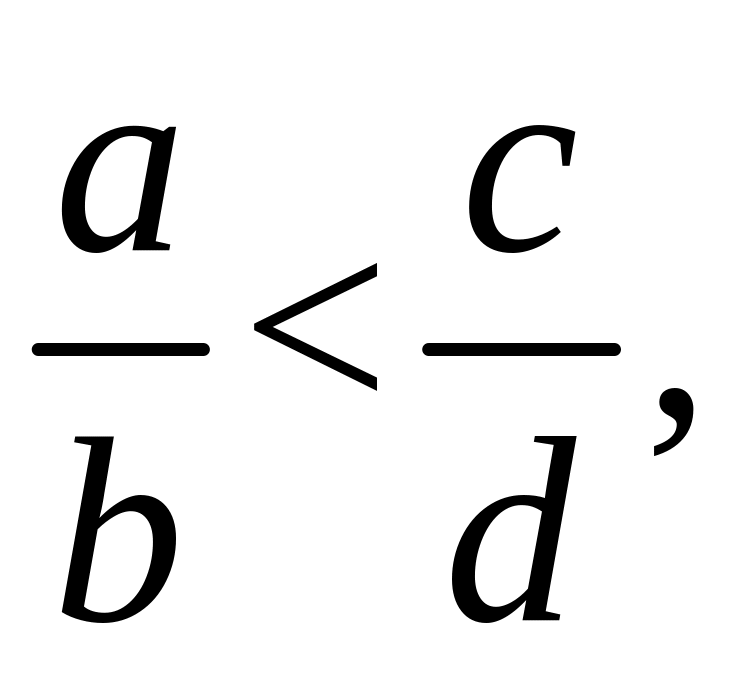 то
то

Сформулируйте свойства частичной бинарной алгебраической операции вычитания положительных рациональных чисел. Выполните вычитание рациональных чисел:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() .
.
На основании зависимости между компонентами и результатом действия найдите значение переменной
 :
:
а)
 б)
б)
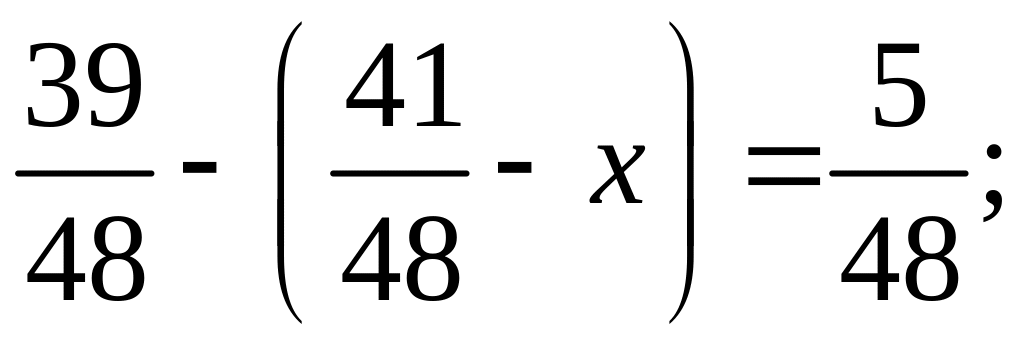
в)
 г)
г)
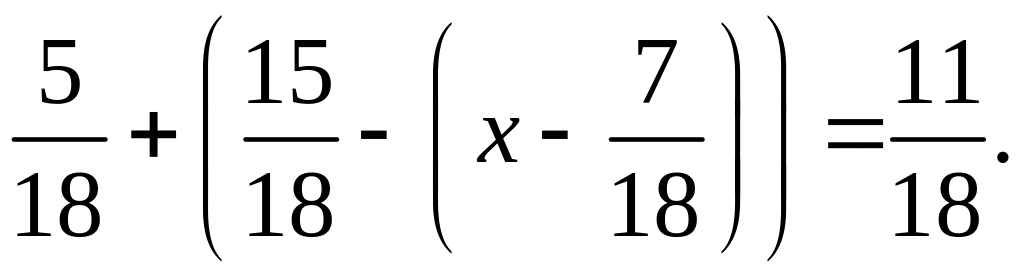
Дайте определение произведения положительных рациональных чисел. Найдите произведение рациональных чисел:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ; ж)
; ж)
![]() ; з)
; з)
![]() .
.
Дайте определение бинарной алгебраической операции умножения положительных рациональных чисел. Выполните умножение: а)
 ; б)
; б)
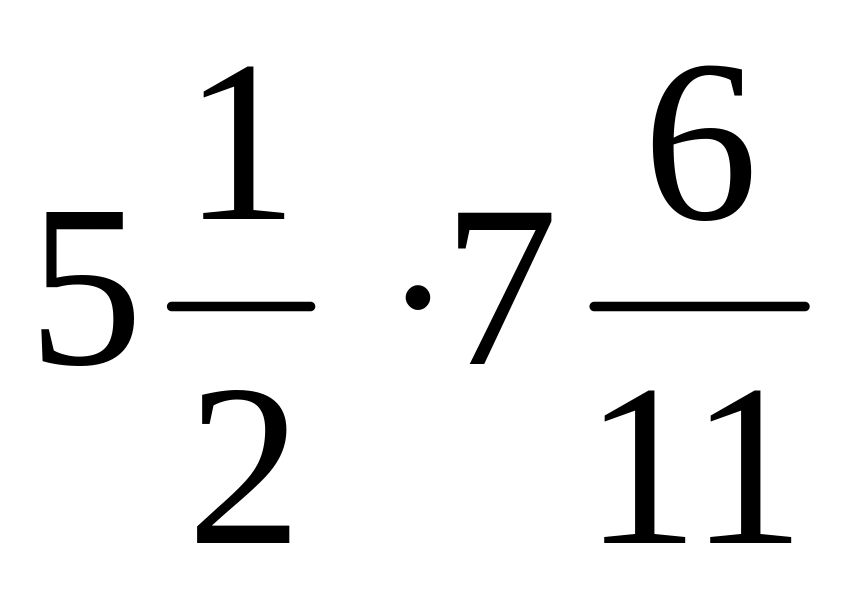 ; в)
; в)
 ; г)
; г)
 ; д)
; д)
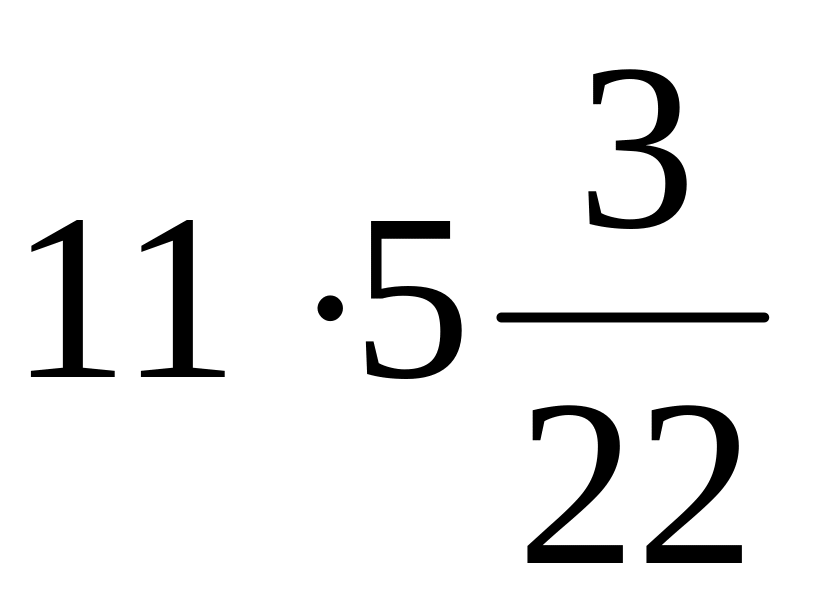 .
.Сформулируйте свойства операции умножения на Q+. Выполните умножение удобным способом:
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Выполните действия с положительными рациональными числами: а)
 ; б)
; б)
 .
.Выполните умножение рациональных чисел:
а)
![]() ; б)
; в)
.
; б)
; в)
.
Выполните указанные действия на Q+:
а)
; б)
![]() .
.
Выполните деление дробей: а)
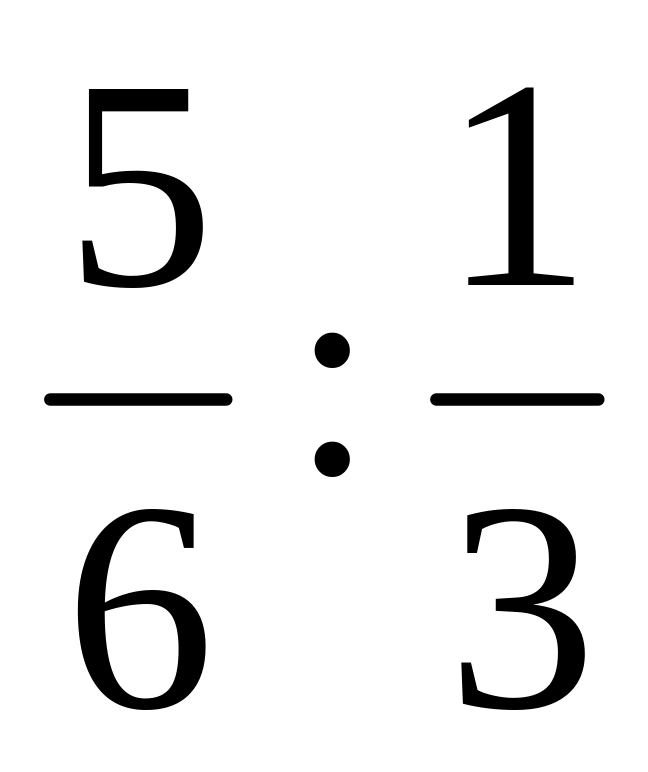 ; б)
; б)
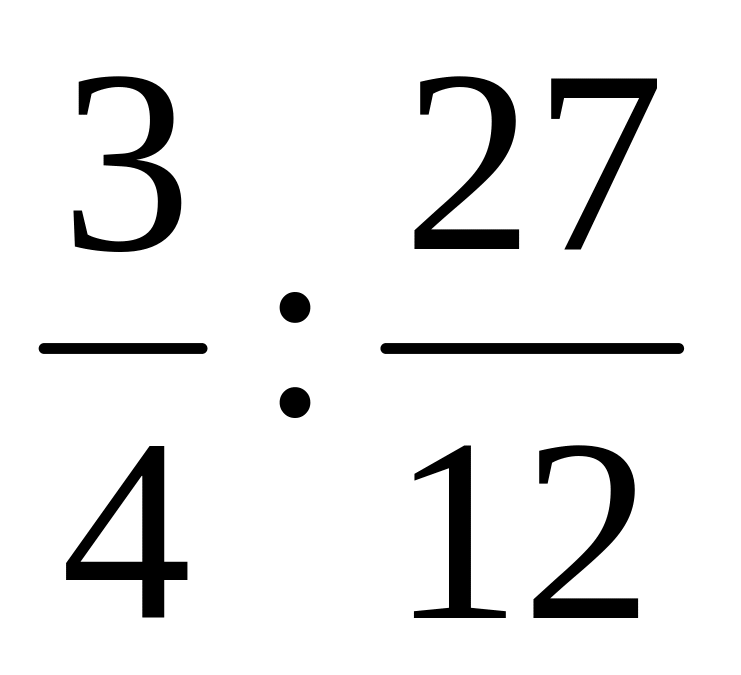 .
.Дайте определение частного положительных рациональных чисел и . Что называют операцией деления положительных рациональных чисел? Выполните деление:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]() ж)
ж)
![]() з)
з)
![]() .
.
Произведите указанные действия с рациональными числами:
а)
![]() ; б)
; б)
![]() ;
;
в)
10+![]() ; 4)
; 4)
![]() .
.
19. Выполните указанные действия:
а)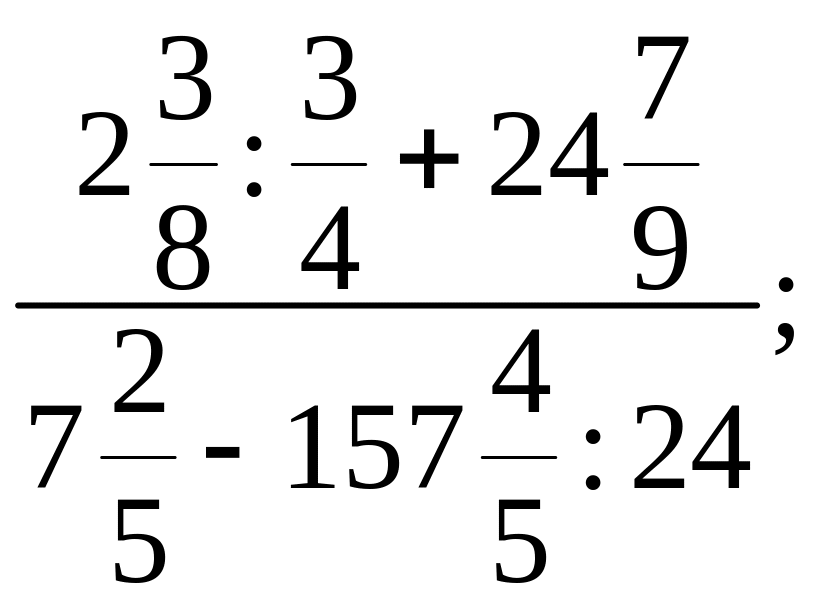 б)
б)
 .
.
Выполните указанные действия с рациональными числами:
а)
![]() ; б)
; б)
![]() .
.
