Вопросы для самопроверки
Дайте определение произведения положительных рациональных чисел.
Докажите единственность произведения положительных рациональных чисел.
Докажите, что произведение положительных рациональных чисел от выбора представителей этих чисел не зависит.
Сформулируйте определение бинарной алгебраической операции умножения положительных рациональных чисел.
Укажите свойства операции умножения на Q+.
Докажите, что
Докажите ассоциативное свойство операции умножения положительных рациональных чисел.
Докажите дистрибутивность умножения положительных рациональных чисел относительно сложения.
Докажите, что
Докажите монотонность операции умножения относительно отношений «меньше» и «больше».
Докажите, что
Докажите, что
Докажите сократимость умножения на множестве Q+ относительно отношений «равно», «меньше», «больше».
Докажите, что
2.11. Деление положительных рациональных чисел
Определение
19. Частным
от деления
положительного рационального числа
,
представленного дробью
,
на положительное рациональное число
,
представителем которого является дробь
,
является положительное рациональное
число
,
представителем которого является дробь
,
то есть
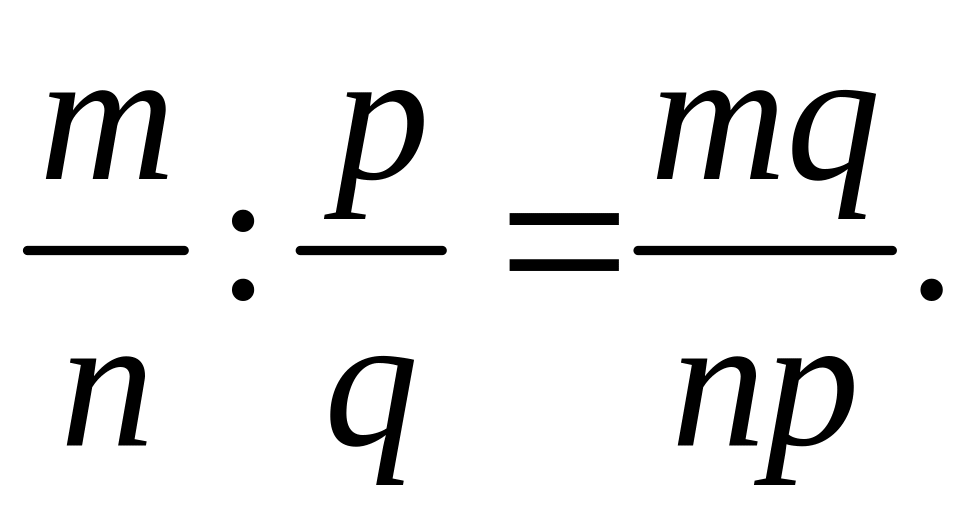
При этом числа a
и b
называются делимым
и делителем,
а число с
или
‒ частным.
Теорема 44. Частное от деления положительных рациональных чисел от выбора представителей этих чисел не зависит, то есть существует в виде единственного положительного рационального числа.
Доказательство.
Пусть a,b
− произвольные положительные рациональные
числа, выберем представителей положительных
рациональных чисел a
и b
таким образом:
.
Тогда
Умножим обе части
первого равенства на
второго – на
имеем
следовательно,
тогда
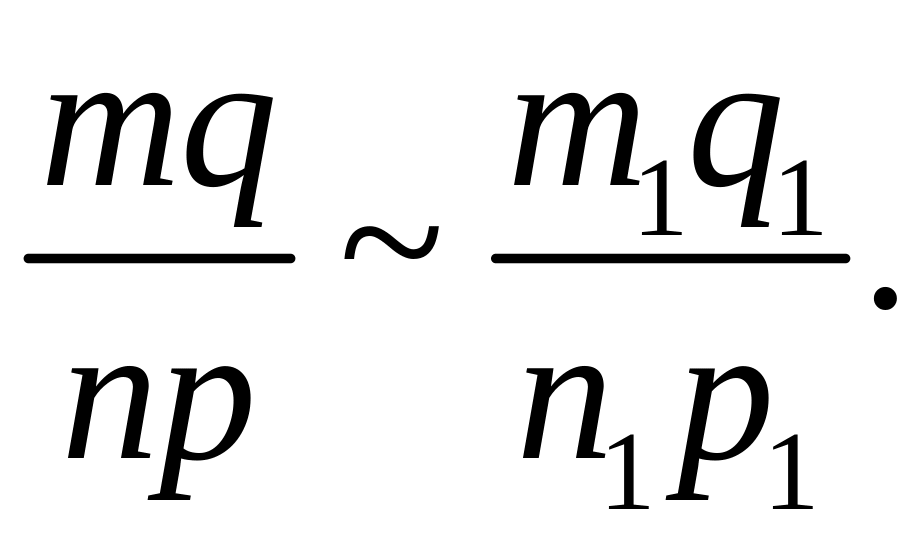Но по определению «частного»
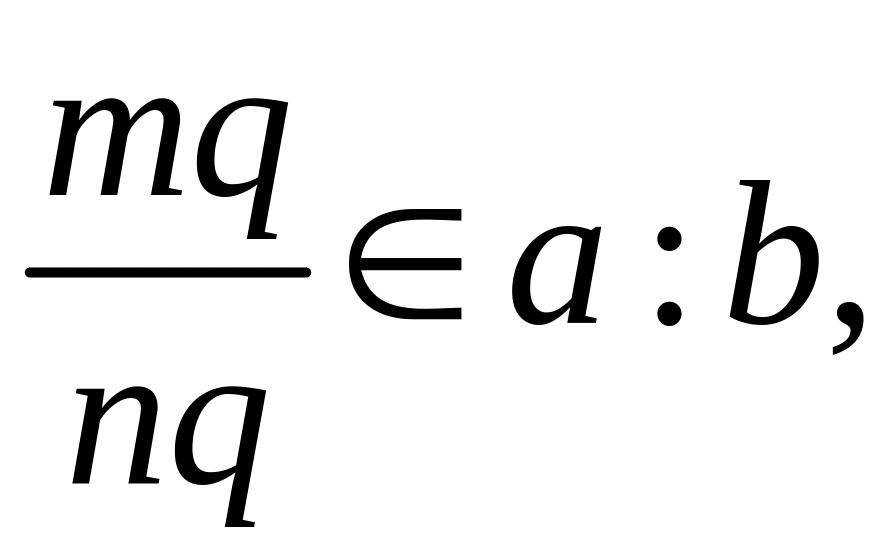
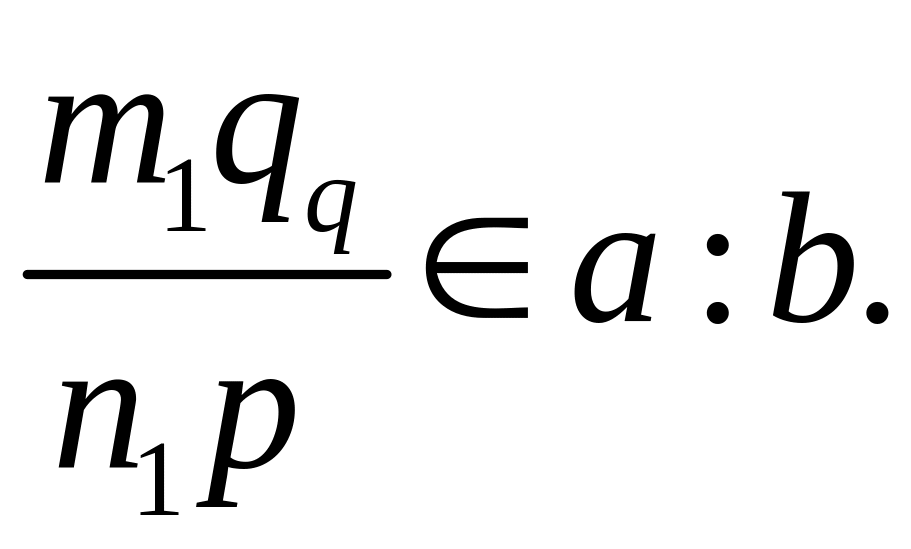
То есть дроби в
являются представителем одного и того
же числа. Теорема доказана.
2.11. Свойства операции деления
Определение 21. Делением положительных рациональных чисел называют частичную бинарную алгебраическую операцию, при которой образом пары положительных рациональных чисел является их частное от деления.
Операция деления положительных рациональных чисел неассоциативна, некоммутативна, обладает свойствами монотонности и сократимости относительно отношений «равно, больше, меньше».
Теорема 45.
Связь
умножения с делением.
Произведение частного от деления на
делитель, равно делимому, то есть
Доказательство.
Пусть
и
и
.
По определению
частного
Умножим делитель и частное, имеем:
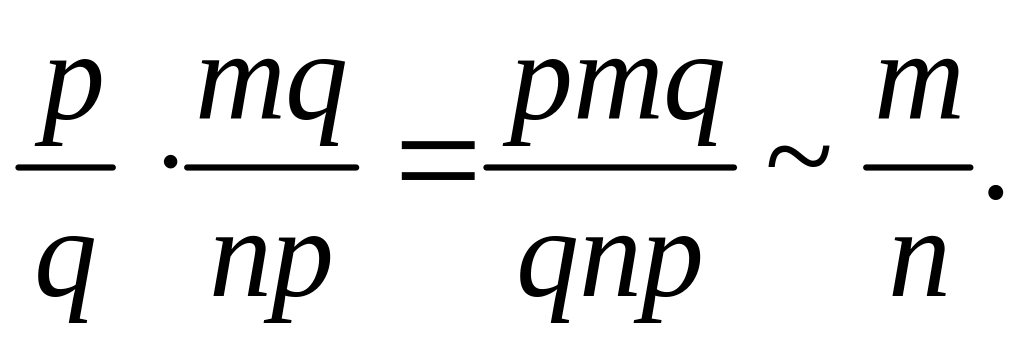Таким образом,
Теорема доказана.
Теорема 46.
Между любыми двумя различными
положительными рациональными числами
заключено бесконечно много чисел
множества, то есть
Доказательство. Рассмотрим два произвольно выбранных рациональных числа, без ограничения общности:
По условию
Рассмотрим
положительное рациональное число,
представленное дробью
Так как
Или
Итак, между любыми
двумя положительными рациональными
числами заключено хотя бы одно число
множества
.
Далее рассмотрим
числа
и
и между ними существует хотя бы одно
число из
.
Продолжая описанный процесс приходим
к выводу, что между числами
и
существует бесконечно много чисел из
.
Теорема доказана.
Теорема 47. Свойства множества . Множество бесконечное, плотное, линейно упорядоченное, счетное. В множестве нет наибольшего числа.
Доказательство.
Так как
,
следовательно, множество
является бесконечным множеством, в нем
нет наибольшего числа. Счетность
множества
следует из теоремы
46. Линейная
упорядоченность множества
следует из свойств отношений на множестве
.
Теорема Архимеда.
Для любых положительных рациональных
чисел
и
Доказательство. Рассмотрим два случая:
‒ если
тогда достаточно взять
,
в этом случае
‒ если
и
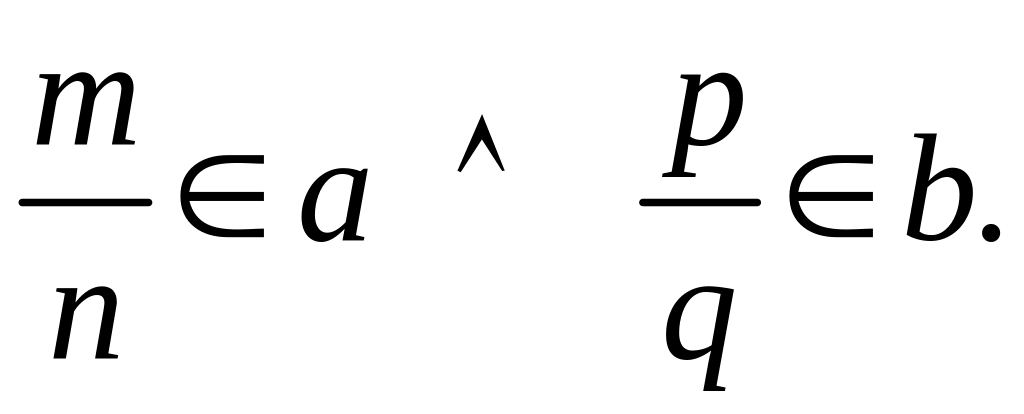
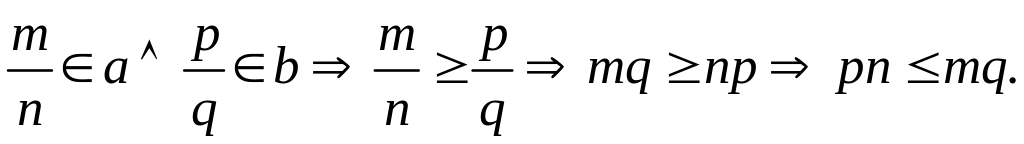
Во множестве
выполняется свойство Архимеда, то есть
Следовательно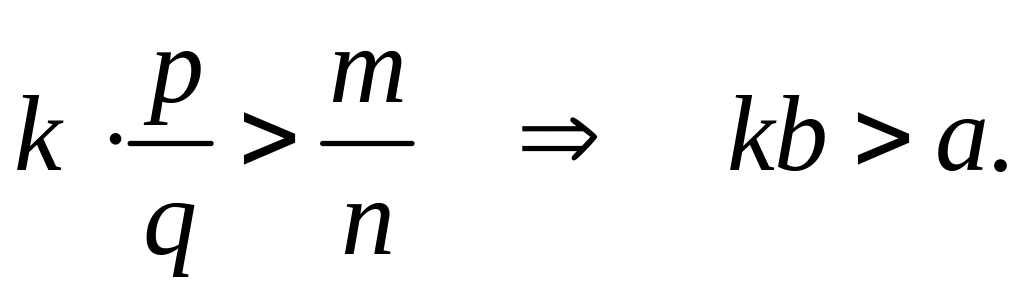
Теорема доказана.