2.6. Свойства операции сложения на

Теорема 17. Коммутативность операции сложения положительных рациональных чисел. Для любых положительных рациональных чисел справедливо: то есть

Доказательство. Пусть − произвольные положительные рациональные числа. Выберем представителей положительных рациональных чисел Докажем, что

Рассмотрим Так как Теорема доказана.

Теорема 18. Ассоциативность операции сложения положительных рациональных чисел. Для любых положительных рациональных чисел справедливо: то есть

Доказательство. Выберем представителей положительных рациональных чисел Пусть Докажем, что

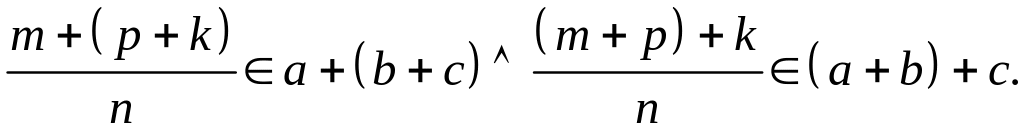
Так как то в силу ассоциативности операции сложения на , имеем

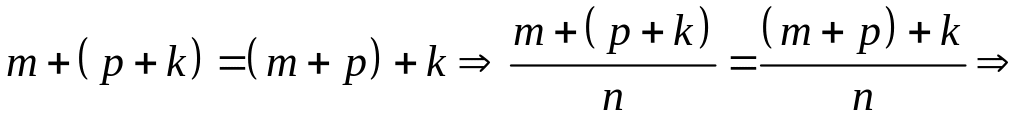
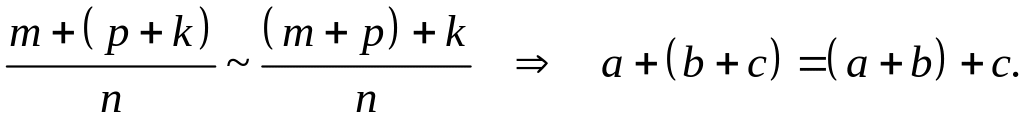Теорема доказана.

Теорема 19. Монотонность операции сложения относительно отношения равно.

Доказательство. Выберем представителей положительных рациональных чисел с одинаковыми знаменателями.

Пусть Тогда

По условию имеем

Теорема доказана.

Теорема 20. Связь операции сложения с отношением «меньше». Если рациональное число , меньше положительного рационального числа , то второе число является суммой первого числа с некоторым положительным рациональным числом , то есть

Доказательство. Выберем представителей чисел с одинаковыми знаменателями По условию

То есть найдено положительное рациональное число Теорема доказана.

Теорема 21. Монотонность операции сложения положительных рациональных чисел относительно отношения «меньше» на .

Доказательство. По условию теоремы следовательно, по теореме 20 В силу монотонности операции сложения относительно отношения «равно» имеем:

Теорема доказана.

Теорема 22. Монотонность операции сложения относительно отношения «больше» на .

Доказательство.

Теорема 23. Сократимость операции сложения положительных рациональных чисел относительно отношения «равно».

Доказательство. Докажем утверждение методом «от противного». Предположим, что но либо либо

Рассмотрим оба случая: 1) , что противоречит условию.

2) , что противоречит условию. Л И. Полученное противоречие и доказывает теорему.

Теорема 24. Сократимость операции сложения относительно отношения «меньше».

Доказательство. По условию

Теорема доказана.

Теорема 25. Сократимость операции сложения относительно отношения «больше».

Доказательство. По условию имеем

Теорема доказана.

Вопросы для самопроверки

1. Дайте определение суммы положительных рациональных чисел и .

2. Как найти сумму положительных рациональных чисел представленных дробями с одинаковыми знаменателями? Как найти сумму положительных рациональных чисел представленных дробями с различными знаменателями?

3. Докажите существование и единственность суммы положительных рациональных чисел.

4. Что называют сложением положительных рациональных чисел и ?

5. Какими свойствами обладает операция сложения на ?

6. Докажите, что операция сложения на коммутативна.

7. Докажите что сумма рациональных чисел не зависит от выбора представителей.

8. Докажите монотонность операции сложения положительных рациональных чисел относительно отношения «равно».

9. Сформулируйте теорему о связи операции сложения положительных рациональных чисел с отношением «меньше».

10. Докажите, что

11. Докажите монотонность операции сложения положительных рациональных чисел относительно отношения «больше» на .

12. Докажите сократимость операции сложения положительных рациональных чисел относительно отношения «равно».

13. Докажите, что а)
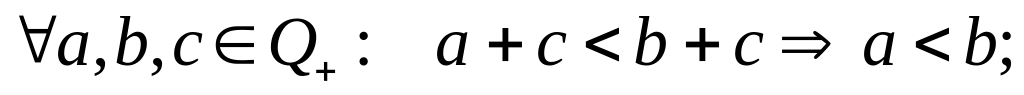