1.Основные задачи классической механики (законы Галлилея-Ньютона).Прямая и обратная задачи механики.

1.Основной закон Ньютона – равнодействующая всех сил приложенная к материальной точке прямо пропорционально её линейному ускорению и направлена в ту же сторону ,что и ускорение. R=ma

2.Закон Ньютона (первый закон Галлилео, закон инерции) – Если на мет. Точку действует уравновешенная сист. Сил ,то эта точка движется прямолинейно с постоянной по величине скоростью.

3.Закон классической механики – две мат. точки после взаимодействия движения вдоль одной прямой в противоположные стороны с ускорением обратно пропорционально их массам.

Прямая задача – определить законы движения материальной точки взаимодействующей с другими телами, если известны все силы ,действующие на неё, её начальное механическое состояние.

Обратная задача - опередить силы, действующие на мат. точку со стороны других тел, если закон движения точки известен.

2.Динамическое уравнение движения материальной точки в декартовых и естественных осях.

Алгебраическая форма динамических уравнений движения материальной точки:

Первая дифференциальная форма динамических уравнений движения точки:

;

Вторая дифференциальная форма динамических уравнений движения точки:

; ;

Динамические уравнения движения точки в естественных осях:

3.Теорема об изменении количества движения материальной точки (с выводом теоремы)

dm =Rdt Элементарное изменение кол-ва движения мат. точки равно элементар. Импульсу равнодействующей приложенной к этой точке.

Вывод формулы:

ma=R a= = R → m = Rdt

4.Теорема от изменении момента количества движения материальной точки ( с выводом теоремы)

где

Производная по времени от момента кол-ва движения мат точки относит некоторого центра равны моменту равнодейств. всех сил приложенных к относит того же центра.

5.Теорема от изменении кинетической энергии материальной точки ( с выводом теоремы)

Теорема от изменении кинетической энергии материальной точки (с выводом теоремы) (mv^2)/2-(mv_0^2)/2=А

6.Понятие работы. Теорема о работе равнодействующей силы (док-во)

dA=Fdr -Элементарная работа сил на перемещении точки его положения сил

Теорема:

Равнодействующая силы всех сил, приложенных к материальной точке, равна сумме работ всех сил действующих на эту точку на некотором перемещении.

Док-во:

Работа – это физическая величина, равная произведению силы на путь, пройденный телом под действием этой силы

7.Работа силы тяжести ( с выводом формулы)

Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот.

8.Работа силы упругости (с выводом формулы)

Работа сил упругости зависит лишь от деформаций пружины Δl1 и Δl2 в начальный и конечном состоянии.

9.Работа момента пары сил ( с выводом формулы)

10.Мощность.Коэффициент полезного действия (КПД)

Коэффициент полезного действия представляет собой отношение отдаваемой мощности к подводимой мощности.

кпд –мощность

11.Система материальных точек. Центр масс материальной системы и определение его положения.

Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы

Центр масс – точка, радиус-вектор, который определяется по формуле

12.Внешние и внутренние силы. Свойства внутренних сил системы.

Внешними называются силы, которые вызванны действием …… не входящие в систему.

Силы вызванные взаимодействием тел входящих в систему наз. внутренними. .

Свойство внутр. сил системы:

1. Геометрическая сумма всех внутр. сил системы(гл. вектор внутр. сил)=0

2.геометрическая сумма моментов всех внутр. точки пространства(гл. момент внутр. сил)=0

13.Дифференциальное уравнение движения системы материальных точек.

14.Теорема о движении центра масс ( с выводом формулы) Следствие из теоремы.

Произведение массы системы на ускорение её центра масс равна геометрической сумме всех действующих на систему внешних сил

Следствие. Если главный вектор внешних сил системы равен нулю, то центр масс М.С. либо движется с постоянной по величине и направлению скоростью, либо находится в состоянии покоя.

15. Теорема об изменении количества движения материальной системы (с выводом теоремы). Следствия из теоремы.

Следствия :

1. Внутренние силы непосредственно не влияют на изменение количества движ. Матер. Сист.

2. Если сумма всех внешних сил, действ. на сист. равна нулю, вектор колич-ва движ. матер сист остаётся постоянным по величине и направлен в течении всего времени движ.

16. Теорема об изменении момента количества движения материальной системы(с выводом теоремы). Следствия из теоремы.

Следствия :

1. Внутренние силы не влияют на изменение момента количества матер. сист

2. Если сумма моментов всех внешних сил,прилож к сист тел относит некот неподвижн центра равна нулю,то момент сист относит того же центране меняется по велич и направл ; ; ;

3. если сумма моментво всех внешн сил,прилож к сист относит некоторой неподвижной сист равна нулю,то вектор момента колич-ва движ так же не меняется по величине и направл.

17. Момент инерции материальной точки, материальной системы и твердого тела. Момент инерции сплошного однородного цилиндра, диска,стержня,тонкого кольца и тела произвольной формы.

стержня: тв. тело: ;

цилинра: ; мат. точка :

диска: 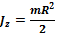; мат. система:

кольца: ; произвольной формы: ;

18. Динамические уравнения вращательного и поступательного движений твёрдого тела (с выводом формул).

вращ. Jz ε=∑M i0z^внеш

поступат.

19. Теорема об изменении кинетической энергии материальной системы( в интегральной и дифференциальной форме).

Инт форма

Диф. форма

20. Кинетическая энергия материальной системы. Теорема Кёнега (с выводом теоремы).

Кинет энергия:

Кёнега: T=((mv^2)/2)+Tотн

21. Определение кинетической энергии твёрдого тела при разных видах его движения.

1. Поступательное:

2. Вращательное:

3. Плоское:

22.Принцип Даламбера для материальной точки(с выводом формулы).

F+R+Ф=0

23.Порядок вычисления сил инерции материальной точки при движении ее по заданной криволинейной траектории и в случае если материальная точка является одной из точек вращающего тела.

Если точка движетс криволинейно траектории то ей ускорение имеет 2 сост а=а^τ+аⁿ, и силы инерции будут состоять из двух сост касат и нормали. Ф^τ=-ma^τ и Фⁿ=-maⁿ. Тогда Ф^τ=m и Фⁿ= m . Если мат точка явл одной из точки взаимод. тела Ф^τ=mεr Фⁿ= mω²r

24. Принцип Даламбера для материальной системы (с выводом формул.)

∑F+∑F +Ф =0

25.Главный вектор и главный момент сил инерции абсолютно твёрдого тела (с выводом формул).

Ф= -ma M=IE

26. Связи и их классификация.

Тело ограничивающая свободу перемещения точки, материальной системы называется связями. Она может быть записана в виде уравнений или неравенств.

Связь которая описана уравн. наз. удерживающими или двухсторонними.

Связи описыв. неравенств. наз. соответственно неудерживающими или односторонними.

Связь, уравнение или неравенство не содерж. время наз. стационарными.

Связи явно зависящие от времени наз. нестационарными.

Если уравнение поля только координаты точек и не входит их произведение, то связи наз. геометрические.

Если же в уравнение связи входит произведение от координат по времени, то связи наз. кинематические.

Связи наз. галономными, если их уравнения могут быть записаны в виде не содержащих произведения от координат по времени .

Связи наз. негалономные, если их уравнение содержат неинегр. образом произв. коэф. по времени или деференциал.