Черные и серые тела.

АБСОЛЮТНО ЧЕРНОЕ ТЕЛО - идеальное тело, полностью поглощающее всю падающую на него лучистую энергию. Излучение такого тела при любой температуре является максимальным по сравнению со всеми другими нечерными телами, а спектральное распределение излучаемой энергии зависит только от температуры и не зависит от природы тела. Для абсолютно черного тела абсолютная и цветовая температуры совпадают, вследствие чего абсолютно черное тело применяется в качестве светового эталона.

В природе не существует абсолютно черных тел, но искусственно воспроизводят весьма близкое к абсолютно черному тело в виде очень малого отверстия в закрытой полости, внутренняя поверхность которой обладает весьма значительным поглощением. Любой луч, попавший в отверстие, поглощается полностью после нескольких отражений от стенок полости.

Абсолютно черное тело позволяет установить законы излучения температурных источников света.

Рис. 1. Модель абсолютно черного тела

СЕРОЕ ТЕЛО - тело, поглощения коэффициент к-рого меньше 1 и не зависит от длины волны излучения  и абс. темп-ры Т. Коэф. поглощения  (наз. также коэф. черноты С. т.) всех реальных тел зависит от  (селективное поглощение) и Т, поэтому их можно считать серыми лишь в интервалах  и Т, где коэф.  прибл. постоянен. В видимой области спектра свойствами С. т. обладают каменный уголь (  = 0,80 при 400- 900 К), сажа (  = 0,94-0,96 при 370-470 К); платиновая и висмутовая черни поглощают и излучают как С. т. в наиб. широком интервале  - от видимого света до 25-30 мкм (  = 0,93-0,99).

С. т. является источником т. н. серого излучения - теплового излучения, одинакового по спектральному составу с излучением абсолютно чёрного тела, но отличающегося от него меньшей энергетич. яркостью .К серому излучению применимы законы излучения абсолютно чёрного тела - Планка закон излучения, Вина закон излучения, Рэлея - Джинса закон излучения. Понятие С. т. применяется в пирометрии оптической.

2. Законы теплового излучения. Закон Ст.-Больцмана.

Любое нагретое тело излучает электромагнитные волны. Чем выше температура тела, тем более короткие волны оно испускает. Тело, находящееся в термодинамическом равновесии со своим излучением, называют абсолютно черным (АЧТ). Излучение абсолютно черного тела зависит только от его температуры. В 1900 году Макс Планк вывел формулу, по которой при заданной температуре абсолютно черного тела можно рассчитать величину интенсивности его излучения.

Австрийскими физиками Стефаном и Больцманом был установлен закон, выражающий количественное соотношение между полной излучательной способностью и температурой черного тела:

ε = σT4.

Этот закон носит название закон Стефана–Больцмана. Константа σ = 5,67∙10^–8 Вт/(м²∙К⁴) получила название постоянной Стефана–Больцмана.

Все планковские кривые имеют заметно выраженный максимум, приходящийся на длину волны

Этот закон получил название закон Вина. Так, для Солнца Т₀ = 5 800 К, и максимум приходится на длину волны λ_max ≈ 500 нм, что соответствует зеленому цвету в оптическом диапазоне.

С увеличением температуры максимум излучения абсолютно черного тела сдвигается в коротковолновую часть спектра. Более горячая звезда излучает большую часть энергии в ультрафиолетовом диапазоне, менее горячая – в инфракрасном.

3. Закон смещения Вина.

  В 1893 году немецкий ученый Вильгельм Вин рассмотрел задачу об адиабатическом сжатии излучения в цилиндрическом сосуде с зеркальными стенками и подвижным зеркальным поршнем. При движении поршня энергия излучения единицы объема (плотность энергии) будет возрастать по двум причинам:

•         за счёт уменьшения объема (общая величина энергии постоянна);

•         за счёт работы, совершаемой поршнем против давления излучения.

      Однако, в силу эффекта Доплера (увеличение частоты излучения, отраженного от движущегося поршня) движение поршня приводит к изменению частоты излучения. Окончательно Вин получил:

где  и  – постоянные, которые Вин не расшифровал.

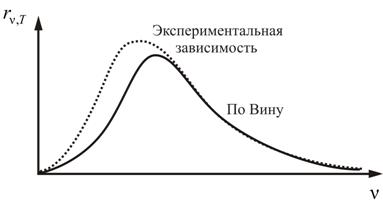
      Эта формула дает хорошее согласие с опытом в коротковолновой части спектра и не годится для длинноволновой (рис.1.4).

Выражение (1.4.1) имеет сейчас лишь историческую ценность. Но Вин нашел зависимость  – частота соответствующая максимальному значению абсолютно черного тела). Найдем максимум функции (1.4.1), то есть производную по ν и приравняем к нулю.

Это и есть закон смещения Вина. Смещение частоты в зависимости от температуры хорошо иллюстрируется экспериментальными кривыми, изображенными на рис. 1.3.

      Чаще закон смещения Вина записывают в виде   где постоянная Вина  (За работы по тепловому излучению Вин в 1910 году получил Нобелевскую премию).

Современные теории строения материи 1. Фотоэффект.

Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

Законы фотоэффекта:

Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока.

Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от егоинтенсивности.

3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света   (или максимальная длина волны λ₀), при которой ещё возможен фотоэффект, и если  , то фотоэффект уже не происходит.

Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода φ, покидает металл:   где   — максимальная кинетическая энергия, которую имеет электрон при вылете из металла.

Фотоэффектом (или внешним фотоэффектом) называют испускание электронов поверхностью твёрдых или жидких тел под действием света. Фотоэффект, открытый немецким физиком Г. Герцем, можно наблюдать с помощью установки, показанной на рис. 30а. В стеклянную колбу К помещают два электрода (1 и 2) и создают вакуум, при этом через окошко О колбы на электрод 1 падает поток света. Свет, падающий на электрод 1, вырывает из его поверхности электроны (фотоэлектроны), движение которых зависит от электрического поля между электродами. Если напряжение U между электродами 1 и 2 (отсчитываемое от потенциала электрода 1) положительно, то фотоэлектроны полетят к электроду 2, образуя ток (фототок), регистрируемый гальванометром Г.

Зависимость силы фототока I от напряжения U между электродами (см. чёрную кривую на рис. 30б) показывает, что при росте U сила фототока сначала увеличивается, а потом, достигая максимума, перестаёт расти. Максимальное значение силы фототока называют током насыщения I_н. Измеряя ток насыщения, можно вычислить, сколько фотоэлектронов каждую секунду вырываются из освещаемого электрода. При отрицательных U сила фототока уменьшается, т.к. электрическое поле тормозит фотоэлектроны, и до электрода 2 долетают только те, кинетическая энергия которых больше  . На рис.30б видно, что при напряжении, меньшем U_з,  фототок отсутствует. U_З  называют запирающим (или задерживающим) напряжением и его величина следующим образом связана с максимальной кинетической энергией Е_макс фотоэлектронов:

Е_макс =   .       

2. Опыты Столетова.

3. Законы внешнего фотоэффекта. Одно- и двухэлектронная теория.

Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

Законы фотоэффекта:

Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока.

Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от егоинтенсивности.

3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света   (или максимальная длина волны λ₀), при которой ещё возможен фотоэффект, и если  , то фотоэффект уже не происходит.

4. Фотон. Энергия, масса и импульс фотона.

В 1905 г. Эйнштейн выдвинул смелую идею, обобщавшую гипотезу квантов, и положил ее в основу новой теории света (квантовой теории фотоэффекта). Согласно теории Эйнштейна, свет с частотой νне толькоиспускается, как это предполагал Планк, но и распространяется и поглощается веществом отдельными порциями (квантами), энергия которых  . Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью распространения света в вакууме (с). Квант электромагнитного излучения получил название фотон.

5. Формула Эйнштейна для фотоэффекта.

Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

В опытах были установлены три закона фотоэффекта:

1. Сила фототока прямо пропорциональна плотности светового потока. Для сравнения на рис. 30б синей кривой показана зависимость фототока от напряжения для большей плотности светового потока.

2. Максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой  света (см. рис. 30в) и не зависит от плотности светового потока.

3. Для каждого вещества существует наименьшая частота света _мин, ниже которой фотоэффект не происходит (см. _мин на рис. 30в), называемая красной границей фотоэффекта.

Законы фотоэффекта не удаётся объяснить с помощью законов классической физики, которую мы изучали до сих пор. Для их объяснения А. Эйнштейн в 1905 использовал идею, высказанную ранее немецким физиком М. Планком, согласно которой свет – поток частиц, фотонов. При этом энергия E каждого фотона, называемая квантом, равна:

E=h,                                                        (30.2)

где - частота света, а h – коэффициент, названный постоянной Планка и равный 6,63^.10^-34 Дж^.с.

Эйнштейн предположил, что фотон может выбить с поверхности только один электрон, а электрону, чтобы вырваться из вещества, необходимо совершить работу выхода А_вых. Тогда из закона сохранения энергии следовало, что при фотоэффекте энергия фотона h должна быть равна сумме работы выхода А_вых и кинетической энергии фотоэлектрона со скоростью v и массой m:

Уравнение (30.3), объясняющее все законы фотоэффекта, называют уравнением Эйнштейна для фотоэффекта. Чем больше фотонов, тем больше они выбивают фотоэлектронов. Это и является объяснением закона №1 фотоэффекта. Согласно (30.3) кинетическая энергия фотоэлектронов прямо пропорциональная частоте света и не зависит от его интенсивности, что и объясняет закон №2 фотоэффекта. Из уравнения (30.3) следует, что фотоэлектрону необходимо совершить работу выхода А_вых, и свет с частотой меньше _мин = А_вых/h не будет вызывать фотоэффекта, что и объясняет закон №3 фотоэффекта. 

6. Экспериментальное подтверждение теории Эйнштейна для фотоэффекта.

Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

Уравнение Эйнштейна было подтверждено опытами Милликена. В его приборе (1916 г.) поверхность исследуемого металла подвергалась очистке в вакууме. Ис­следовалась зависимость максимальной кинетической энергии фотоэлектронов (изме­нялось задерживающее напряжение U₀ (см. (202.1)) от частоты  и определялась постоянная Планка. В 1926 г. российские физики П. И. Лукирский (1894—1954) и С. С. Прилежаев для исследования фотоэффекта применилиметод вакуумного сферического конденсатора. Анодом в их установке служили посеребренные стенки стеклянного сферического баллона, а катодом — шарик (R 1,5 см) из исследуемого металла, помещенный в центр сферы. В остальном схема принципиально не отличается от описанной на рис. 289. Такая форма электродов позволила увеличить наклон вольт-амперных характеристик и тем самым более точно определять задерживающее напряжение U₀ (а следовательно, и h). Значение h, полученное из данных опытов, согласуется со значениями, найденными другими методами (по излучению черного тела и по коротковолновой границе сплошного рентгеновского спектра). Все это является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта.

Если интенсивность света очень большая (лазерные пучки), то возможен многофотонный (нелинейный) фотоэффект, при котором электрон, испускаемый метал­лом, может одновременно получить энергию не от одного, а от N фотонов (N=27). Уравнение Эйнштейна для многофотонного фотоэффекта

 Наиболее непосредственное подтверждение гипотезы Эйнштейна дал опыт Боте, в котором использовался метод совпадения (рис. 2.4).

Рис. 2.4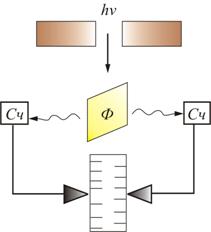

      Тонкая металлическая фольга Ф помещалась между двумя газоразрядными счетчиками Сч. Фольга освещалась слабым пучком рентгеновских лучей, под действием которых она сама становилась источником рентгеновских лучей (это явление называется рентгеновской флуоресценцией). Вследствие малой интенсивности первичного пучка, количество квантов, испускаемых фольгой, было невелико. При попадании квантов на счетчик механизм срабатывал и на движущейся бумажной ленте делалась отметка. Если бы излучаемая энергия распространялась равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении. Так было экспериментально доказано существование особых световых частиц – фотонов.

7. Корпускулярно-волновая двойственность частиц света.

физический принцип, утверждающий, принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантованных полей в квантовой теории поля.

Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных волн. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла^[1].

Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей, что наглядно показал эксперимент, проведённый французскими физиками Гранжье, Роже и Аспэ в 1986 году^[2]. Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).

В настоящий момент концепция корпускулярно-волнового дуализма представляет лишь исторический интерес, так как служила только интерпретацией, способом описать поведение квантовых объектов, подбирая ему аналогии из классической физики. На деле квантовые объекты не являются ни классическими волнами, ни классическими частицами, приобретая свойства первых или вторых лишь в некотором приближении. Методологически более корректной является формулировка квантовой теории через интегралы по траекториям (пропагаторная), свободная от использования классических понятий.

8. Волна де Бройля.

волны, связанные с любыми микрочастицами и отражающие их волновую природу.

Впервые квантовые свойства были открыты у эл--магн. поля. После исследования M. Плавком (M. Planck) законов теплового излучения тел (1900) в науку вошло представление о "световых порциях" - квантах эл--магн. поля. Эти кванты - фотоны-во многом похожи на частицы (корпускулы): они обладают определёнными энергией и импульсом, взаимодействуют с веществом как целое. В то же время давно известны волновые свойства эл--магн. излучения, к-рые проявляются, напр., в явлениях дифракции и интерференции света. T. о., можно говорить о двойственной природе, или о корпускулярно-волновом дуализме, фотона.

В 1924 Л. де Бройль (L. de Broglie) высказал гипотезу о том, что корпускулярно-волновой дуализм присущ всем без исключения видам материи - электронам, протонам, атомам и т. д., причём количественные соотношения между волновыми и корпускулярными свойствами частиц те же, что и установленные ранее для фотонов. А именно, если частица имеет энергию и импульс, абс. значение к-рого равно р, то с ней связана волна частоты и длины , где 6*10^-27 эрг*с - постоянная Планка. Эти волны и получили назв. В. де Б.

Для частиц не очень высокой энергии , где - масса и скорость частицы. Следовательно, длина В. де Б. тем меньше, чем больше масса частицы и её скорость. Напр., частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует В. де Б. с 10^-18 , что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопич. тел. Для электронов с энергиями от 1 эВ до 10 000 эВ длины В. де Б. лежат в пределах от 10 до 0,1 , т. е. в интервале длин волн рентг. излучения. Поэтому волновые свойства электронов должны проявиться, напр., при их рассеянии на тех же кристаллах, на к-рых наблюдается дифракция рентгеновских лучей.

9. Принцип неопределенности Гейзенберга.

фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределённостей^{[* 1]} задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых.

Соотношение неопределенностей Гейзенберга

фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых, описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля)

1. Дифракция на круглом отверстии.

Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),

где знак плюс соответствует нечетным m и минус — четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсив­ность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А₁, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки Вбудет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непроз­рачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то А_m<<A₁ и результирующая амплитуда A=A₁/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблю­дается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.

2. Дифракция на круглом диске. Зонная пластинка.

5. Дифракция на пространственной решетке. Рентгеновская спектроскопия. Рентгеноструктурный анализ.

Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат.

      Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называютодномерной.

      Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумы двумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток:

      где φ  - угол между направлением на главный максимум (направление луча) и нормалью к решетке;  m – порядок дифракционного максимума.

Рентгеновская спектроскопия получение рентгеновских спектров испускания и поглощения и их применение к исследованию электронной энергетической структуры атомов, молекул и твёрдых тел. К Р. с. относят также рентгено-электронную спектроскопию, т. е. спектроскопию рентгеновских фото- и оже-электронов, исследование зависимости интенсивности тормозного и характеристического спектров от напряжения на рентгеновской трубке (метод изохромат), спектроскопию потенциалов возбуждения.

Рентгенострукту́рный ана́лиз (рентгенодифракционный анализ) — один из дифракционных методов исследования структуры вещества. В основе данного метода лежит явление дифракциирентгеновских лучей на трехмерной кристаллической решётке.