2.2.3. Метод евристичного пошуку
Алгоритм упорядкованого перебору
Для більшості задач вдається сформулювати емпіричні правила, що дозволяють зменшити об’єм перебору. Ці правила використовують інформацію про задачу.
Основна ідея евристичних алгоритмів полягає в упорядкування списку вершин у відповідності з певною мірою, що оцінює перспективність вершини або шляху, на якому знаходиться вершина.
Таку міру називають оціночною функцією.
Алгоритм:
Помістити початкову вершину в перелік ВДК.
Якщо перелік ВДК пустий, то повідомити про невдачу, інакше перейти до кроку 3.
Взяти першу вершину із списку ВДК і перенести її у список ЗКР, присвоїти вершині ідентифікатор v.
Розкрити вершину v. Помістити усі дочірні вершини (ті, що не повторюються), тобто що не зустрічаються у переліку ЗКР, у кінець списку ВДК і побудувати вказівники, що ведуть від них до вершини .
Якщо вершина не має дочірніх вершин або має тільки повторювані дочірні вершини, то перейти до кроку 2.
Перевірити, чи не є одна з дочірніх вершин цільовою. Якщо є, то видати рішення, в іншому випадку перейти до кроку 2.
У цьому алгоритмі передбачається, що початкова вершина не може бути цільовою. Алгоритм дозволяє знайти оптимальне рішення. Маючи граф станів і порівнюючи відстані різних маршрутів, що ведуть до цільових, можна обрати оптимальні маршрути.
2.3. Методи пошуку рішень інтелектуальної задачі у разі зведення задач до підзадач
Пошук рішення при даному типі представлення задачі спирається на граф редукції.
Побудова графа редукції задачі аналогічно побудові графа пошуку рішень у просторі станів.
Ціль пошуку – показати, що початкова вершина вирішувана. Процедуру пошуку можна інтерпретувати як побудову дерева рішень.
Дерево рішення – піддерево графа редукції, що складається з вирішуваних вершин.
Пошук на графі редукції відрізняється від пошуку на графі станів тим, що включає процедури перевірок вирішуваності і невирішуваності вершин замість процедур перевірок відповідності стану цільовому.
Вершина невирішувана, якщо вона є тупиковою і якщо не вирішувані усі її дочірні вершини, коли вони пов’язані відношенням АБО і хоча б одна з її дочірніх вершин, коли вони пов’язані відношенням І.
Також розрізняють методи:
1.Сліпого перебору.
2.Впорядкованого перебору.
До першого належить метод повного перебору, до другого належать евристичні методи пошуку.
Для впорядкування вершин, що розкриваються, на дереві І-АБО використовується оптимальне потенціальне дерево рішення для виокремлення якого застосовується евристична функція.
У процесі пошуку евристична функція визначалася як оцінка вартості оптимального шляху від заданої вершини до цільової.
У деревах І-АБО для її визначення використовується оцінка вартості дерева рішень.
Алгоритм повного перебору
У методі повного перебору вершини розкриваються у тому порядку, в якому вони будуються.
Помістити початкову вершину S0 у перелік ВДК.
Взяти першу вершину із переліку ВДК і помістити її у перелік ЗКР, позначити цю вершину через .
Розкрити вершину і помістити всі її дочірні вершини в кінець списку ВДК і провести від них вказівники до вершини .
Якщо дочірніх вершин не виявилося, то помітити вершину як не вирішувану і перейти до наступного кроку, інакше перейти до кроку 7.
Застосувати до дерева пошуку процедуру розмітки невирішуваних вершин.
Якщо початкова вершина позначена як невирішувана, то видати результат про невдачу, інакше перейти до наступного кроку.
Вилучити зі списку ВДК усі вершини, що мають невирішені передуючі їм вершини, і перейти до кроку 2.
Якщо дочірні вершини є зв’язаними, то перейти до наступного кроку, інакше перейти до кроку 9.
Якщо всі дочірні вершини є заключними, то позначити як розв’язувану і перейти до кроку 10, інакше - як нерозв’язувану і іти до кроку 4.
Якщо хоча б одна дочірня вершина є заключною, то позначити як вирішувану й іти до кроку 10, інакше – як нерозв’язувану і перейти до кроку 4.
Зробити розмітку розв’язуваних вершин.
Якщо початкова вершина позначена як розв’язувана, то вивести дерево рішення, інакше перейти до наступного кроку.
Вилучити із переліку ВДК усі вершини , що є розв’язуваними, або ті, що мають розв’язувані передуючі їм вершини і перейти до кроку 2.
Рис. 2.7. Пошукове дерево редукції задачі
На рисунку наведений приклад пошукового дерева редукції задачі, на вершинах наведені цифри, що вказують послідовність розкриття вершин. Літерою z позначені заключні вершини. Дерево рішень виділено жирною лінією. Вершини А і В не розкриті, бо є тупиковими. Вершини C і D можуть бути не тупиковими і не заключними. Але вони не розкриті, бо після розкриття вершини 10 знайдено вирішуване дерево і алгоритм повного перебору закінчує роботу.
Алгоритм перебору в глибину
При методі перебору в глибину відшукується дерево рішень у межах заданої граничної глибини і кожен раз розкривається та з вершин , що побудована останньою, з глибиною, яка строго менше граничної глибини.
Якщо вирішувальне дерево містить вершини з глибиною, яка перевищує граничну глибину, природно, що рішення не буде знайдене.
Помістити початкову вершину S0 в перелік ВДК.
Взяти першу вершину із переліку ВДК і помістити її у перелік ЗКР, позначити цю вершину через .
Якщо глибина вершини дорівнює граничній глибині, то позначити вершину як невирішувану і перейти до кроку 5, інакше перейти до наступного кроку.
Розкрити вершину . Помістити усі дочірні вершини ( у будь-якому порядку) у початок переліку ВДК і провести від них показники до вершини .
Якщо дочірніх вершин немає, то помітити вершину як нерозв’язувану і перейти до наступного кроку, інакше перейти до кроку 8.
Застосувати до дереву пошуку процедуру розмітки не вирішуваних вершин.
Якщо початкова вершина позначена як невирішувана, то видається результат про невдачу, інакше перейти до наступного кроку.
Вилучити із переліку ВДК усі вершини, що мають не вирішувані передуючі їй вершини. Перейти до кроку 2.
Якщо дочірні вершини є зв’язаними, то перейти до наступного кроку, інакше перейти до кроку 10.
Якщо всі дочірні вершини є заключними, то позначити як вирішувану і перейти до 11, інакше – як не вирішувану і перейти до 5.
Якщо хоча б одна дочірня вершина є заключною, то позначити як вирішувану і йти до 11, інакше – як не вирішувану і перейти до 5.
Застосувати до дерева перебору процедуру розмітки вирішуваних вершин.
Якщо початкова вершина позначена як вирішувана, то виводиться дерево рішення, інакше перейти до наступного кроку.
Вилучити зі списку ВДК усі вершини, що є вирішуваними, або ті,що мають вирішувані передуючі їм вершини, і перейти до кроку 2.
На рисунку наведено пошукове дерево редукції, яке будується при переборі в глибину з граничною глибиною 4.
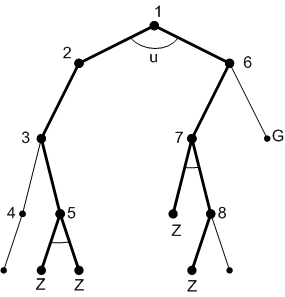
Рис.2.8. Пошукове дерево редукції