Розділ 3 моделювання управління портфелем цінних паперів пат кб «приватбанк»

3.1. Побудова економіко-математичної моделі управління портфелем цінних паперів пат кб “ПриватБанк”

У реальності прибутковості цінних паперів залежать від факторів фінансового ринку. У ролі провідного чинника фінансового ринку найзручніше брати середню прибутковість ризикових паперів самого фінансового ринку.

Позначимо цей чинник як f і будемо вважати, що дохідності всіх цінних паперів залежать від нього. Нехай d – дохідність будь-якої фіксованої цінного паперу. Найпростіша форма залежності – лінійна, так що приймемо гіпотезу, що d лінійно залежить від f ^d≈a+bf. Так як обидві величини d, f – випадкові, то рівність навряд чи може бути точним. Знайдемо a і b.

Спробуємо підібрати таку залежність 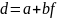, щоб F_(a,b) = M [(D-a-bF)²] було мінімальним. Маємо:

F_(a,b) = M [(D²-2aD-2bFD+a²+2abF+b²F²]=

=M[D²]-2aM[D]-2bM[FD]+a²+2abM[X]+b²M[F²] (3.1)

Диференціюючи F(a,b) приватно по а і b прирівнюємо приватні похідні 0, отримаємо систему рівнянь:

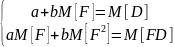
Вирішуючи цю систему, одержимо:

b= K_FD / D_F ,

a=M[D]-M[F]/ K_FD / D_F (3.2)

Знайдемо математичне сподівання випадкової величини Z=M[D]+(F-M[F]/ K_FD / D_F ), що є функцією від випадкової величини D. Маємо M[Z]= M[D]. Значить, зокрема, при знайдених a, b для математичних очікувань випадкових величин D, F вірно не наближене рівність, а точніше:

M[D]=a+bM[F].

На практиці спільний розподіл випадкових величин (F, D) не відомо, відомі тільки результати спостережень, тобто вибірка пар (f, d) значень (F, D). всі розглянуті величини замінюються їх вибірковими аналогами. Так, для визначення a, b отримаємо систему рівнянь:

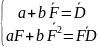(3.3)

Вирішуючи цю систему, одержимо 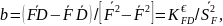значить, пряма лінія регресії має рівняння 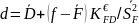. Через 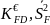позначимо вибіркові аналоги кореляційного моменту випадкової величини F, D і дисперсії F відповідно.

Також можна переконатися, що для середніх арифметичних значень вірно точне рівність, тобто D = a + b .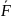

Зазвичай замість літери b_i використовують букву 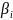. Цей коефіцієнт так і називають “бета цінних паперів i – ого виду щодо ринку. Ця величина визначає вплив ринку на дані цінні папери: якщо 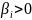, то прибутковість паперів i - ого виду коливається в такт з ринком, а якщо 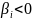, то поведінка папери прямо протилежно коливань прибутковості ринку в цілому.

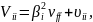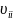Варіація доходності кожного цінного паперу дорівнює тобто складається з двох доданків: “власної” варіації , що не залежить від ринку, і “ринкової” частини варіації 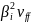, яка визначається випадковим поведінкою ринку в цілому. Їхнє ставлення 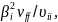позначається 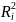і називається R-squared. Це відношення характеризує частку ризику даних цінних паперів, що вноситься ринком ті папери, для яких R-squared велике, в якомусь сенсі краще, так як їх поведінка більш передбачувано.

Знайдемо параметри лінійної регресії за вибіркою ТОВ “Центренерго”, представленої в табл. 3.1. Зобразимо дані та регресійну залежність між ними на графіках (рис. 3.1). Результати розрахунків представлені в додатку А.

Таблиця 3.1