3.2. Оцінка результатів та застування економіко-математичної моделі управління портфелем цінних паперів пат кб “ПриватБанк”
Основна мета: вибір і покупка портфеля цінних паперів, який би задовольняв усіх експертів банку.
Складність полягає в тому, що різні фактори і показники мають різну квалиметрической основу і мають різну розмірність.
МАІ при побудові єдиної шкали для різних компонент проблеми використовує міру (ступінь) впливу кожного фактора одного рівня на фактори верхнього рівня на кінцеву мету. Цей захід утворюється в результаті висловлювання суджень про ступінь впливу (важливості цих чинників).
Відомий американський фахівець з системного аналізу Т. Сааті запропонував шкалу відносної важливості (значущості, переваги), подану в табл. 3.11.
Таблиця 3.11
Шкала відносної важливості Сааті
Визначення переваги одного об'єкта над іншим |
Міра важливості, значущості переваги |
Рівна важливість (значущість). Ні переваги |
1 |
Слабка перевага по важливості (значимості) Слабке перевагу |
3 |
Істотне або сильне перевага по важливості (значимості). Сильне перевагу |
5 |
Дуже сильне або значну перевагу по важливості (значимості). Дуже сильне перевагу. |
7 |
Абсолютна перевага. Абсолютна перевага |
9 |
Проміжна оцінка міри важливості між сусідніми значеннями. |
2,4,6,8 |
Вибір дев'яти бальної шкали заснований на психометричних властивості людини, які добре дозволяють проводити якісні порівняння властивостей об'єктів за такими рівнями: нема різниці, слабке відмінність, сильне розходження, дуже сильне розходження, абсолютна відмінність. Враховуючи компромісні оцінки, отримуємо дев'ять ступенів відмінності. Крім того, в психології існує поняття психологічного межі, здатності людини одночасно розрізняти якесь число меж з якого-небудь властивості. Ця межа дорівнює 7 ± 2, тобто для створення шкали, за якою ці межі будуть розрізняється, необхідно 9 точок.
Для цих цілей застосовуються метод парних порівнянь. Якщо для порівняння вибрано n (А 1, А 2, ..., А n) об'єктів, то результати порівнянь заносяться в квадратну n – мірну матрицю виду (табл. 3.12):
Таблиця 3.12
Матриця парних порівнянь
|
A 1 |
A 2 |
... |
A j |
... |
A n |
А 1 |
a 11 |
a 12 |
... |
a 1j |
... |
a 1n |
А 2 |
a 21 |
a 22 |
... |
a 2j |
... |
a 2n |
... |
... |
... |
... |
... |
... |
... |
А i |
a i1 |
a i2 |
... |
a ij |
... |
a in |
... |
... |
... |
... |
... |
... |
... |
А n |
a n1 |
a n2 |
... |
a nj |
... |
a nn |
Елементом
цієї матриці а
ij
є міра переваги А
i
об'єкта в порівнянні з Аj
об'єктом. Таким чином, i-й
рядок матриці показує міру переваги
i-го
об'єкта над іншими (n-1)
об'єктами n над самим собою. Міра переваги
виражається експертом в шкалі Сааті і
приймає значення від 1 до 9, якщо об'єкт
Аi
краще або більш важливий ніж об'єкт
Аj
. У випадку,
коли i = j,
міра переваги дорівнює 1, тобто
діагональні елементи матриці парних
порівнянь завжди дорівнюють 1. Слід
враховувати, що для матриці парних
порівнянь виконуються наступні умови:
.
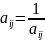Це
означає, що якщо за шкалою Сааті об'єкт
А i
краще A j
і а ij
= 5, у міру переваги А
j
об'єкта по відношенню до А
i
тобто
Таким чином, експертом заповнюється тільки верхня над діагональна частина матриці парних порівнянь (заштрихована) і матриця набуває наступний вигляд (наприклад для чотирьох порівняльних об'єктів) (табл. 3.13):
Таблиця 3.13