- •6. Модели управления запасами
- •I этап. Условная оптимизация
- •.1.3. Задача о раскрое
- •Аналогичные равенства можно записать и для всех остальных видов изделий, т.Е. Условие комплектности приводит к системе ограничений:
- •Очевидно,
- •(На раскрой поступает a единиц сырьевого материала), а также
- •При ограничениях:
- •Которую называют двойственной к задаче оптимального выпуска продукции из имеющихся ресурсов.

Экзамен. Методы математического программирования.
Теория.
Математическая модель — это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики
Математическое моделирование- процесс построения и изучения математических моделей.
Признаки классификации |
Виды математических моделей |
1. Принадлежность к иерархическому уровню |
|
2. Характер взаимоотношений со средой |
|
3. Характер отображаемых свойств объекта |
|
4. Способ представления свойств объекта |
|
5. Способ получения модели |
|
6. Причинная обусловленность |
|
7. По отношению к времени |
|
8. По типу уравнений |
|
9. По множеству значений переменных |
|
10. По назначению |
|
Математическое программирование- математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами).
Методы решения задач:
М-метод.
Симплекс-метод
Метод искусственного базиса
Метод северо-западного угла.
Метод потенциалов
Динамическое программирование- раздел математики, посвящённый теории и методам решения многошаговых задач оптимального управления.
Сетевое планирование и управление - система планирования и управления разработкой крупных народно-хозяйственных комплексов научными исследованиями конструкторской и технологической подготовкой производства новых видов изделий.
Имитационное моделирование (ситуационное моделирование) — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности.
Математические основы прогнозирования. Аппроксимация. Интерполяция.
Интерполя́ция— способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Аппроксимация -замена одних математических объектов другими, в том или ином смысле близкими к исходным.
6. Модели управления запасами
Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени. Для обеспечения непрерывного и эффективного функционирования практически любой организации необходимо создание запасов. В любой задаче управления запасами требуется определить количество заказываемой продукции и сроки размещения заказов.
GPSS (англ. General Purpose Simulation System — система моделирования общего назначения) — язык моделирования, используемый для имитационного моделирования различных систем, в основном систем массового обслуживания.
ТЕОРИЯ ДВОЙСТВЕННОСТИ .
Каждой задаче Л.П. можно поставить в соответствие двойственную задачу , решения которой дает немедленное решение прямой задачи
Теорема двойственности
Если прямая и двойственная задача имеют допустимые решения Х и У , то они имеют оптимальное решение Х* и У* и причем значение функции в этих точках совпадают. Zmax=Wmin
Практическая часть
Пример 1
Имеются стержни длиной 5 м. Необходимо их разрезать на заготовки 2-х видов: А – длиной 1,5 м; В – длиной 0,8 м для производства 20 изделий. На каждое изделие требуется две длинных заготовки (А) и три коротких (В). Определить число стержней, которое необходимо разрезать каждым из возможных способов, чтобы изготовить нужное число изделий и минимизировать отходы.
Решение
Прежде всего, перебрав все возможные способы, построим карту раскроя одного стержня (таблица 1).
Таблица 1
Способ |
Количество заготовок А (по 1,5 м) |
Количество заготовок В (по 0,8 м) |
Отходы, м |
1 |
3 |
|
0,5 |
2 |
2 |
2 |
0,4 |
3 |
1 |
4 |
0,3 |
4 |
|
6 |
0,2 |
Для изготовления 20 изделий потребуется 40 заготовок А (202=40) и 60 заготовок В (203=60).
1 Введем переменные.
Обозначим за
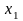 – количество стержней, которые будут
разрезаны I способом,
– количество стержней, которые будут
разрезаны I способом,
 – II способом,
– II способом,
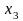 – III способом,
– III способом,
 – IV способом.
– IV способом.
2 Целевая функция Z – отходы. Ее будем минимизировать. Найдем отходы, полученные при разрезании стержней:
 – отходы, полученные
при разрезании
стержней 1-м способом, так как 5 - 3·1,5
= 0,5;
– отходы, полученные
при разрезании
стержней 1-м способом, так как 5 - 3·1,5
= 0,5;
 – отходы, полученные
при разрезании
стержней 2-м способом, так как 5 - 2·1,5
- 2· 0,8 = 0,4;
– отходы, полученные
при разрезании
стержней 2-м способом, так как 5 - 2·1,5
- 2· 0,8 = 0,4;
 – отходы, полученные
при разрезании
стержней 3-м способом, так как 5 - 1·1,5
- 4· 0,8 = 0,3;
– отходы, полученные
при разрезании
стержней 3-м способом, так как 5 - 1·1,5
- 4· 0,8 = 0,3;
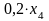 – отходы, полученные
при разрезании
стержней 4-м способом, так как 5–6·
0,8 = 0,2.
– отходы, полученные
при разрезании
стержней 4-м способом, так как 5–6·
0,8 = 0,2.
Тогда
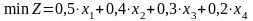 .
.
3 Составим систему ограничений задачи.
1 Ограничение на заготовки А.
При разрезании
стержней 1-м способом получим
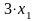 заготовок А,
стержней 2-м способом –
заготовок А,
стержней 2-м способом –
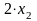 заготовок А,
стержней 3-м способом –
заготовок А, при разрезании
стержней 4-м способом заготовок А не
образуется. Таким образом, всего получим
+
+
заготовок А, что по условию задачи должно
быть не менее 40, т.е.
заготовок А,
стержней 3-м способом –
заготовок А, при разрезании
стержней 4-м способом заготовок А не
образуется. Таким образом, всего получим
+
+
заготовок А, что по условию задачи должно
быть не менее 40, т.е.
 +
+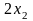 +
+
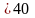 .
.
2 Аналогично получим ограничение на заготовки В:
 .
.
3 Составим ограничения
на смысл переменных. Так как количество
стержней может быть только неотрицательным
числом, то
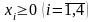 и
и
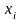 –
целые.
–
целые.
Итак, экономико-математическая модель данной задачи имеет вид
 ;
;

Пример 2
Предприятие за 10 часов должно произвести 31 единицу продукции вида Р1 и 36 единиц продукции вида Р2. Для производства продукции каждого вида может быть использовано оборудование А1 или А2.
Производительность
оборудования этих групп различна и
определяется величиной
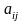 ед./ч, а стоимость 1 часа работы оборудования
составляет
ед./ч, а стоимость 1 часа работы оборудования
составляет
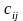 усл. ден. ед./ч
усл. ден. ед./ч
 ,
где i – индекс,
отличающий вид оборудования, а j
– вид продукции. Требуется определить
оптимальный план работы групп оборудования,
на протяжении 10 часов, при котором будет
выполнен план выпуска продукции с
минимальной себестоимостью.
,
где i – индекс,
отличающий вид оборудования, а j
– вид продукции. Требуется определить
оптимальный план работы групп оборудования,
на протяжении 10 часов, при котором будет
выполнен план выпуска продукции с
минимальной себестоимостью.
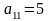 ,
,
 ,
,
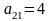 ,
,
 ,
,
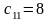 ,
,
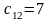 ,
,
 ,
,
 .
.
Решение
Для наглядности составим таблицу 2.
Таблица 2
|
Продукция Р1 |
Продукция Р2 |
|
Оборудование А1 |
ед./ч
|
ед./ч
|
10 ч 10 ч |
Оборудование А2 |
ед./ч
|
ед./ч
|
10 ч |
|
31 ед. |
36 ед. |
|
1 Обозначим за
 – время работы оборудования
– время работы оборудования
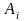 по выпуску продукции
по выпуску продукции
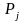
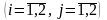 .
.
2 Целевая функция будет
представлять собой затраты на выпуск
продукции, которые необходимо
минимизировать. Так как затраты по
выпуску продукции
 на оборудование
на оборудование
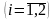 составляют
составляют
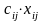 ,
то целевая функция будет иметь вид
,
то целевая функция будет иметь вид
 ,
,
т.е.
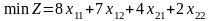 .
.
3 Составим систему ограничений.
1 Ограничение на выпуск продукции Р1.
На оборудовании А1
будет произведено
 единиц продукции Р1.
единиц продукции Р1.
На оборудовании А2
будет произведено
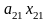 единиц продукции Р1.
единиц продукции Р1.
Таким образом, всего
продукции
 будет произведено
будет произведено
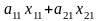 ,
что по условию должно быть равно 31,
получим ограничение
,
что по условию должно быть равно 31,
получим ограничение
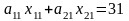 ,
т.е.
,
т.е.
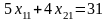 .
.
2 Аналогично получим ограничение по выпуску продукции Р2
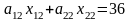 ,
т.е.
,
т.е.
 .
.
3 Ограничение на время работы оборудования А1.
Время работы оборудования А1 по выпуску обоих видов продукции не превышает плановый период 10 ч, следовательно, ограничение будет иметь вид
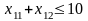 .
.
4 Аналогично получим ограничение на время работы оборудования А2
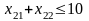 .
.
5 Введем ограничения на смысл переменных, так как время не может быть отрицательным, то
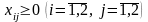 .
.
Таким образом, экономико-математическая модель данной задачи будет иметь вид
 ;
;
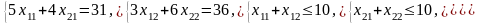
Пример 3
Предприятие может выпускать продукцию двух видов: П1 и П2. Используется три вида ресурсов: оборудование, сырье и электроэнергия. Нормы расхода, запасы ресурсов и прибыль от реализации единицы продукции представлены в таблице 3.
Таблица 3
Ресурсы |
Нормы расхода на единицу продукции |
Запас ресурса |
||
П1 |
П2 |
|||
Оборудование, ч Сырье, кг Электроэнергия, кВт-ч |
2 1 2 |
3 1 1 |
30 12 20 |
|
Прибыль от реализации единицы продукции, ден. ед. |
5 |
4 |
|
|
Найти оптимальный план выпуска продукции.
Решение
Введем переменные:
, – объем выпускаемой продукции П1 и П2 соответственно.
Z – прибыль от реализации всей выпущенной продукции.
Экономико-математическая модель данной задачи будет иметь вид
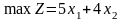 ;
;

Методы решения задач линейного программирования будут рассмотрены ниже.
Пример 6
Решим графически задачу ЛП, экономико-математическая модель которой составлена в примере 3.
;
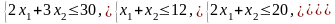 (2.10)
(2.10)
Вначале построим
многоугольник решений или ОДР задачи
(рисунок 1). Для этого в системе координат
 на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
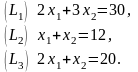
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, например начала координат. Ограничения (2.10) означают, что ОДР лежит в I четверти системы координат . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет многоугольник решений данной задачи (ОДР).
Для того чтобы построить
прямую
 ,
строим направляющий вектор
,
строим направляющий вектор
 ,
который перпендикулярен прямой Z.
Прямая, проходящая через начало координат
и перпендикулярная вектору
,
который перпендикулярен прямой Z.
Прямая, проходящая через начало координат
и перпендикулярная вектору
![]() ,
и будет прямая
,
и будет прямая
![]() .
Затем прямую
перемещаем параллельно самой себе в
направлении вектора N
по многоугольнику решений (ОДР)
(рисунок 1). Последняя точка соприкосновения
прямой
с ОДР и есть оптимальное решение.
.
Затем прямую
перемещаем параллельно самой себе в
направлении вектора N
по многоугольнику решений (ОДР)
(рисунок 1). Последняя точка соприкосновения
прямой
с ОДР и есть оптимальное решение.
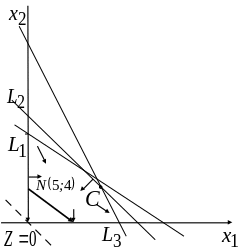
Рисунок 1
Вектор
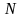 указывает направление возрастания
целевой функции Z.
Оптимальное решение ЗЛП может достигаться
лишь в точках, принадлежащих границе
многоугольника решений. В нашем примере,
как видно из рисунка 1, функция Z
принимает максимальное значение в точке
указывает направление возрастания
целевой функции Z.
Оптимальное решение ЗЛП может достигаться
лишь в точках, принадлежащих границе
многоугольника решений. В нашем примере,
как видно из рисунка 1, функция Z
принимает максимальное значение в точке
 .
Точка
лежит на пересечении прямых
.
Точка
лежит на пересечении прямых
 и
и
 .
Для определения ее координат необходимо
решить систему уравнений:
.
Для определения ее координат необходимо
решить систему уравнений:

Откуда
 .
Это и есть оптимальный план задачи.
Подставив значение
и
в целевую функцию Z,
получаем
.
Это и есть оптимальный план задачи.
Подставив значение
и
в целевую функцию Z,
получаем
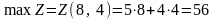 .
.
Таким образом, для того чтобы получить максимальную прибыль в размере 56 ден. ед., необходимо запланировать выпуск 8 ед. продукции вида П1 и 4 ед. продукции П2.
Вариант 5
Составить экономико-математическую модель задачи линейного программирования:
Имеются путевки в дома о тдыха 3-х видов: на 15, 27 и 45 дней. Стоимость их 21 руб., 40 руб. и 60 руб. соответственно.
Сколько и каких путевок надо купить, чтобы потратить не более 2000 руб. и сделать число дней отдыха наибольшим, если общее количество купленных путевок не должно быть более 38.
Решение:
xi – количество путевок на 15, 27 и 45 дней соответственно.
max Z 15x1 27x2 45x3 ;
21x1 40x2 60x3 2000,x1 x2 x3 38,
xi 0,
i 1,3,
xi целые, i 1,3.
Вариант 6
В Пример 8
В трех хранилищах
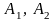 и
и
 имеется соответственно 70, 90 и 50 т топлива.
Требуется спланировать перевозку
топлива четырем потребителям
имеется соответственно 70, 90 и 50 т топлива.
Требуется спланировать перевозку
топлива четырем потребителям
 и
и
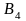 ,
спрос которых равен соответственно 50,
70, 40 и 40 т так, чтобы затраты на
транспортировку были минимальными.
Стоимость перевозки 1 т (в усл. ден. ед.)
указана в таблице 15.
,
спрос которых равен соответственно 50,
70, 40 и 40 т так, чтобы затраты на
транспортировку были минимальными.
Стоимость перевозки 1 т (в усл. ден. ед.)
указана в таблице 15.
Таблица 15
Хранилища |
Потребители |
Запас топлива, т |
|||
В1 |
В2 |
В3 |
В4 |
||
А1 |
5 |
4 |
3 |
6 |
70 |
А2 |
4 |
3 |
5 |
1 |
90 |
А3 |
2 |
4 |
1 |
5 |
50 |
Потребность в топливе, т |
50 |
70 |
40 |
40 |
200\210 |
Решение
Поскольку запасы топлива
в хранилищах превышают спрос потребителей,
введем фиктивного потребителя
 ,
спрос которого равен
,
спрос которого равен
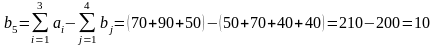
Все
тарифы фиктивного потребителя равны
нулю, т.е.
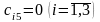 .
После введения фиктивного потребителя
открытая модель задачи преобразовалась
в закрытую, а распределительная таблица
примет вид (см. таблицу 16).
.
После введения фиктивного потребителя
открытая модель задачи преобразовалась
в закрытую, а распределительная таблица
примет вид (см. таблицу 16).
Таблица 16
Хранилища |
Потребители |
Запас топлива, т |
|||||
В1 |
В2 |
В3 |
В4 |
В5 |
|||
А1 |
5 |
4 |
3 |
6 |
0 |
70 |
|
А2 |
4 |
3 |
5 |
1 |
0 |
90 |
|
А3 |
2 |
4 |
1 |
5 |
0 |
50 |
|
Потребность в топливе, т |
50 |
70 |
40 |
40 |
10 |
210 |
|
Найдем начальный опорный
план методом «северо-западного угла.
Сущность его состоит в следующем:
пользуясь распределительной таблицей
закрытой модели, будем распределять
груз, начиная с максимально возможной
загрузки левой верхней, условно называемой
северо-западной клетки, т.е. клетки (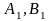 ).
В эту клетку занесем меньшее из чисел
).
В эту клетку занесем меньшее из чисел
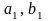 ,
т.е.
,
т.е.
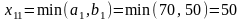 .
Таким образом, потребности в топливе
потребителя
.
Таким образом, потребности в топливе
потребителя
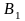 удовлетворены, и первый столбец из
рассмотрения исключается (вычеркивается),
а в хранилище
удовлетворены, и первый столбец из
рассмотрения исключается (вычеркивается),
а в хранилище
 осталось
осталось
 т топлива. Теперь левой верхней клеткой
оставшейся части таблицы является
клетка (
т топлива. Теперь левой верхней клеткой
оставшейся части таблицы является
клетка (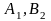 )
и
)
и
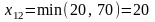 .
Так как в первом хранилище топлива
больше нет, то первая строка из рассмотрения
исключается (вычеркивается), а потребителю
.
Так как в первом хранилище топлива
больше нет, то первая строка из рассмотрения
исключается (вычеркивается), а потребителю
 недостает
недостает
 т топлива. Теперь заполним клетку (
т топлива. Теперь заполним клетку ( )
и
)
и
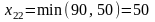 .
Столбец
вычеркиваем, а в хранилище
.
Столбец
вычеркиваем, а в хранилище
 осталось
осталось
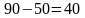 т
топлива. Теперь заполним клетку (
т
топлива. Теперь заполним клетку ( )
и
)
и
 .
Строку
и столбец
.
Строку
и столбец
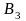 вычеркиваем. Теперь заполним клетку
(
вычеркиваем. Теперь заполним клетку
( )
и
)
и
 .
Столбец
вычеркиваем, а в хранилище
осталось
.
Столбец
вычеркиваем, а в хранилище
осталось
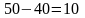 т топлива. Незаполненной осталась одна
клетка (
т топлива. Незаполненной осталась одна
клетка (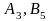 )
и
)
и
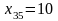 .
Итак в распределительной таблице записан
исходный опорный план (см. таблицу 17).
.
Итак в распределительной таблице записан
исходный опорный план (см. таблицу 17).
Таблица 17
Храни лища |
Потребители |
Запас топлива, т |
|||||
|
В1 |
В2 |
В3 |
В4 |
В5 |
|
|
А1 |
|
|
|
|
|
70 |
|
А2 |
|
|
|
|
|
90 |
|
А3 |
|
|
|
|
|
50 |
|
Потребность в топливе, т |
50 |
70 |
40 |
40 |
10 |
210 |
|
или
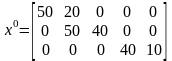 .
.
Транспортные издержки для этого плана:
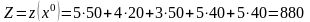 (усл. ден. ед.)
(усл. ден. ед.)
Найдем начальный опорный план методом минимального элемента. Будем распределять груз, начиная с загрузки клетки с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен.
Итак, просматривая
распределительную таблицу, замечаем,
что наименьшие затраты на перевозку
топлива соответствуют маршруту из
хранилища
 потребителю
,
поэтому заполним любую клетку столбца
,
например клетку (
потребителю
,
поэтому заполним любую клетку столбца
,
например клетку (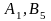 )
и
)
и
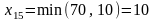 .
Таким образом, потребности в топливе
потребителя
удовлетворены и пятый столбец из
рассмотрения исключается (вычеркивается),
а в хранилище
осталось
.
Таким образом, потребности в топливе
потребителя
удовлетворены и пятый столбец из
рассмотрения исключается (вычеркивается),
а в хранилище
осталось
 т топлива. Просматриваем оставшиеся
клетки таблицы. Наименьшие тарифы имеют
клетки (
т топлива. Просматриваем оставшиеся
клетки таблицы. Наименьшие тарифы имеют
клетки (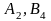 )
и (
)
и ( ):
):
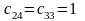 .
Заполняем любую из этих клеток, например
клетку (
)
и
.
Заполняем любую из этих клеток, например
клетку (
)
и
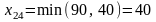 .
Столбец
вычеркиваем, а в хранилище
при этом останется
.
Столбец
вычеркиваем, а в хранилище
при этом останется
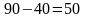 т топлива. Просматриваем оставшиеся
клетки таблицы. Наименьший тариф имеет
клетка (
).
Загрузим ее:
т топлива. Просматриваем оставшиеся
клетки таблицы. Наименьший тариф имеет
клетка (
).
Загрузим ее:
 и вычеркиваем столбец
,
а в хранилище
осталось
т топлива. Просматриваем оставшиеся
клетки таблицы. Наименьший тариф имеет
клетка (
и вычеркиваем столбец
,
а в хранилище
осталось
т топлива. Просматриваем оставшиеся
клетки таблицы. Наименьший тариф имеет
клетка ( ):
):
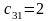 .
В клетку (
)
помещаем
.
В клетку (
)
помещаем
 и вычеркиваем строку
,
а потребителю
недостает
и вычеркиваем строку
,
а потребителю
недостает
 т топлива. Далее по величине тарифа
следует загружать клетку (
),
так как
т топлива. Далее по величине тарифа
следует загружать клетку (
),
так как
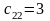 .
В клетку (
)
помещаем
.
В клетку (
)
помещаем
 и вычеркиваем строку
,
а потребителю
недостает
т топлива. Далее по величине тарифа
следует загружать клетку (
),
так как
и вычеркиваем строку
,
а потребителю
недостает
т топлива. Далее по величине тарифа
следует загружать клетку (
),
так как
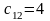 .
В клетку (
)
помещаем
.
В клетку (
)
помещаем
 и вычеркиваем столбец
,
а в хранилище
осталось
и вычеркиваем столбец
,
а в хранилище
осталось
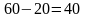 т топлива. Заполняем оставшуюся клетку
(
):
т топлива. Заполняем оставшуюся клетку
(
):
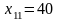 .
Итак, в распределительной таблице
записан исходный опорный план (см.
таблицу 18).
.
Итак, в распределительной таблице
записан исходный опорный план (см.
таблицу 18).
Таблица 18
Хранилища |
Потребители |
Запас топлива, т |
|||||
|
В1 |
В2 |
В3 |
В4 |
В5 |
|
|
А1 |
|
|
|
|
|
70 |
|
А2 |
|
|
|
|
|
90 |
|
А3 |
|
|
|
|
|
50 |
|
Потребность в топливе, т |
50 |
70 |
40 |
40 |
10 |
210 |
|
или
 .
.
Транспортные издержки для этого плана:
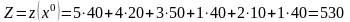
(усл. ден. ед.)
Если в найденном исходном опорном плане число занятых клеток меньше, чем m + n – 1, то найденный опорный план вырожден. Для преодоления вырожденности плана следует добавить «0» в пустую клетку таким образом, чтобы эта клетка не образовывала цикла с занятыми клетками, и считать ее занятой.
Так, в последнем примере
начальный опорный план, найденный
методом северо-западного угла, является
вырожденным (6 занятых клеток, что меньше,
чем
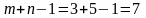 ).
Для преодоления вырожденности этого
плана добавим 0, например, в клетку (
).
Тогда число занятых клеток будет равно
7, и план становится невырожденным.
Клетка (
)
не образует цикла с остальными занятыми
клетками.
).
Для преодоления вырожденности этого
плана добавим 0, например, в клетку (
).
Тогда число занятых клеток будет равно
7, и план становится невырожденным.
Клетка (
)
не образует цикла с остальными занятыми
клетками.
вариант 7
Для
увеличения объемов выпуска пользующейся
повышенным спросом продукции трем
предприятиям выделены капиталовложения
в размере 700 млн. руб. Каждому из предприятий
может быть выделено капиталовложений
в размере 0, 100, 200, 300, 400, 500, 600, 700 млн. руб.
При этом прирост выпуска продукции
каждым из предприятий
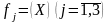 в зависимости от капиталовложений
известно и приведено в таблице.
в зависимости от капиталовложений
известно и приведено в таблице.
Объем
капиталовложений
|
Прирост
выпуска продукции
|
||
Предприятие 1 |
Предприятие 2 |
Предприятие 3 |
|
0 |
0 |
0 |
0 |
100 |
30 |
50 |
40 |
200 |
50 |
80 |
50 |
300 |
90 |
90 |
110 |
400 |
110 |
150 |
120 |
500 |
170 |
190 |
180 |
600 |
180 |
210 |
220 |
700 |
210 |
220 |
240 |
Найти распределение капиталовложений между предприятиями, обеспечивающее максимальное увеличение выпуска продукции.
Решение
Сначала
поставленную задачу нужно рассмотреть
как многошаговую. Будем рассматривать
эффективность вложения средств на одном
(например, первом предприятии), на двух
предприятиях (первое и второе) и, наконец,
на трех предприятиях вместе. Если
![]() млн.
руб. – это капиталовложения в j-ое
предприятие (j = 1,2,3),
то задача состоит в определении
наибольшего значения функции
млн.
руб. – это капиталовложения в j-ое
предприятие (j = 1,2,3),
то задача состоит в определении
наибольшего значения функции
![]() при
условии
при
условии
![]() .
Рекуррентное
соотношение Беллмана в нашем случае
приводит к следующим функциональным
уравнениям:
.
Рекуррентное
соотношение Беллмана в нашем случае
приводит к следующим функциональным
уравнениям:
![]()
![]()
![]() Здесь
функция
Здесь
функция
![]() определяет
максимальный прирост выпуска продукции
при выделении X
млн. рублей капиталовложений первому
предприятию.
определяет
максимальный прирост выпуска продукции
при выделении X
млн. рублей капиталовложений первому
предприятию.
![]() определяет
максимальный выпуск продукции при
распределении X
млн. рублей между первым и вторым
предприятиями.
определяет
максимальный выпуск продукции при
распределении X
млн. рублей между первым и вторым
предприятиями.
![]() –
максимальный прирост при выделении
всем трем предприятиям
–
максимальный прирост при выделении
всем трем предприятиям
![]() млн.
рублей.
1-й
шаг.
Находим по формуле (4.2).
Пусть
млн.
рублей.
1-й
шаг.
Находим по формуле (4.2).
Пусть
![]() ,
тогда
,
тогда
![]()
![]() .
При
.
При
![]() ,
,
![]()
![]() .
При
.
При
![]() ,
,
![]()
![]() .
При
.
При
![]() ,
,
 При
При
![]() ,
,
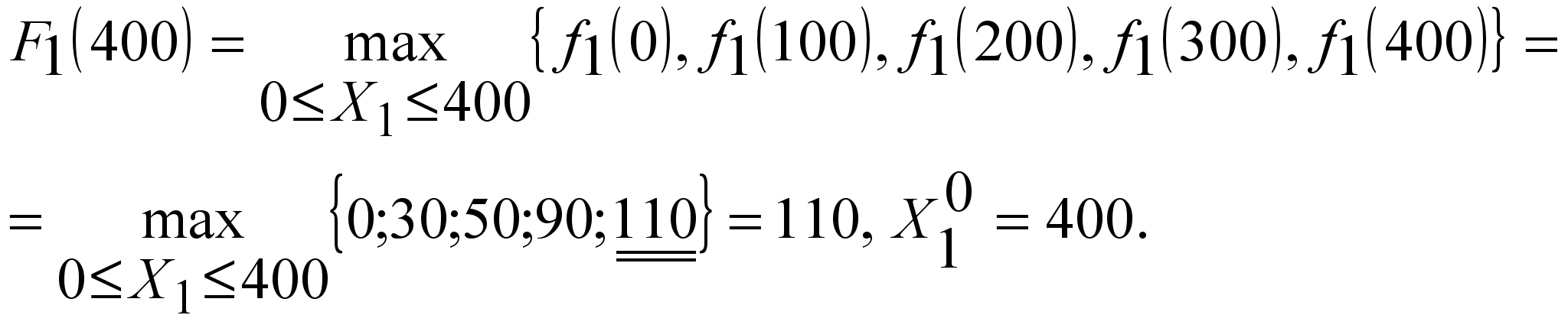 При
При
![]() ,
,
 При
При
![]() ,
,
 При
,
При
,
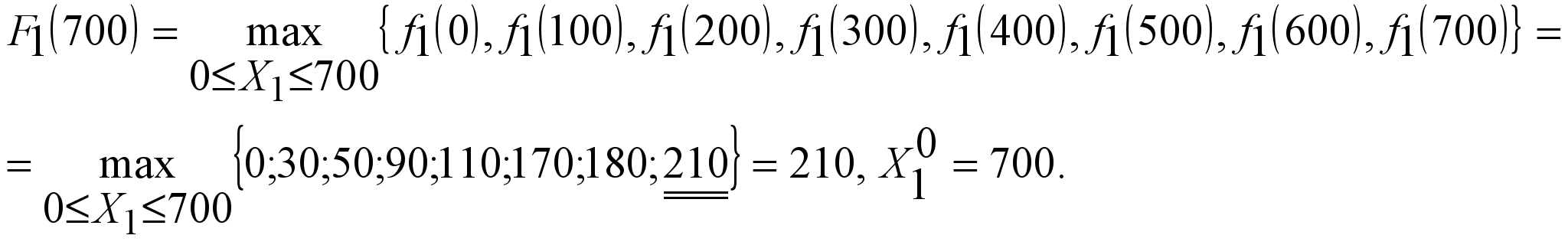 Результаты
вычислений и полученные соответствующие
условно оптимальные значения
Результаты
вычислений и полученные соответствующие
условно оптимальные значения
![]() запишем
в виде таблицы
запишем
в виде таблицы
Объем капиталовложений X, выделяемых первому предприятию, млн. руб. |
Максимальный прирост
|
Условно оптимальный
объем капиталовложений
|
0 |
0 |
0 |
100 |
30 |
100 |
200 |
50 |
200 |
300 |
90 |
300 |
400 |
110 |
400 |
500 |
170 |
500 |
600 |
180 |
600 |
700 |
210 |
700 |
Вариант 8
Найти оптимальную стратегию замены оборудования возраста 3 года на период продолжительностью 10 лет, если для каждого года планового периода известны стоимость
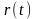 продукции, производимой с использованием
этого оборудования, и эксплутационные
расходы
продукции, производимой с использованием
этого оборудования, и эксплутационные
расходы
 (таблица 24). Известны также остаточная
стоимость, не зависящая от возраста
оборудования и составляющая 4 ден. ед.,
и стоимость нового оборудования, равная
18 ден. ед., не меняющаяся в плановом
периоде.
(таблица 24). Известны также остаточная
стоимость, не зависящая от возраста
оборудования и составляющая 4 ден. ед.,
и стоимость нового оборудования, равная
18 ден. ед., не меняющаяся в плановом
периоде.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
31 |
30 |
28 |
28 |
27 |
26 |
26 |
25 |
24 |
24 |
23 |
|
8 |
9 |
9 |
10 |
10 |
10 |
11 |
12 |
14 |
16 |
18 |
Решение

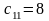 усл.
ден. ед./ч
усл.
ден. ед./ч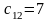 усл.
ден. ед./ч
усл.
ден. ед./ч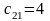 усл.
ден. ед./ч
усл.
ден. ед./ч усл.
ден. ед./ч
усл.
ден. ед./ч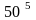
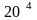
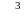
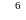


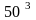

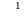
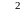

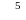
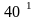
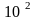
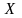 (млн.
руб.)
(млн.
руб.) (млн.
руб.) в зависимости от объема
капиталовложений
(млн.
руб.) в зависимости от объема
капиталовложений выпуска продукции, млн. руб.
выпуска продукции, млн. руб. ,
выделяемый первому предприятию, млн.
руб.
,
выделяемый первому предприятию, млн.
руб.