4.Характер движения потоков.Критерий Рейнольдса.

Физический смысл числа Рейнольдса заключается в  смене режимов течения жидкости. В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые - ламинарный. Турбулентные потоки возникают при высоких скоростях движения жидкости и малой вязкости, ламинарные потоки возникают в условиях медленного течения и в вязких жидкостях. На практике в различных газопроводах, водопроводах и подобных им системах чаще встречаются турбулентные потоки даже при скоростях менее 1м/c. В гидросистемах технологического оборудования, в которых в качестве рабочих жидкостей используются минеральные масла, турбулентный режим возникает при скоростях более 15м/c, тогда как при проектировании таких систем чаще всего предусматривают скорости 4-5м/c. Режим движения в таких трубопроводах, как правило, ламинарный.

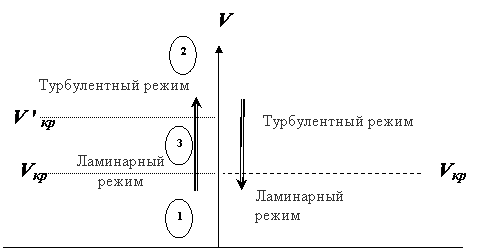
Так как силы инерции и силы вязкости в потоке жидкости зависят от многих причин, то при скоростях, близких к критической, могут возникать переходные режимы, при которых наблюдаются неустойчивое ламинарное или турбулентное движение. Эти режимы отражены на схеме.

Если скорость потока увеличивать, то ламинарный режим (зоны 1 и 3)

переходит в турбулентный (зона 2) при скорости V2кр  –  верхняя критическая скорость. Ей соответствует верхнее число Рейнольдса. Если скорость уменьшать, то переход из турбулентного потока в ламинарный происходит при скорости Vкр- нижняя критическая скорость. Ей соответствует нижнее число Рейнольдса. Зону 3 называют неустойчивой, или переходной, зоной. При скоростях, которые к ней относятся, могут существовать как ламинарные, так и турбулентные потоки. Однако ламинарный режим в этой зоне весьма неустойчив и любое возмущение, например, колебание трубы, моментально приводит к возникновению турбулентного потока. По этой причине на практике эту зону всегда относят к турбулентной, а  под критерием Рейнольдса понимают нижнее число Reкр. В зонах же 1 и 2 режимы движения всегда устойчивы. Даже если режим движения в зоне 1 принудительно изменить, например, с помощью специальных устройств – турбулезаторов потока, то через очень короткое время поток снова станет ламинарным.

5.Потери напора движущегося потока.

Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения^[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).

Гидравлические потери принято разделять на два вида:

• потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;

• местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.

Гидравлические потери выражают либо в потерях напора   в линейных единицах столба среды, либо в единицах давления  :  , где   — плотностьсреды, g — ускорение свободного падения.

Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости^[3] через элемент гидравлической системы пропорциональны квадратускорости жидкости^[2]. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ^[4], которая называется коэффициент потерь иликоэффициент местного сопротивления и такова, что

То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/e_торм, где e_торм = ρw²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость^[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.

Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха^[2]

,

где L - длина элемента, d - характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления

;

таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζ_тр=λL/d.