Тема 4. Элементы аналитической геометрии.

В1. Уравнение прямой на плоскости (параметрическое с угловым коэффициентом, общее, в отрезках, проходящее через две точки). Угол между прямыми. Условия параллельности и перпендикулярности прямых.

Уравнение с угловым коэффициентом:

у=kx+b , k=tgα (k – угловой коэффициент) Если в полученном уравнении b=0, то y=kx, прямая проходит через начало координат. Если k=0, то прямая || Оу.

Общее ур-е прямой:

Ax+By+C=0, где А, В, С – произвольные сила, при чем А≠В одновременно. Ели А=0 – прямая || Ox. Если В=0, то прямая || Оу. Если С=0, то прямая проходит через начало координат.

Ур-е прямой в отезках:

Уравнение прямой, проходящей через 2 данные точки:

Если , то ур-е || Oy. Если , то || Ох.

Если уравнения прямой заданы в общем виде

A₁x + B₁y + C₁ = 0,         

A₂x + B₂y + C₂ = 0,     (6)

угол между ними определяется по формуле

     (7)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

     (10)

В2. Прямая в пространстве (каноническое, как линия пересечения плоскостей, параметрическое уравнение прямой).

Каноническое:

Как линия пересечения двух плоскостей

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

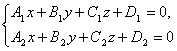
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Параметрическое уравнение прямой:

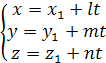
В3. Плоскость (общее уравнение, уравнение плоскости в отрезках, частные виды плоскостей).

Общее уравнение плоскости:

Ax+By+Cz+D=0 .

Уравнение плоскости в отрезках:

Частные виды плоскостей:

1) By + Cz + D = 0 (A=0) - параллельна оси Ox;

2) Ax + Cz + D = 0 (В=0) - параллельна оси Oy;

3) Ax + By + D = 0 (C=0) - параллельна оси Oz;

4) Cz + D = 0 (А=В=0) - параллельна оси Oxy;

5) By + D = 0 (А=С=0) - параллельна оси Oxz;

6) Ax + D = 0 (В=С=0) - параллельна оси Oyz;

7) Ax + By + Cz = 0 (D=0) - проходит через начало координат;  

8) By + Cz = 0 (A=D=0) - проходит через ось Ox;

9) Ax + Cz = 0 (B=D=0) - проходит через ось Oy;

10) Ax + By = 0 (C=D=0) - проходит через ось Oz;

11) z = 0 - плоскость Oxy;

12) y = 0 - плоскость Oxz;

13) x = 0 - плоскость Oyz.