В1. Линейная комбинация векторов. Понятие линейной зависимости векторов. Свойства линейной зависимости векторов.

Пусть каждый из векторов x, a₁,a₂,..,a_n — есть n-мерный вектор. Вектор x называется линейной комбинацией векторов a_1, a₂, a_n, если найдутся такие действительные числа £₁, £₂, £_m, не все одновременно равные нулю, что x=£₁a₁+£₂ a₂+..+£_ma_n(1), при этом если хотя бы один из коэффициентов отличен от нуля, то такая система называется линейно зависимой. Если равенство (1), возможно только при £₁=£₂=…=£_m=0, то такая система называется линейно независимой.

Свойства линейной зависимости векторов:

1. Если среди набора векторов один из них есть линейная комбинация части остальных, то весь набор векторов линейно зависим.

2. Если среди наборов векторов имеется нулевой вектор, то этот набор линейно зависим.

3. Если в системе векторов имеется два равных вектора, то она линейно зависима.

4. Если в системе векторов имеется два пропорциональных вектора, то она линейно зависима.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов a_1, a₂, a_n линейно независима, а после присоединения к ней вектора a оказывается линейно зависимой, то вектор “а” можно разложить по векторам a_1, a₂, a_n, и при том единственным образом, т.е. коэффициенты разложения находятся однозначно.

В2. Базис и размерность векторного пространства.

Векторное пространство   называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным. Совокупность n линейно независимых векторов n- мерного векторного пространства   называется его базисом.

Теорема 1. Каждый вектор   линейного n- мерного пространства   можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

Теорема 2. Если   - линейно независимые векторы пространства   и любой вектор   линейно выражается через  , то эти векторы образуют базис в  .

В3. Теорема о разложении любого вектора по векторам базиса. Каждый вектор   линейного n- мерного пространства   можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

Доказательство. Пусть   - произвольный базис пространства   и  . Так как любые n+1 векторов пространства   линейно зависимы, то зависимы, в частности, и векторы  , т.е. существуют не равные одновременно нулю числа  , такие, что

.

При этом  , в противном случае хотя бы одно из чисел   было бы отлично от нуля, и вектора   были бы линейно зависимы. Следовательно,

.

Полагая  , будем иметь  .

Это представление   через   единственно. Доказывается от противного. Числа   называются координатами вектора   в базисе  .

В4. Связь координат вектора в различных базисах одного и того же пространства. Свойства матрицы переходов.

Пусть в линейном пространстве заданы два базиса:

e = (e₁, e₂, …, e_n) (назовём его старым базисом) и

= (e₁', e₂', …, e_n') (назовём его новым базисом).

Разложим векторы базиса e^' по базису e:

(1)

Матрицу Т=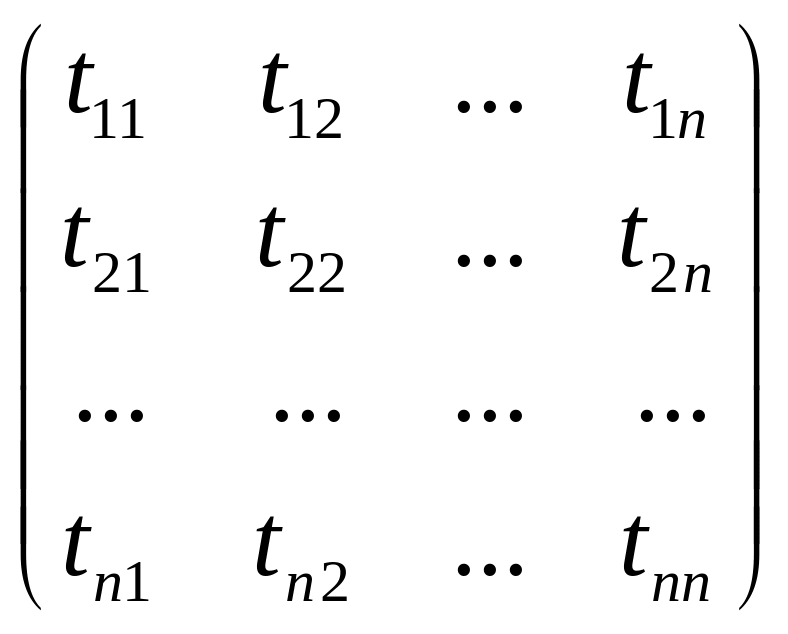 называют матрицей перехода от базиса e к базису . Равенства (1) в матричном виде удобно записывать так: =е·Т (2).

Умножение символической матрицы-строки   на матрицу перехода T в (2) производится по правилам умножения матриц.

Пусть в базисе   вектор   имеет координаты  , а в базисе   — координаты  , т.е.

Подставляя в правую часть последнего равенства выражение (2), получаем 

v = (e) υ =(e)Tυʹ — два разложения вектора   в одном и том же базисе  . Коэффициенты этих разложений должны совпадать, так как это координаты одного и того же вектора в одном базисе. Поэтому

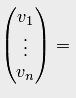
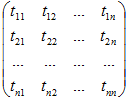
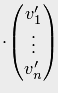(3)

Формула (3) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.

Свойства матрицы перехода:

• Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.

• 

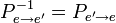
В5. Скалярное произведение.

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

ᾱ b= ᾱ *b=( ᾱ,b)=│ᾱ││b│cos(ᾱ^,b)

В6. Евклидово пространство. Матрица Грамма. Процесс ортогонализации.

Вещественное линейное пространство L называется евклидовым, если в нём определена операция скалярного умножения: любым двум элементам x, yL сопоставлено вещественное число a = (x, y) , удовлетворяющее следующим требованиям, каковы бы ни были элементы x, y, zÎL и число aÎR:

1. (x, y)= (y, x) ;

2. (x + y, z) = ((x, z) + (y, z));

3. (ax, y)= (x,ay)= a(x, y) ;

4. (x, x)> 0 для всех x ¹ q ;

5. (x, x)= 0 , если x = q .

Любое подпространство L¢ Í L - также является евклидовым пространством, так как для его элементов определено то же самое скалярное умножение.

В7. Свойства длин и расстояний в Евклидовом пространстве

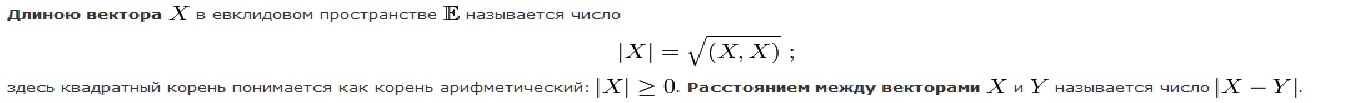
В8. Квадратичные формы. Канонический вид. Метод Лагранжа. Закон инерции.

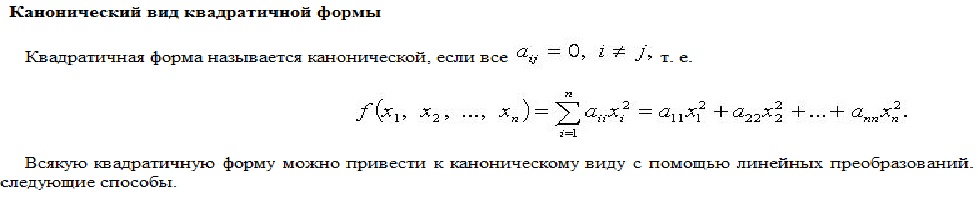
В9. Положительно(отрицательно) определённая квадратичная форма. Критерий Сильвестера.

В10. Определение линейного оператора.

Пусть Rⁿ и R^m лин. пространства размерности n и m. Отображением лин. пр-ва Rⁿ в лин-е пр-во R^m наз-ся правило : каждому Х Rⁿ ставится в соотв. единственный эл-т у R^m ; У = (х). Частным случаем отображения является ф-я у= f(х).

Эл-т прост-ва- не обязательно вектор, это м.б. скалярный элемент, м-ца и т.д. Отображение линейное, если для любого элемента Х и любого числа вып-ся соотношения:

1) (х₁ + х₂) = (х₁) + (х₂); 2) Р ( х) = (х).

Будем рассматривать лин. отображения, действующие из векторного пр-ва Rⁿ в это же пр-во Rⁿ. Подобные отображения - линейные операторы.

Действия над линейными операторами.

Введем арифметические операции с лин. операторами:

1) ₁ + ₂ = –оператор, действ-й по след. правилу: ₁(х) + ₂(х).

2) ₁ * = – оператор, действ-й по правилу: (х)= * ₁(х).

3) _{2 * 1} = – оператор, определяемый из равенства: = ₂ ( ₁(х)).

Оператор тождественный или единичный, если (х) = х.

Все введенные операторы – линейные.

Докажем, что оператор произведения линеен, т.е. ₂ ( ₁( *х + µ*у)) = ₂ ( ₁(µу)), = Р₂ ( * ₁(х)+ µ* ₁(у))

= * ₂ (Р₁(х)) + µ* ₂ ( ₁(у))= * (х) + µ * (у) – что подтверждает линейность данного оператора.

Матрица оператора в разных базисах.

Теорема( О связи матриц оператора в разных базисах).

Пусть Р и P` м-цы лин-го оператора в старом и новом базисе.

Р= (е₁, e₂,…e_n), P` =(е<sub>1</sub>`, e₂`,…e<sub>n</sub>`).

Р`= T^-1*P*T, где Т- м-ца перехода от старого базиса к новому.

Док-во: Пусть в пр-ве Rⁿ заданы базисы е₁, e₂,…e_n и е₁`, e<sub>2</sub>`,…e_n`, воздействие оператора х порождает вектор у. У=Р*Х в старом базисе и У`=P`* X` в новом базисе.

Пусть Т- м-ца перехода от старого базиса к новому, тогда Х=Т*Х`;У= Т*У`; умножив рав-во Х=Т*Х` на м-цу Р слева : РХ= РТХ`; У=РТХ`; ТУ`=РТХ`. Умножим слева на Т<sup>-1</sup>: Т<sup>-1</sup> *ТУ`= Т^-1*Р*Т*Х`. У`= Т^-1 * Р*Т*Х`. сравнивая с У`=P`*X`, отсюда Р`= Т^-1 *РТ.

Теорема( Об определителе оператора в разных базисах).

Определитель м-цы лин-го оператора не зависит от выбора базиса.

Док-во: Вычислим опр-ль Р`= Т^-1 *РТ, исп-я св-ва опр-ля произведения матриц :

|Р`|=| Т^-1 *РТ |=| Т^-1 |*|Р|*|Т|=| Т^-1|*|Т|*|Р|=| Т^-1 *Т |*|Р|=|Р|.

Следствие: Ранг м-цы лин-го оператора не зависит от выбора базиса.

Пр: в базисе е₁, e₂, e₃; Р= . Найти м-цу оператора в новом базисе е₁`, e<sub>2</sub>`,e₃`, связ-м со страым базисом м-цей перехода. Т= .

Р`= Т^-1 *Р*Т- мы ищем данную м-цу.

обр. м-ца: Т^-1 = . Р`= .=

|Р|=-4+6+6-1=7; |P`|= 120+16*18+27*11-9*18-360-16*11=7,т.о. опр-ль м-цы не изм-ся при переходе к др. базису.