10. Привязочные работы в полигонометрии: постановка задачи и пути ее решения.

Привязка полигонометрии к пунктам государственной геодезической сети производится для определения координат пунктов полигонометрического хода и для передачи направления на стороны хода. Привязку полигонометрии к пунктам геодезической сети можно произвести различными способами в зависимости от расположения этих пунктов по отношению к пунктам полигонометрии.

Для привязки хода необходимо иметь координаты начала и конца хода и дирекционные углы исходных начальной и конечной сторон хода. Самым простым способом привязки является непосредственное примыкание полигонометрического хода к пунктам триангуляции или полигонометрии высшего класса. В этом случае привязка осуществляется измерением примычных углов.

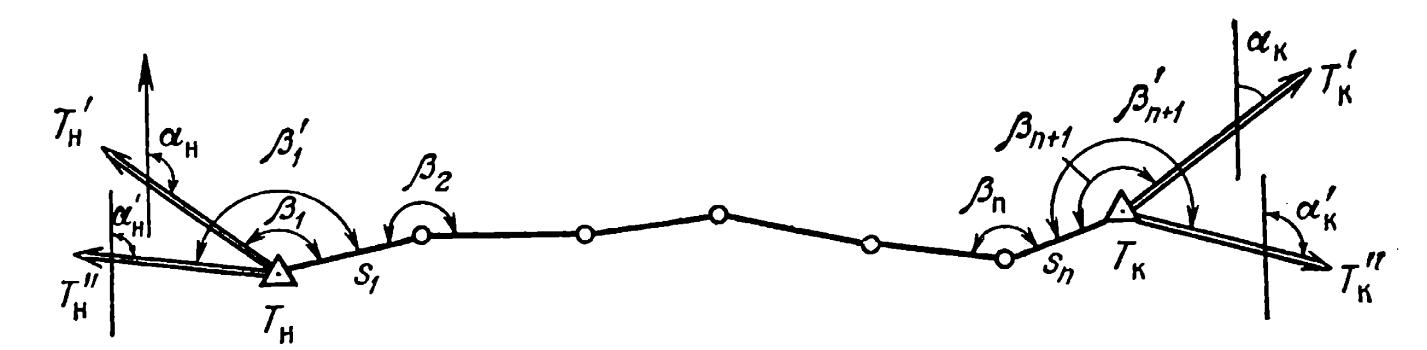
Если известны координаты пунктов Т_Н и Т_К (см. рис.), из которых видны пункты государственной геодезической сети Т’_Н, Т’’_Н, Т’_К, Т’’_К, то на пункте Т_Н необходимо измерить примычные углы β₁ и β’₁, а на пункте Т_К — углы β_n+1 и βэ_n+1. Вычислив по координатам пунктов Т_Н, Т_К, Т’_Н, Т’’_Н, Т’_К, Т’’_К дирекционные углы α_Н, α’_Н, α_K, α’_K сторон Т’_НТ_Н, Т’’_НТ_Н, Т_КТ’_К, Т_КТ’’_К, можно передать дирекционные углы на стороны полигонометрического хода и s_n. Этот способ привязки дает надежный контроль, так как разность примычных углов β₁ и β’₁, β_n+1 и β’_n+1 должна равняться разности дирекционных углов α_Н и α’_Н, α_K и α’_K.

В ряде случаев не удается один из концов хода или оба конца привязать к исходным направлениям. Например, когда на исходном пункте отсутствует видимость g земли на соседние пункты, наружные знаки пришли в ветхость, а центры на ориентирных пунктах потеряны. В таких случаях на этом конце хода осуществляют привязку лишь к пункту, а примычный угол между направлением последней линии хода и исходным направлением остается неизмеренным.

Однако в практике геодезических работ бывают случаи, когда непосредственно привязку полигонометрии к пунктам государственного геодезического обоснования осуществить почему-либо невозможно. Тогда применяют особые способы привязки, которые можно разделить на две группы: 1) привязка к близлежащему пункту; 2) привязка к отдаленному пункту.

Используя различные способы привязки, можно получить также координаты ряда боковых пунктов.

11. Передача координат с вершины знака на землю. Постановка задачи. Чертеж.

11+12+13. Передача координат с вершины знака на землю. Вычисление координат и контроль решения задачи + Оценка точности.

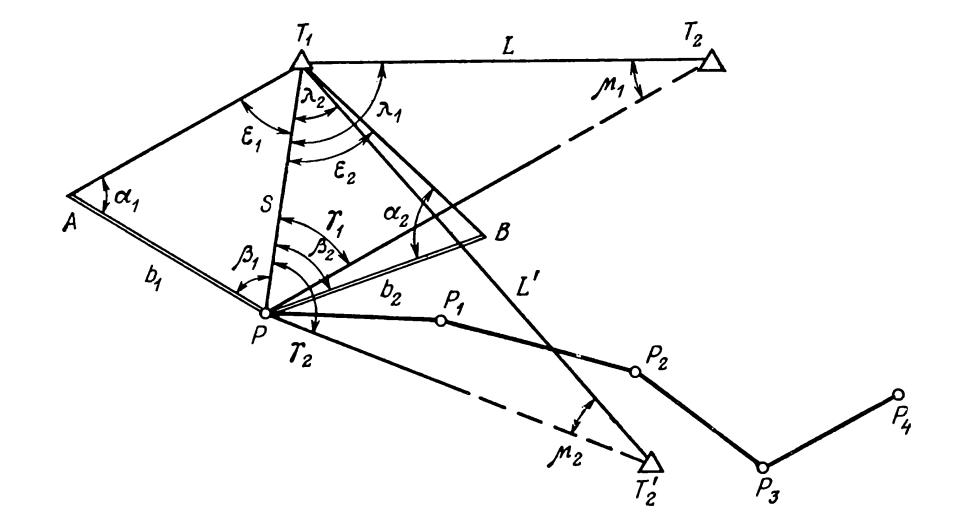рис.1

1. Пункт, к которому производится привязка, недоступен ни для линейных, ни для угловых измерений (обычно это шпиль какого-либо здания).

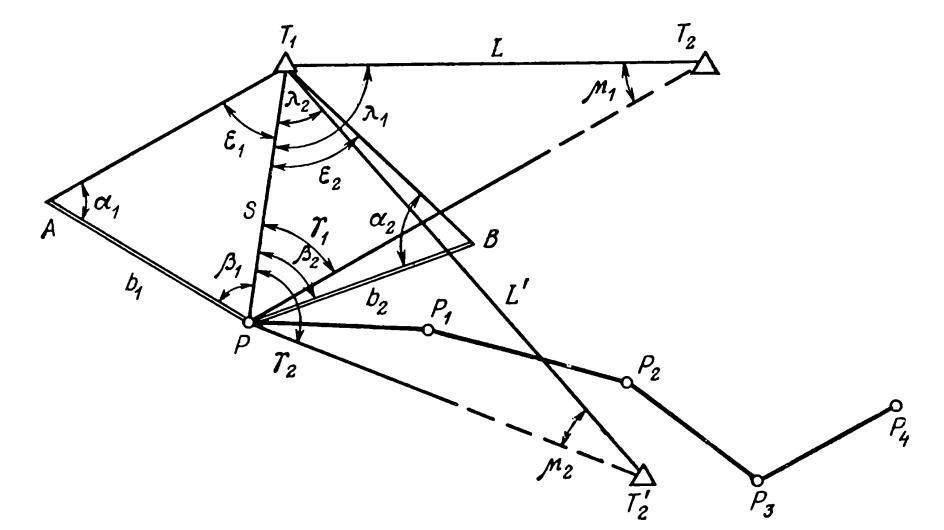
Необходимо определить координаты пункта Р (см. рис.1), из которого видны пункты обоснования: близко расположенный пункт Т₁ и пункт Т₂, последний может быть расположен вдалеке от пункта Р. Более надежный контроль решения задачи будет обеспечен в том случае, если, кроме пункта Т₂ будет виден еще пункт Т’₂.

Расстояние РТ₁=s можно определить как неприступное. Для этого на местности строят два треугольника АРТ₁ и ВРТ₁. Стороны этих треугольников АР (b₁) и ВР (b₂) измеряют непосредственно; кроме этого, в каждом треугольнике измеряют по два угла α₁, β₁, α₂, и β₂.

Из треугольников АРТ₁ и ВРТ₁ определяют длину РТ₁=s по формуле (XV.1), где

(XV.2), а i= 1, 2. Из полученных значений берут среднее.

Для определения примычного угла λ₁ на местности при точке Р измеряют угол γ₁. Этот угол дает возможность определить сначала из треугольника РТ₁Т₂ угол μ₁, а затем и угол λ₁. В треугольнике РТ₁Т₂ дирекционный угол линии (Т₁Т₂)* и ее длину Т₁Т₂= L находят из решения обратной геодезической задачи по формулам:

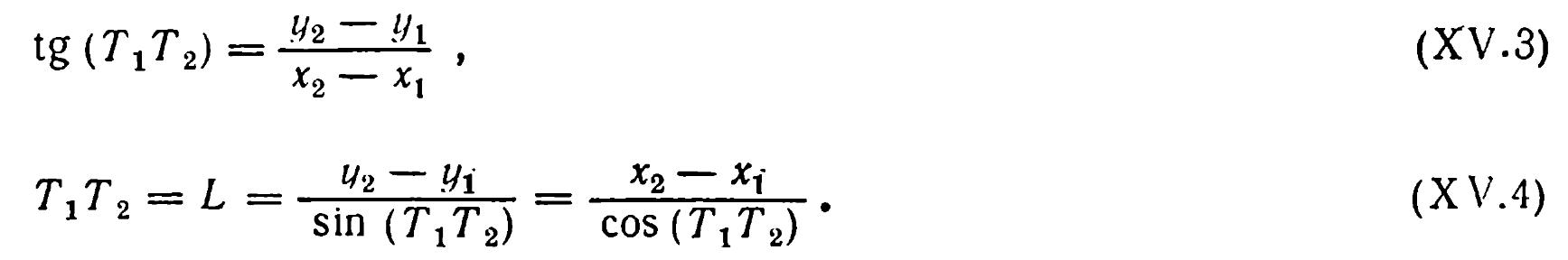
Надежнее контроль обратной геодезической задачи выполнить по формуле:

так как, вычисляя tg (Т₁Т₂) по формуле (XV.3), можно допустить

ошибку в разности ординат (у₂ — у₁) или абсцисс (х₂ — х₁), и эта ошибка при контроле по формулам (XV.4) останется незамеченной, хотя Т₁Т₂ и вычисляют дважды.

Зная величину L, из треугольника РТ₁Т₂ находят sin μ₁= s/L * sin γ₁ (XV.6), а затем по таблицам — угол μ₁.

Примычный угол λ₁ получают из того же треугольника как дополнение до 180°: (XV.7)

Дирекционный угол φ направления Т₁Р определяют как (XV.8)

Выбор знака перед λ₁ в формуле (XV.8) производится с учетом расположения пунктов на схематическом чертеже, составление которого при решении задачи необходимо.

По полученным длине линии РТ₁ и дирекционному углу ее (Т₁Р) находят приращение координат, а затем координаты соответственно по формулам:

(XV.9) и (XV.10).

Заключительный контроль решения задачи состоит в вычислении дирекционного угла (РТ₂) (XV.11) и вторичном получении угла (XV.12)

Если из пункта Р будет виден пункт Т’₂, его необходимо использовать для вторичного получения значения координат пункта Р, для чего следует на пункте Р измерить угол γ₂, а далее повторить решение задачи, начиная с получения tg (Т₁Т’₂) и L’ по формулам (XV.3) и (XV.4) и т.д. до конца.

Оценка точности при решении задачи состоит в получении средних квадратических ошибок вычисленных элементов: линии РТ₁=s дирекционного угла (Т₁Р)=φ и положения пункта Р.

Для проведения оценки точности необходимо иметь показатели точности измерения базисов (m_b — при измерении светодальномером, μ и λ — при измерении инварной проволокой) и углов (m_α, m_β, m_γ).

Для получения m_si возьмем функцию (XV.1), прологарифмируем ее, а затем дифференцированием найдем (XV.13), при этом учтем, что угол ε определяется по формуле (XV.2), следовательно,

Переходя от (XV.13) к средним квадратическим ошибкам и принимая m_αi = m_βi (углы измерены равноточно), найдем (XV.14)

Средняя квадратическая ошибка среднего значения линии s_cp будет (XV.15)

Величинами m_si можно воспользоваться для подсчета предельного расхождения в значениях s_i, вычисленных из двух треугольников, так как

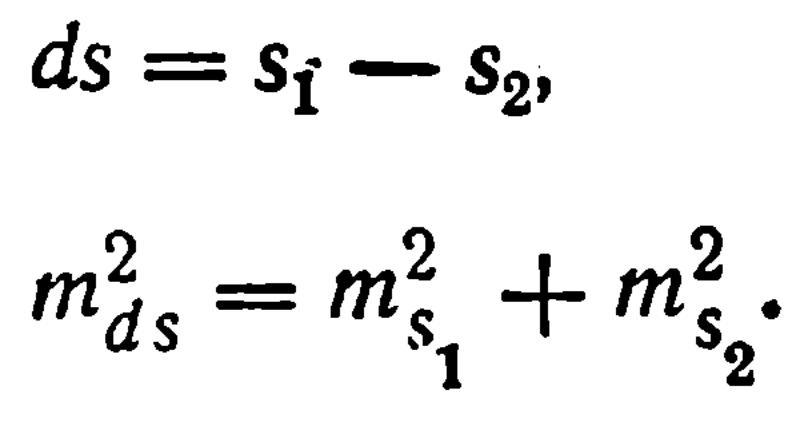
Тогда (XV.16)

Определим среднюю квадратическую ошибку дирекционного

угла φ₁. Дифференцируя формулы (XV.8), получим (XV.17), где i = 1, 2.

Угол λ_i вычисляется по формуле (XV.7), следовательно, дифференцирование ее дает (XV.18).

В свою очередь величина μ_i, определяется выражением (XV.6). Несколько упростим его, имея в виду, что отношение s/L, как правило, равно 1/10. С учетом этого формулу (XV.6) можно написать sin μ_i = 1/10 sin γ_i.

Дифференцируя ее, получим откуда .

Можно считать, что отношение

cos γ_i/cos μ_i < 1.

Тогда

dμ_i ~ 1/10dγ_i.

Учитывая это соотношение, можно в формуле (XV. 18) dμ_i при оценке точности в расчет не принимать и принять

dλ_i ~ dγ_i, или с учетом (XV. 17) dφ_i ~ dγ_i.

Отсюда, переходя к средним квадратическим ошибкам, будем иметь m_φi ~ m_γi (XV.19).

Нетрудно установить, что строгая формула средней квадратической ошибки дирекционного угла будет иметь вид m²_φi = (1 + tg μ_i*ctg γ_i)² m²_γi + ρ² tg² μ_i (m_si/s_i)² (XV.20)/

Средняя квадратическая ошибка среднего значения дирекционного угла φ_ср в случае определения его по двум пунктам T₂ и Т’₂ (c учетом (XV. 19)) будет равна M²_φ=1/2 √2m²_γ = 0,71mγ (XV.21), где m_γ = m_γ1 = m_γ2.

Предельное расхождение между значениями ф, полученными по двум пунктам, определится выражением пред(φ₁ — φ₂) = 2√2m²_γ = 2,8m_γ . (XV.22)

Для получения средней квадратической ошибки положения пункта Р воспользуемся рис. 2. Допустим, что под влиянием ошибок в длине линии ds и в дирекционном угле dφ пункт Р сместился со своего верного положения на величину dp. Это смещение можно разложить на компоненты ds и u, где u=s*dφ/ρ, тогда dP² = ds² + u² или dP² = ds² + s*dφ/ρ (XV.23).

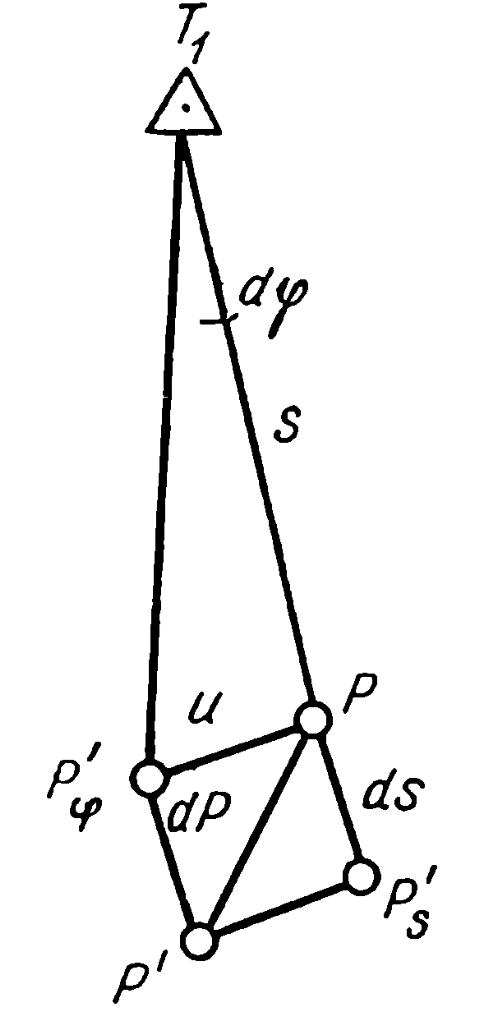Рис.2

Предположим, что определение пункта повторено достаточно большое число раз и что имеется n равенств вида (XV.23). Сложив эти равенства и разделив затем обе части суммарного равенства на число n получим:

(XV.24), где М_φ и M_s — средние квадратические ошибки φ_ср и s_cp.

Анализ формул показывает, что для обеспечения большей точности передачи координат с пункта Т₁ на пункт Р необходимо:

а) строить по возможности равносторонние вспомогательные треугольники APT₁ и ВРТ₁ это обеспечит большую точность вычисления s;

б) выбирать положение пункта Р так, чтобы угол γ был близок к прямому (Т₁Р примерно перпендикулярно к РТ₂), тогда угол μ будет получен с большей точностью.

2. Пункт, к которому производится привязка, доступен для угловых, но не доступен для линейных измерений. Таким пунктом может быть, например, геодезический знак, построенный на крыше какого-либо дома, что часто

имеет место в городах.

В этом случае величина угла λ измеряется и задача сводится к вычислению неприступного расстояния Т₁Р =s, которое определяется из решения двух треугольников APT₁ и ВРТ₁. Углы ε₁ и ε₂ в этих треугольниках измеряются непосредственно.