17. Уклон линии местности. График заложений.
Уклон линии местности – отношение превышения к заложению линии, мера крутизны ската.
Уклоны выражаются в процентах или в промиллях (‰). Чем больше заложение (расстояние между двумя соседними горизонталями на плане), тем меньше крутизна.
График заложений по уклонам, формула: d=h/i (заложение равно превышение на уклон).
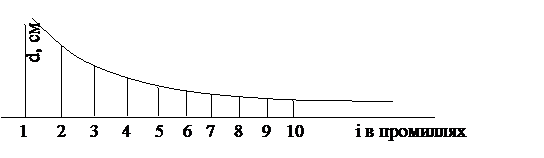
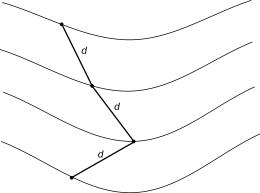
График заложений по углам строится по формуле: d=h/ctg v (заложение на котангенс v, если tg v = I, а h – постоянная для каждой карты).
График заложений используется для построения линий с заданным уклоном. Для этого в раствор циркуля берётся необходимое значение и проводится линия.
18. Определение водосборной площади.
Водосборная площадь – территория, с которой вода атмосферных осадков стекает к данной точке.
Границы в.п. определяются по кратчайшему расстоянию между горизонталями через вершины холмов седловины, по водоразделам.
Граница водосборной площади проходит по линии водораздела, граница этой площади всегда - замкнутая линия.
Для определения границ водосборной площади на карте проводят водораздельные линии, а затем от проектируемого сооружения к водораздельным линиям проводят линии наибольшего ската, перпендикулярные горизонталям.
19. Проектирование линии заданного уклона на карте.
- см. вопрос 17:
(17. Уклон линии местности. График заложений. )
Уклон линии местности – отношение превышения к заложению линии, мера крутизны ската.
Уклоны выражаются в процентах или в промиллях (‰). Чем больше заложение (расстояние между двумя соседними горизонталями на плане), тем меньше крутизна.
График заложений по уклонам, формула: d=h/i (заложение равно превышение на уклон).
График заложений по углам строится по формуле: d=h/ctg v (заложение на котангенс v, если tg v = I, а h – постоянная для каждой карты).
График заложений используется для построения линий с заданным уклоном. Для этого в раствор циркуля берётся необходимое значение и проводится линия.
20. Определение отметок точек на карте.
Абсолютную высоту какой-либо точки местности, отметка которой на карте не подписана, определяют по отметке ближайшей к ней горизонтали.
Для определения высоты точки нужно умножить разницу высот нижележащей и вышележащей горизонтали (высоту сечения рельефа ) на отношение расстояния от ниж. гор. до точки и от точки до выш. гор.
Если точка лежит на горизонтали – её высота равна высоте горизонтали, ели она находится в замкнутой горизонтали – к показателю этой горизонтали добавляется половины высоты сечения рельефа.
21. Геодезические измерения и характеристики их точности.
Измерение – определение физической величины опытным путём, с применением специальных технических средств. Определённую величину сравнивают с единицей меры.
l = q•n, где q – единичное измерение, l – измерение, n – число измерений.
Измерения бывают линейные, угловые, площадные.
1) Линейные измерения отражают длину, расстояние, протяжённость. Обычно в метрах, сантиметрах, километрах, миллиметрах.
2) Угловые меры – градус (1/90 прямого угла), град (1/100 пр. угла) и радианы (360/2П).
3) Площадные – в километрах в квадрате и гектарах.
Под точностью измерений понимается степень близости результата измерения к истинному значению измеряемой величины. Точность результата измерений зависит от условий измерений.
22. Классификация геодезических измерений.
1) Прямые и косвенные (на местности или результат вычисления).
2) Необходимые и избыточные (один результат или сверх необходимого).
3) Равноточные или неравноточные.
Равноточными называются результаты, полученные при определённых условиях:
- инструменты одной точности
- одна квалификация у исполнителей
- одна и та же методика
- одинаковые условия среды.
23. Погрешности геодезических измерений.
Погрешность - оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
- грубые (легко обнаружить, исключаются при повторах)
- случайные (изменяются случайным образом)
- систематические (по знаку и величине одинаковые, однообразно повторяются).
24. Свойства случайных ошибок.
- не превосходит предела «предельной ошибки» (эта граница позволяет избежать грубых ошибок).
- положительные и отрицательные ошибки случаются одинаково часто.
- чем больше абсолютная величина ошибки, тем она реже встречается в ряду.
- при приближении кол-ва измерений к бесконечности, среднее арифметическое ошибки стремится к нулю.
25. Числовые характеристики оценки точности геодезических измерений.
1) Абсолютная (истинная) погрешность.
В тех же единицах, что и результат. Равна разнице истинного значения и результата измерений.
2) Относительная погрешность.
Отношение абсолютной погрешности к результату, или истинному значению. Безразмерная величина.
3) Среднеквадратическая погрешность.
Квадрат среднеквадратической ошибки = среднее арифметическое из квадратов истинных погрешностей. Находится по формуле Гаусса: квадрат суммы квадратов абсолютных погрешностей для каждого измерения, деленный на кол-во измерений.
4) Предельная: плюс/минус среднеквадратическая умноженная на 3.
5) Вес измерения – число, служащее оценкой доверия к тому или иному отдельному результату измерения, входящему в ряд неравноточных измерений. Характеристика точности для неравноточных измерений относительна. Равен коэффициенту пропорциональности деленному на квадрат кол-ва измерений.