Часть 2

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Глава 1

Предел функции

1.1. Предел функции в точке

Пусть функция определена в некоторой окрестности точки , кроме, быть может, самой точки .

Число называется пределом функции при , стремящемся к (записывается ), если для любого сколь угодно малого числа найдется такое чи­сло (вообще говоря, зависящее от ), что для всех таких, что , , выполняется неравенство . Предел функции обозначается так: .

1.2. Предел функции на бесконечности

Пусть функция f(x) определена на бесконечном промежутке . Число А называется пределом функции при x стремящемся к бесконечности (записывается ) если для любого числа  > 0 найдется такое число , что для всех значений имеет место неравенство | f(x) – А| < .

Если число А является пределом функции f(x) при , стремящемся к бесконечности, то пишут .

1.3. Операции над пределами

Пусть функции и определены в некоторой окрестности точ­ки х₀ и имеют пределы , . Перечислим без доказательства свойства пределов от суммы (разности), произведения и частного этих функций.

1. Предел суммы (разности) этих функций равен сумме (разности) их пределов:

2. Предел произведения функций равен произведению их пределов:

.

Отсюда, в частности, вытекает, что постоянный множитель можно выносить за знак предела функции:

3. Предел частного функций равен частному их пределов (при усло­вии в 0):

.

Пример 1.1 =

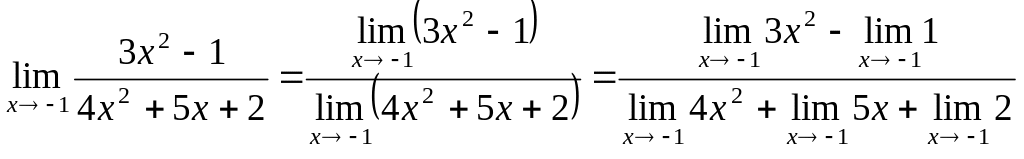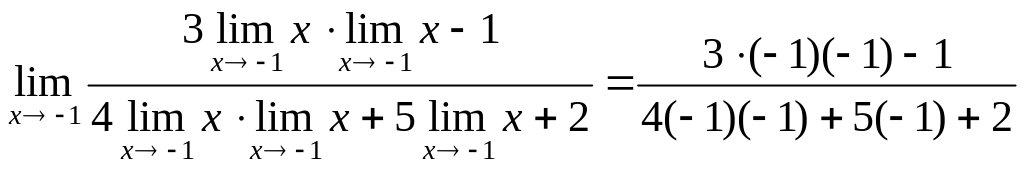= = 2.

Из этого примера следует, что указанный предел может быть найден, если в выражение подставить значение .

Пример 1.2

. Аналогично предыдущему примеру, нетрудно убедиться, что , а =11,

поэтому .

1.4. Бесконечный предел

Пусть функция определена в некоторой окрестности точки , кроме быть может, самой точки x₀.

Говорят, что =  (предел функции равен бесконечности), если для любого сколь угодно большого числа найдется такое чи­сло (вообще говоря, зависящее от М ), что для всех таких, что , , выполняется неравенство .

1.5. Бесконечно малые и бесконечно большие величины

Бесконечно малая. Функция называется бесконечно малой величиной (или просто бесконечно малой) при (или ), если

( или )

Например, – бесконечно малая при , – бесконечно малая при , функция – бесконечно малая при .

Бесконечно малые функции будем обозначать , , , . . . (или просто , , , . . . ).

Бесконечно большая. Функция называется бесконечно большой величиной (или просто бесконечно большой) при (или ), если

( или )

Бесконечно большие функции будем обозначать , , , . . . (или просто , , , . . . ).

В дальнейшем, вместо слов “бесконечно малая” будем иногда писать БМ, а вместо слов “бесконечно большая” – ББ.

Между бесконечно малыми и бесконечно большими существует связь. Если функция – БМ при , то функция – ББ при . И наоборот, если функция является ББ при , то функция – БМ при .

Например, – бесконечно большая при , – бесконечно большая при , а функция – бесконечно большая при .

Другими словами, деление конечной величины на бесконечно малую в результате дает бесконечно большую.

Пример 1.3.

Найдем . Не трудно убедиться, что числитель этой дроби стремится к 11, а знаменатель стремится к 0 (см. пример 1.2), поэтому = = .

Здесь (и в дальнейшем) запись в квадратных скобках означает, что знаменатель этой дроби не равен 0, а только стремится к этому значению (соответственно и числитель не равен, а только стремится к 11).