Двухцилиндровый V-образный двигатель с общим кривошипом
Наиболее распространенной является
схема с углом между осями цилиндров
.
Для этого случая в соответствии с
принятыми обозначениями имеем:
Считаем, что оси цилиндров расположены в одной поперечной плоскости. Тогда в соответствии с формулами
получаем:
;
;
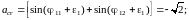
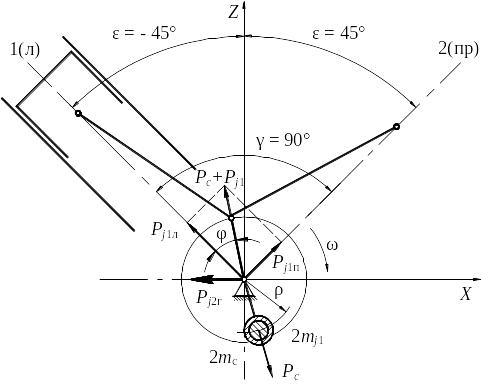
При этом
а
|
Рисунок 8. - Схема КШМ двухцилиндрового V-образного двигателя с одним кривошипом |
Результирующее значение определим по формуле:
где
–
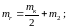
масса колена, приведенная к радиусу
кривошипа.
В соответствии с формулами
и
определяем коэффициенты выражений сил инерции поступательно движущихся масс:
Следовательно, получим
и 
Результирующая их равна
не зависит от угла поворота кривошипа и направлена по кривошипу, так как
и
Силы
и
действуют по осям левого и правого
цилиндров и смещены по фазе 90°. Суммирование
их даст результирующую, направленную
в любой момент по кривошипу.
Для силы Pj2 с учетом формул
и
получаем:
Следовательно,
Как видно, результирующая сил инерции поступательно движущихся масс второго порядка имеет только горизонтальную составляющую. Нетрудно убедится в том, что моменты Mj1 = 0 и Mj2 = 0.
Исходя из сказанного выше, уравновешивание рассматриваемого двигателя должно сводится к следующему:
1. Центробежная сила инерции Pс уравновешивается противовесами на щеках коленчатого вала.
2. Сила инерции поступательно движущихся масс первого порядка, направленная по кривошипу, также уравновешивается противовесами на щеках коленчатого вала.
3. Сила инерции поступательно движущихся масс второго порядка, действующая в горизонтальном направлении, может быть уравновешена по методу Ланчестера.
1.5. Статическая динамика
1.5.1. Остаточные силы инерции и моменты
Силы и моменты вращающихся и поступательно движущихся масс, действующие на двигатель, обычно определяют из их номинальных значений. За счет относительного расположения кривошипов и цилиндров, использование противовесов и специальных уравновешивающих механизмов может быть достигнута полная номинальная уравновешенность. Однако и при этом двигатель является фактически неуравновешенным. Вследствие отклонений от номинальных значений масс, радиусов кривошипов, углов заклинки кривошипов, и других параметров в многоцилиндровых двигателях получаются результирующие силы инерции, которые обычно называют остаточными. Указанные отклонения обусловлены технологическими причинами и имеют случайный характер.
Предельные отклонения значений масс для различных цилиндров двигателя будут одинаковыми, поэтому вращающиеся и поступательно движущиеся части могут иметь два разных цилиндров или кривошипов такое сочетание предельных отрицательных или положительных отклонений масс, что значение остаточной силы инерции получается максимальным.
Например, в двухцилиндровом рядном
двигателе с кривошипами, расположенными
под углом
,
получаем предельную остаточную силу
инерции поступательно движущихся масс
первого порядка, если в первом цилиндре
поступательно движущиеся массы
оказываются с предельным положительным
отклонением Δm,
а во втором с предельным отрицательным
Δm или наоборот.
Аналогичное явление может иметь место
и для других сил инерции и моментов от
них, а также случаев компоновки и числа
цилиндров двигателей.
Однако такой подход к оценке предельных отклонений сил инерции для двигателей массового производства оказывается упрощенным и не дает возможности получить представление о значениях остаточных сил инерции, так как в любом случае вероятность получения в данном двигателе предельных отклонений с соответствующими для различных цилиндров знаками весьма мала. В действительности в разных двигателях будет получаться случайное сочетание отклонений масс и других параметров, так что распределение их может быть оценено только на основе теории вероятности.