1.3.2. Моменты сил инерции поступательно движущихся масс, действующие в продольных плоскостях

Составляющие продольного момента сил инерции поступательно движущихся масс к-го порядка в вертикальной и горизонтальной плоскостях для двигателей однорядных и V-образных с вильчатыми и прицепными шатунами можно описать выражениями, полученными на основе рис. 1.

После преобразований получаем

; (1.28)

, (1.29)

где

Равнодействующие векторов момента

(1.30)

Угол вектора равнодействующей относительно вертикальной оси выражается соотношением

.

Начальные фазовые углы моментов сил инерции поступательно движущихся масс определим, приравняв их первые производные нулю. Так, для момента, действующего в вертикальной плоскости получим аналогично (1.26)

(1.31)

а для момента, действующего в горизонтальной плоскости – (1.27)

(1.32)

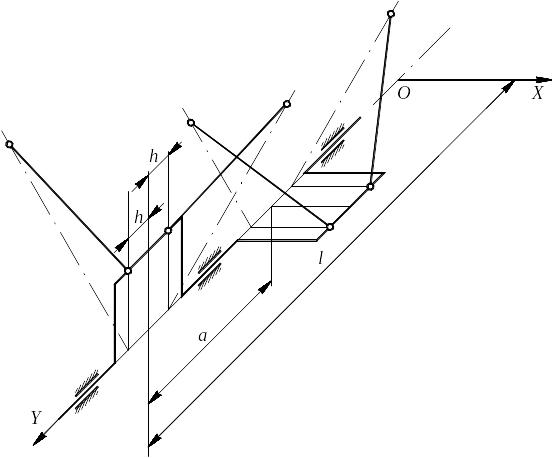
Рисунок 3. - Схема КШМ V-образного двигателя со смещенными цилиндрами правого блока относительно левого

1.3.3. Дополнительный момент сил инерции поступательно движущихся масс в V-образном двигателе с одинаковыми шатунами, действующими попарно на шатунные шейки

Cилы инерции поступательно движущихся масс направлены вдоль осей, которые у левых и правых цилиндров имеют относительное смещение в продольном направлении. Если эти силы взаимно неуравновешены, то появляется дополнительный момент. Он может быть учтен, если в выражениях (1.28) и (1.29) косинусных и синусных коэффициентов отразить эти смещения шатунов h относительно середины кривошипа (рис. 3). Они должны иметь знак плюс при смещении шатуна в направлении от середины коленчатого вала и наоборот. Вертикальная и горизонтальная составляющие этого момента выразятся соответственно

(1.33)

(1.34)

Далее, как обычно, определяем их равнодействующую и плоскость, в которой она действует.

1.4. Анализ уравновешенности двухцилиндровых двигателей

Уравновешенность двигателя является важной динамической характеристикой. Если она отсутствует, возникают повышенные нагрузки. Особенно значительны они при резонансных колебаниях двигателя, его узлов и деталей. Эти колебания могут распространяться на остов, кабину, рабочее место или кузов и салон автомобиля. В связи с этим снижается надежность указанных частей. Колебания двигателя и поверхностей машины, на которой он установлен, ухудшают комфортабельность и условия труда. Они могут приводить к быстрой утомляемости и даже заболеваниям различных органов человека. Не менее неприятен шум, вызываемый указанными колебаниями.

Уравновешенность определяется компоновочной схемой двигателя и использованием уравновешивающих устройств. Следует отметить также, что тенденция форсирования скоростного и нагрузочного режимов неизбежно вызывает необходимость повышения внимания к рассматриваемой проблеме. В связи с этим ниже дан анализ уравновешенности двигателей, с наиболее распространенными схемами компоновки. При необходимости такой анализ может быть выполнен и для любой другой схемы компоновки.