Центробежные силы инерции противовесов и моменты от них
Для уменьшения внутренней неуравновешенности коленчатого вала на продолжении щек кривошипов часто делают противовесы. Они могут быть на каждой щеке или на некоторых под соответствующими углами к плоскости первого кривошипа. Естественно, что их центробежные силы могут создавать неуравновешенную результирующую силу и момент, которые необходимо учитывать при оценке уравновешенности двигателя.
Это можно сделать на основе рассмотренной
выше расчетной схемы ( рис. 1.), если
вместо параметров, характеризующих
расположение кривошипов
и
принять аналогичные параметры для
противовесов –
и
.
По аналогии с выражениями (1.3) и (1.4) получим для результирующей центробежной силы инерции противовесов вертикальную и горизонтальную составляющие
(1.13)
(1.14)
В выражениях (1.13) и (1.14)
Используя ту же аналогию, получим для результирующей момента от центробежных сил инерции противовесов вертикальную и горизонтальную составляющие
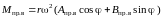(1.15)
и
(1.16)
где
В выражениях (1.13) и (1.14) масса i-го
противовеса
включена в косинусные и синусные
коэффициента, поскольку в общем случае
массы разных противовесов одного вала
различны. Отметим также, что это массы,
приведенные к радиусу кривошипа.
Параметры результирующей уравновешенности от центробежных сил определим по формулам
(1.17)
(1.18)
(1.19)
(1.20)
Выражения (1.17) – (1.20) используются для оценки неуравновешенности конкретного двигателя с учетом центробежных сил противовесов.
Сравнительная оценка уравновешенности двигателей с различными схемами компоновки производится обычно без учета влияния противовесов.
1.3. Силы инерции поступательно движущихся масс и моменты от них
1.3.1. Силы инерции поступательно движущихся масс
Силы инерции поступательно движущихся масс нормального кривошипно-шатунного механизма могут быть представлены рядом Фурье, члены которого являются гармоническими составляющими различных порядков:
где 
– соответственно масса поступательно
движущихся деталей, радиус и угол
поворота кривошипа.
Значения коэффициентов ряда Фурье представляют в функции отношения радиуса кривошипа к длине шатуна
Индекс у коэффициента А соответствует порядку гармоники.
Коэффициенты ряда Фурье для некоторых
значений
приведены ниже.
Как видно, с достаточной для большинства практических целей точностью можно рассматривать только гармоники 1-го и 2-го порядков. Получающаяся при этом погрешность составляет обычно менее 0,005 амплитудного значения гармоники первого порядка. В случае необходимости могут быть рассмотрены и гармоники более высоких порядков.
Результирующие значения сил инерции поступательно движущихся масс многоцилиндрового двигателя найдем, исходя из схемы и обозначений, приведенных на рис. 1.1. Получаем следующие выражения для определения вертикальной и горизонтальной составляющих сил инерции поступательно движущихся масс k – го моторного порядка:
(1.21)
(1.22)
После преобразований выражения (1.21) и (1.22) принимают вид
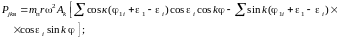
Заменив постоянные для данной схемы расположения цилиндров и кривошипов двигателя значения тригонометрических функций коэффициентами, получим следующие формулы:
(1.23)
и
(1.24)
где
В этих формулах при k
= 1
= 1, а при k = 2
.
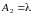Векторная равнодействующая значений вертикальной (1.23) и горизонтальной (1.24) составляющих сил инерции поступательно движущихся масс
(1.25)
В V-образных двигателях сила инерции поступательно движущихся масс первого порядка (k = 1) может иметь составляющие, зависящие и независящие от угла поворота коленчатого вала.
Более предпочтительным является второй случай, так как упрощается уравновешивание. Его можно осуществить, как и центробежной силы, т.е. противовесами на продолжении щек коленчатого вала.
Если сила инерции поступательно движущихся масс k-го порядка действует только в одной (вертикальной или горизонтальной) плоскости, то амплитудное значение их соответственно
при
и
при
Начальные фазовые углы определим, приравняв нулю первые производные по углу поворота вала
(1.26)
Аналогично для горизонтальных сил инерции поступательно движущихся масс
(1.27)
Некоторые поршневые двигатели имеют
дезаксиальные кривошипно-шатунные
механизмы, отличающиеся от рассмотренных
выше тем, что у них ось цилиндра смещена
относительно оси коленчатого вала. Это
смещение (дезаксиал) делают вправо или
влево. Величина его
(рис. 3). Относительный дезаксиал у
разных двигателей составляет обычно k
= e/r
= 0,03...0,2.
Такие двигатели имеют некоторые особенности в кинематике, динамике и рабочем процессе. Так, например, давление поршня (при смещении его вправо) на левую стенку цилиндра во время рабочего хода уменьшается, а на правую во время хода сжатия увеличивается. Это способствует более равномерному износу цилиндра. При дезаксиале увеличивается ход поршня, а следовательно, рабочий объем и продолжительность впуска, что несколько увеличивает мощность двигателя.
Определенные преимущества дезаксиала связаны с меньшими, чем в осевом механизме, скоростью поршня и износом цилиндра в области ВМТ, где они имеют максимальное значение. Кроме того, улучшаются показатели цикла, так как сгорание завершается при меньшем объеме надпоршневого пространства.
В современных двигателях обычно дезаксиал осуществляется смещением оси поршневого пальца относительно оси поршня при расположении осей цилиндра и коленчатого вала в одной плоскости. Равнодействующие сил давления газов и инерции создают при этом момент относительно оси пальца, так они не проходят через нее. Поэтому поршень в области ВМТ перемещается от одной стенки к другой с поворотом, вследствие чего уменьшается удар о стенку цилиндра и снижаются вибрация и шумность работающего двигателя.
Рассмотрим влияние дезаксиала на силы инерции поступательно движущихся масс исходя из известного выражения
Оно отличается от выражения для определения силы инерции центрального механизма только по составляющей гармоники первого порядка
где k=e/r - дезаксиал.
Амплитудное значение гармоник первого порядка
При k = 0,3 и = 0,25 имеем
У механизма без дезаксиала
Таким образом, даже при таком значительном дезаксиале амплитуды гармоник первого порядка сил инерции поступательно движущихся масс увеличиваются всего на 0,28 %.