Глава 2. Расчет уравновешенности

В расчетной части работы проведём сравнение двухцилиндрового однорядного двигателя с кривошипами направленными под углом 360⁰ и двухцилиндрового однорядного двигателя с кривошипами под углом 180⁰, определим наилучшую уравновешенность, выявим преимущества и недостатки каждой схемы.

Схема с кривошипами направленными в одну сторону может применяться только в четырёхтактных двигателях, так как только для этих двигателей обеспечивается равномерное чередование вспышек через 360⁰ угла поворота коленчатого вала.

Схема с расположением цилиндров под углом 180⁰ применяется как для двухтактных, так и для четырехтактных. В двухтактных двигателях при такой схеме обеспечивается равномерное чередование вспышек через каждые 180⁰ поворота коленчатого вала.

2.1. Расчет уравновешенности двигателя с кривошипами направленными под углом 3600

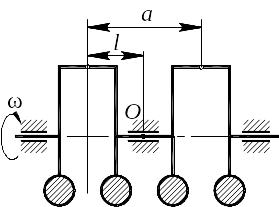
Рисунок 9. - Схема коленчатого вала двухцилиндрового двигателя с кривошипами под углом 3600.

В соответствии с обобщенной схемой (рис. 1) получаем следующие параметры:

Принимаем: a = 89 мм; r = 35,5 мм = 0,00355 м; λ = 0,29;

m_r = 3,7 кг; ω = 596,9 ; m_п = 1,285 кг;

Находим значения косинусного и синусного коэффициентов

Вертикальная и горизонтальная составляющие центробежной силы инерции

P_cв = 2m_rrω²cosφ = 2∙3,7∙0,00355∙596,9²∙1 = 9,3 кН

P_cr = 2m_rrω²sinφ = 2∙3,7∙0,00355∙596,9²∙0 = 0

а их результирующая

P_c = P_cв + P_cr = 9,3 + 0 = 9,3 кН

и действует по радиусу кривошипа.

Очевидно, что момент центробежных сил инерции вращающихся масс

Силы инерции возвратно-поступательно движущихся масс и моменты от них определяются выражениями:

P_j1в = 2m_пrω²cosφ = 2∙1,285∙0,00355∙596,9² ∙1 =3,25 кН ;

P_j1r = 0;

ΣP_j1 = P_j1в + P_j1r = 3,25 + 0 = 3,25 кН.

P_j2в = 2m_пrω²λcos2φ = 2∙1,285∙0,00355∙596,9² ∙ 0,29∙1 = 0,94 кН ;

P_j2r = 0 ;

ΣP_j2 = P_j2в + P_j2r = 0,94 + 0 = 0,94 кН.

M_j1 = 0.

M_j2 = 0.

Уравновешенность механизма может быть оценена непосредственным суммированием сил, так как они расположены в одной плоскости и одинаковы по величине.

2.2. Расчет уравновешенности двигателя с кривошипами под углом 180°

Рисунок 10. - Схема коленчатого

вала двухцилиндрового двигателя

с кривошипами под углом 180⁰.

_{Учитывая, что}

Принимаем: a = 89 мм; r = 35,5 мм = 0,00355 м; λ = 0,29;

m_r = 3,7 кг; ω = 596,9 ; m_п = 1,285 кг; l = 44,5 мм.

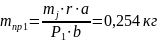; p₁ = 0,01 м; b = 0,16 мм;

= 0,033 кг; p₂ = 0,01 мм.

P_cв = m_rrω²(a_cв cosφ+ b_cв sinφ) = 3,7∙0,00355∙596,9² ∙(0+ 0) = 0; (2.1)

P_cr = m_rrω²(a_cr cosφ+ b_cr sinφ) = 3,7∙0,00355∙596,9² ∙(0+ 0) = 0. (2.2)

где

a_cв = Σ cos(φ_1i + ε₁) = cos(φ₁₁ + ε₁) + cos(φ₁₂ + ε₁) = cos(0 + 0) + cos(180 + 0) =0 ;

b_cв = - Σ sin(φ_1i + ε₁) = - (sin(φ₁₁ + ε₁) + sin(φ₁₂ + ε₁)) = - (sin(0 + 0) + sin(180 + 0)) = 0 ;

a_cr = Σ sin(φ_1i + ε₁) = sin(φ₁₁ + ε₁) + sin(φ₁₂ + ε₁) = sin(0 + 0) + sin(180 + 0) = 0

b_cв = Σ cos(φ_1i + ε₁) = cos(φ₁₁ + ε₁) + cos(φ₁₂ + ε₁) = cos(0 + 0) + cos(180 + 0) =0.

Равнодействующая вертикальной и горизонтальной составляющих

P_c = (2.3)

или

P_c = m_rrω²

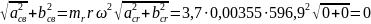
Моменты сил инерции вращающихся масс. Составляющие момента сил инерции вращающихся масс, относящихся к i-му цилиндру и действующие в вертикальной и горизонтальной плоскостях можно определить из выражений

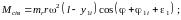(2.4)

(2.5)

Формулы для определения результирующих вертикальной и горизонтальной составляющих момента получены на основе выражений (2.6) и (2.7):

M_cв = m_rrω²Σ(l-y_1i)cos(φ+φ_1i+ ε₁) = m_rrω²((l-y₁₁)cos(φ+ φ₁₁+ ε₁)+ (l-y₁₂)cos(φ+ φ₁₂+ ε₁)) = ((0,00445- 0)cos(0+ 0+ 0)+ (0,00445- 0,0089)cos(0+ 180 + 0)) = 41,6 Нм;

M_cr = m_rrω²Σ(l-y_1i)sin(φ+φ_1i+ ε₁) = = m_rrω²((l-y₁₁)sin(φ+ φ₁₁+ ε₁)+ (l-y₁₂)sin(φ+ φ₁₂+ ε₁)) = ((0,00445- 0)sin(0+ 0+ 0)+ (0,00445- 0,0089)sin(0+ 180 + 0)) = 0.

В результате преобразований, аналогичных выполненным ранее, имеем

(2.6)

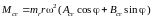(2.7)

где

A_св = Σ (l-y_1i)cos(φ_1i+ε₁) =( l-y₁₁)cos(φ₁₁+ε₁)+ (l-y₁₂)cos(φ₁₂+ε₁) =

( 0,00445-0)cos(0+0)+ (0,00445-0,0089)cos(180+0) = 0,0089 мм ;

A_сr = Σ (l-y_1i)sin(φ_1i+ε₁) =( l-y₁₁)sin(φ₁₁+ε₁)+ (l-y₁₂)sin(φ₁₂+ε₁) =

( 0,00445-0)sin(0+0)+ (0,00445-0,0089)sin(180+0) = 0;

B_св = -Σ (l-y_1i)sin(φ_1i+ε₁);

B_сr = Σ (l-y_1i)cos(φ_1i+ε₁).

или

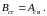
тогда B_св = 0;

B_сr = 0,0089.

Векторная равнодействующая моментов

M_c = 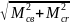= = 41,6 Нм (2.8)

Угол между векторной равнодействующей моментов и вертикальной осью определяем, исходя из соотношения

= 1

Подставив выражения (2.7) в эту формулу, получаем

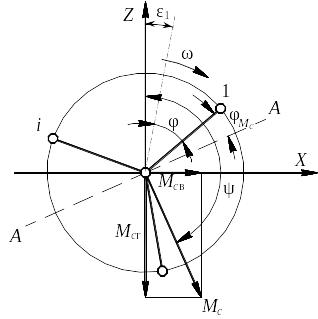
Рисунок 11. - Определение угла между векторной равнодействующей моментов и вертикальной осью

С другой стороны, исходя из схемы, приведенной на рис. 1, имеем

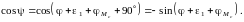
Разложим синус суммы углов и :

(2.9)

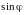Приравняв в (2.8) и (2.9) значения перед и , имеем

и

откуда

Как видно на схеме, 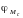- угол между плоскостью действия момента AA и плоскостью первого кривошипа. Зная этот угол, можно правильно расположить противовесы, уравновешивающие момент центробежных сил инерции.