17.Понятие определенного интеграла, его геометрический и экономический смысл.

Геометрич смысл опр инт-ла. Если f(x) непрерывн. и положит-а на отр-ке от а до в, то инт предст-ет собой S криволин трапеции, огранич-ой линиями y=0, x=a, x=b, y=f(x). Экономич. Опр. Инт. Исп-ся при рассмотр-и задач, в к-х нужно сумм-ть рез-ты возд-я нек-ой перемен-ой велич., на заданном промеж-ке. Напр., если y=f(x)-пред. изд-ки пр-ва, где х-объём пр-ва, то -изд-ки пр-ва при изменении объёма от а до b.

21.Теорема об интеграле с переменным верхним пределом. (дополнительный вопрос)

Произв-я опр. инт-ла от непрерывн. ф-ии по верхнему пределу = знач. подинт. ф-ии.

22.Формула Ньютона-Лейбница.

Для неопр. ф-ии y=f(x) на конечн. отр-ке, опред. инт-л нах-ся как первообр-ая ф-ии f(x) в пред-х от а до b. Ф-ла справедлива при усл-х: y=f(x) непрерывна на (а,в), (а,в) должен быть конечным.

Если ф-ция непрерывна на отрезке [a, b] и F(x)-какая-либо первообразная для на этом отрезке,то справедлива формула Ньютона-Лейбница:

23.Замена переменной в определенном интеграле. Интегрирование по частям.

пусть ф-ия x= определена непрерывно, диф-мо и монотон. на отр-ке , , и ф-я f(x) непрер-на на отр. , тогда . Если u(x), v(x) непрер диф ф-ии, то ….

19.Свойства определенного интеграла: теорема об интегрировании неравенств, теоремы об оценке интеграла.

1. 

2. 

3. ,где к-постоянная.

4. Если всюду на отрезке [a, b] функция неотрицательна то ,

а если то .

5. Если на отрезке [a, b] функции и удовлетворяют условию , то ---теорема об интегрировании неравенств.

6. Если на отрезке [a, b] функция удовлетворяет условию , то определенный интеграл удовлетворяет неравенству .

7. Определенный интеграл от функции , непрерывной на отрезке [a, b], равен значению подынтегральной функции в некоторой «средней» точке с промежутка интегрирования, умноженному на длину этого промежутка:

8. Если на отрезке [a, b] функция непрерывна и Ф(х) 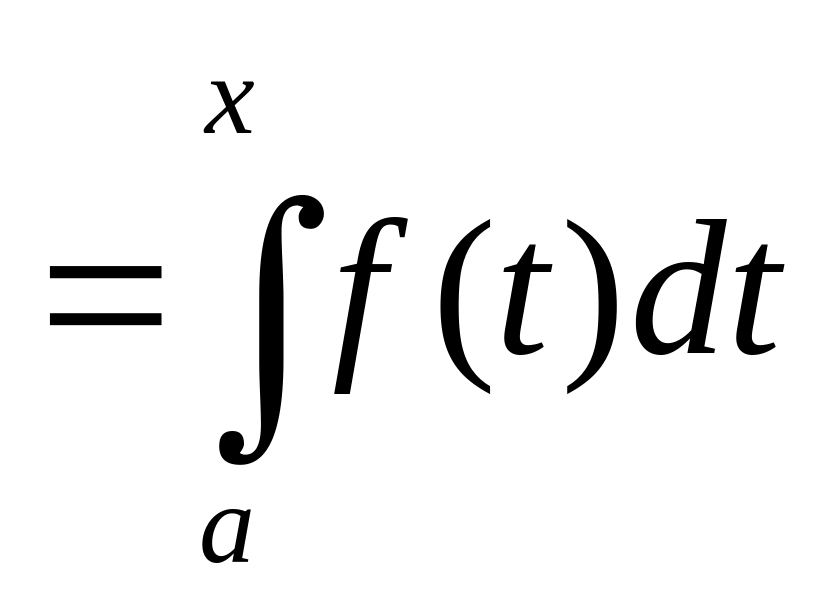,то справедливо равенство Ф’(х)= , т.е. производная опр.интеграла от непрерыв.ф-ции по его переменному верхнему пределу х существует и равна значению подынтегр.функции при том же х.

Если ф-ция непрерывна на отрезке [a, b] и F(x)-какая-либо первообразная для на этом отрезке,то справедлива формула Ньютона-Лейбница:

20.Теорема о среднем. Ее геометрическая и экономическая интерпретация.

1. Теорема о среднем

Первая теорема о среднем

( - среднее значение функции).

Если f непрерывна, то

Вторая теорема о среднем

Если f, g непрерывны, а g не меняет знак, то

Формула Бонне

(g монотонна).

24.Вычисление площадей плоских фигур. Вычисление объемов тел вращения. Вычисление длины дуги кривой.

Для вычисл. S криволин трап, огранич сверху и снизу прямыми y=f(x) y=g(x) cоотв исп ф-ла . Объём. Пусть нек-е объём-е тело огранич плоскостыми х=а и х=в, и известна ф-я y=S(x), опис-я S попереч сеч в завис-ти от х. то ф-ла ,если дугу повращ-ть вокруг оси Ох, то , если вокруг Оy, то . Длина дуги

25.Понятие несобственных интегралов I рода. Пример интеграл Дирихле I рода.

НИ1-это опр инт-л от непереывн ф-ии на бесконеч отр-ке интегрир-я. Бескон отр инт-я может быть 3-ёх видов 1. 2. 3. . По опред-ю НИ1 это предел от опред инт-ла . На 1-ом этапе вычисл опр инт от а до в по ф-ле Н-Л, на 2-ом предел получ-ой ф-ии зависящей от b , т.к. это этап вычисл-я пред-ла, то от его реализ-ии зависит ответ. Если получено число, то НИ1 сходится к этому числу; если то расх-ся.