Мгновенная ось вращения

Мгновенная ось вращения — геометрическое место точек, скорость которых в данный момент времени равна нулю. Мгновенная ось вращения — ось бесконечно малого поворота тела, определяется из уравнения (рис.1.7):

где М — произвольная точка, лежащая на оси вращения.

Уравнения мгновенной оси в неподвижной системе координат можно записать в виде 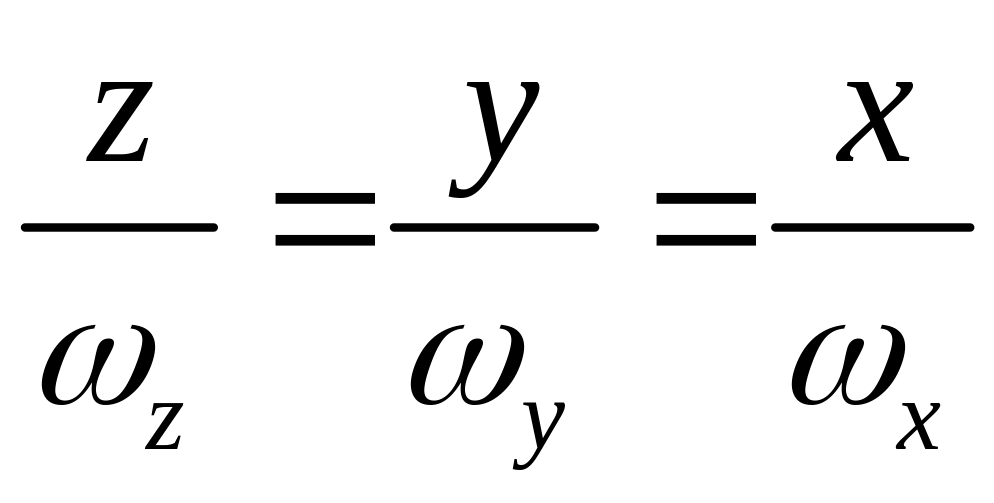, или в подвижной системе координат

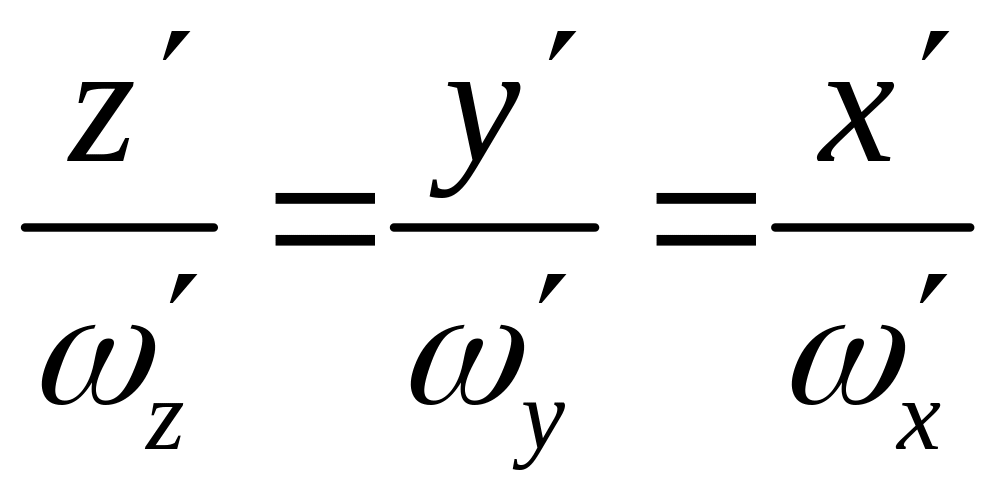
Рис. 1. 7. Скорость и ускорение точки при сферическом движении твердого тела

Перемещаясь в пространстве и внутри тела, Мгновенная ось опишет собой конические поверхности, которые называются соответственно неподвижным и подвижным аксоидами. Для получения уравнений этих поверхностей необходимо из уравнений мгновенной оси вращения исключить время.

Подвижный аксоид катится без проскальзывания по неподвижному. Данный вывод следует из равенства нулю скоростей точек мгновенной оси вращения, которая является в текущий момент общей для неподвижного и подвижного аксоидов.

Ускорение точки тела

Ускорение произвольной точки тела может быть определено по формуле Ривальса:

где — вращательное ускорение, направленное перпендикулярно к векторам и (рис.1.7);

— угловое ускорение тела, совершающего сферическое движение. Вектор углового ускорения направлен вдоль мгновенной оси ускорений, которая определяется из условия равенства нулю вращательного ускорения произвольной точки оси ускорений;

— осестремительное ускорение, перпендикулярное векторам и (рис.1.7).

Составное движение точки

Механические явления по–разному фиксируются в различных системах отсчёта. Наблюдатели, связанные с разными системами координат, по–разному воспринимают одно и то же объективное механическое явление. Главной задачей кинематики составного движения является установление связи между кинематическими характеристиками, полученными в различных системах отсчёта. Одна из этих систем условно называется неподвижной системой. Вторая — подвижной системой отсчета (рис.1.8).

Движение относительно условно неподвижной системы координат называется абсолютным. Движение точки относительно системы координат , движущейся, в свою очередь, относительно условно неподвижной (рис.1.8), называется относительным. Переносным движением называется движение подвижной системы . Переносным движением точки М называется движение точки , принадлежащей подвижной системе координат и совпадающей в данный момент времени с точкой . Различаются абсолютные, относительные, переносные траектории, скорости и ускорения точки  .

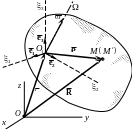
Рис. 1. 8. Составное движение точки

Абсолютной или относительной траекторией, скоростью и ускорением называется траектория, скорость и ускорение в абсолютном или относительном движении.

Переносной траекторией точки называют элементарный отрезок траектории точки подвижной системы координат, с которой в данный момент совпадает исследуемая точка. Переносной скоростью и ускорением точки называется скорость и ускорение той точки подвижной системы координат, с которой в данный момент времени совпадает исследуемая точка.

Относительные скорость и ускорение будем обозначать и . Индекс "r" — начальная буква французского слова relative (относительный).

Переносные скорость и ускорение будем обозначать и . Индекс "е" — от французского слова d'entainement (переносный).