Сферическое движение твердого тела Определение сферического движения.

Сферическим движением называется движение твердого тела имеющего одну неподвижную точку (рис.1.6). Описание такого движения имеет первостепенное значение при анализе работы гироскопов, кораблей, самолётов, снарядов, ракет и небесных тел. Тело, совершающее сферическое движение имеет три степени свободы.

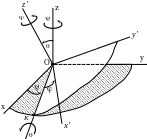
Рис. 1. 6. Сферическое движение твердого тела (Углы Эйлера)

Тело, совершающего сферическое движение, привести в заданное положение можно с помощью трех конечных поворотов, называемых углами Эйлера (рис.1.6). Первый поворот произведём вокруг оси неподвижной системы координат угол прецессии . Второй поворот произведём вокруг линии узлов на угол нутации . Третий поворот осуществляется вокруг оси на угол собственного вращения . После третьего поворота тело и оси подвижной системы координат связанные с ним займут заданное положение. При движении тела в каждый момент времени углы Эйлера являются функциями времени:

Эти зависимости называются кинематическими уравнениями сферического движения.

Вектор, определяющий положение точки в неподвижной и подвижной системах отсчета, равен

,

а координаты точки связаны при помощи матрицы преобразования

где

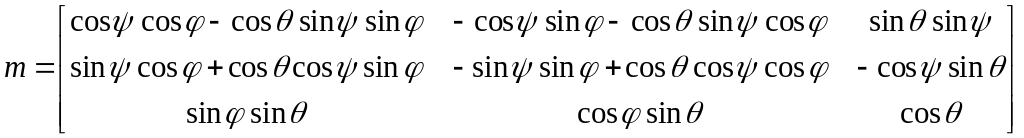
Теорема Эйлера-Даламбера о конечном повороте

Любое перемещение твёрдого тела, имеющего одну неподвижную точку, можно осуществить одним конечным поворотом вокруг оси, проходящей через эту точку.

Для чего нам нужна эта теорема? Чтобы ответить на следующий вопрос: можно ли бесконечно, малые углы поворотов, произведённых последовательно друг за другом, складывать по правилу параллелограмма (как векторы)?

Угловая скорость, угловое ускорение

В ведём "вектор" малого поворота , равный по величине углу поворота и направленный по оси вращения в такую сторону, чтобы, глядя с его острия видеть вращение происходящим против часовой стрелки. Вектор малого перемещения при таком бесконечно малом вращении может быть найден по формуле

.

Произведём два последовательных поворота. После первого поворота на угол , вектор переместится в положение

.

После второго поворота на угол вектор переместится в положение

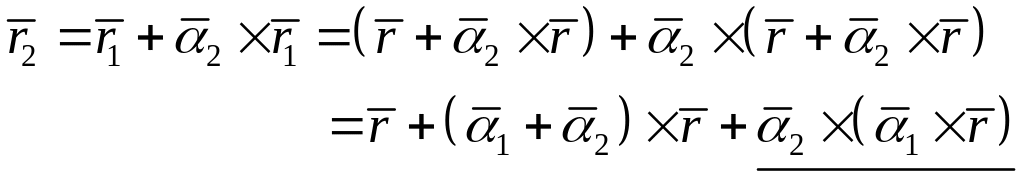
В силу малости и подчёркнутым слагаемым можно пренебречь как величиной более малого порядка, чем остальные компоненты формулы.

.

Но по теореме Эйлера-Даламбера суммарное движение можно записать в виде формулы описывающей один поворот на угол :

.

Сравнивая последние формулы между собой, получим

.

Т. е. бесконечно малые углы поворота можно считать векторами и складывать по правилу параллелограмма.

Введём определение угловой скорости и углового ускорения:

.

Угловое ускорение равно линейной скорости конца вектора угловой скорости .

Т. к. вектор может быть представлен в виде суммы двух или нескольких поворотов

Используя в качестве описанных углов углы Эйлера, получим важную формулу:

.

Скорость точки тела, участвующего в сферическом движении

Найдем скорость точки тела, участвующего в сферическом движении. Эта формула носит имя Эйлера.

Вычислим предел отношения малого перемещения точки к малому промежутку времени, в течение которого он происходил при :

.

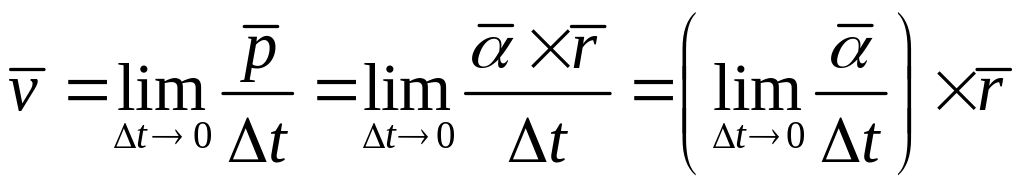Окончательно

где угловая скорость тела относительно мгновенной оси вращения.

Используя формулы аналитической геометрии, векторное произведение представим в виде

.

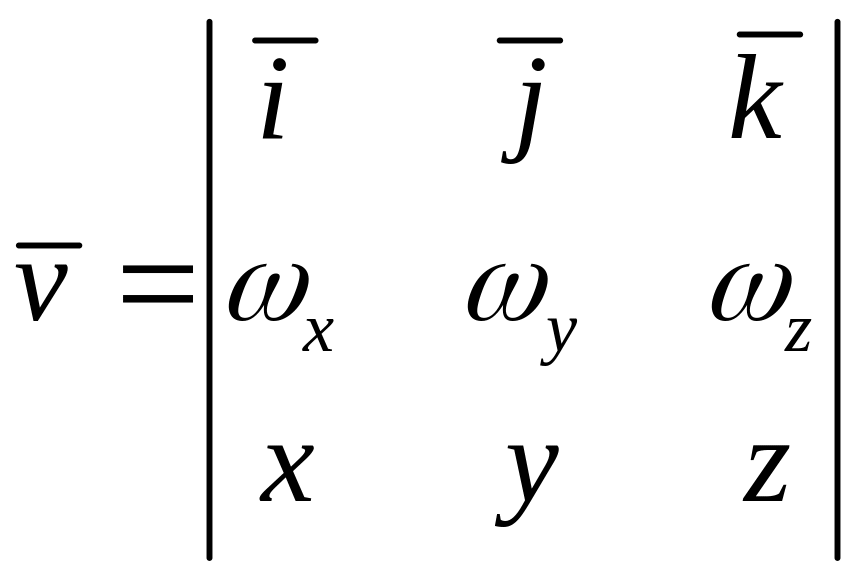Раскрыв определитель, получим формулы Эйлера в неподвижной системе координат

Аналогично можно получить формулы Эйлера в подвижной системе координат, для чего нужно формально произвести в предыдущих соотношениях замену на , на , и т. д.