Исследование вынужденных колебаний
Для дальнейшего исследования вынужденных колебаний, с целью упрощения преобразований, можно, не нарушая общности, принять нулевые начальные условия:
.
Уравнение вынужденных колебаний в этом случае примет вид
,
где
,
.
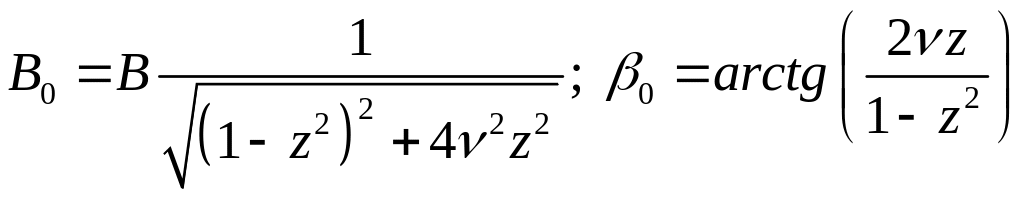Резонанс
Явление, возникающее
при совпадении частот вынужденных и
свободных колебаний механической
системы, называется резонансом. В этом
случае значение коэффициента расстройки
.
Уравнение движения, сдвиг фазы и
амплитуда вынужденных колебаний
определяются равенством
,
где
.
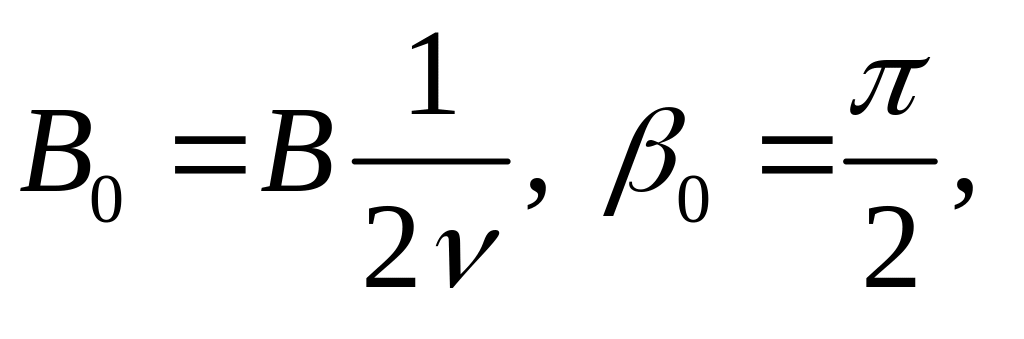
Ошибка! Закладка не определена.
Рис. 3. 15 Резонансные колебания при наличии сопротивления.
Здесь, при наличии сопротивления
движению и любом значении коэффициента
демпфирования
,
амплитуда вынужденных колебаний
остается конечной величиной. График
такого движения представлен на
рис. 3. 15.
При отсутствии сопротивления
уравнение колебаний теряет физический
смысл, т.к. амплитуда вынужденных
колебаний становится равной бесконечности.
Для получения уравнения, описывающего
явление резонанса при отсутствии
сопротивления, разложим величину
в ряд по степеням
и перейдем к пределу при
,
.
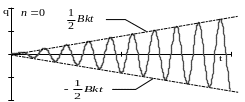
Рис. 3. 16 Резонансные колебания при отсутствии сопротивления.
Уравнение движения примет вид:
.
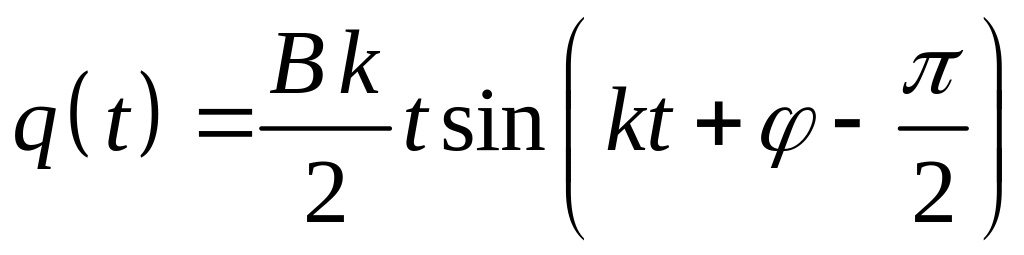Данное выражение показывает, что амплитуда вынужденных колебаний возрастает пропорционально времени. Частота и период вынужденных колебаний при резонансе и отсутствии сопротивления равны частоте и периоду свободных колебаний механической системы (см. рис. 3. 16).
Биения.
При частоте возмущающей силы, близкой к частоте свободных колебаний, наступает явление, называемое биениями.
Особенно ярко это
явление проявляется при отсутствии
сопротивления движению (см. рис. 3. 17),
т. е. при
и
.
В этом случае получим
,
где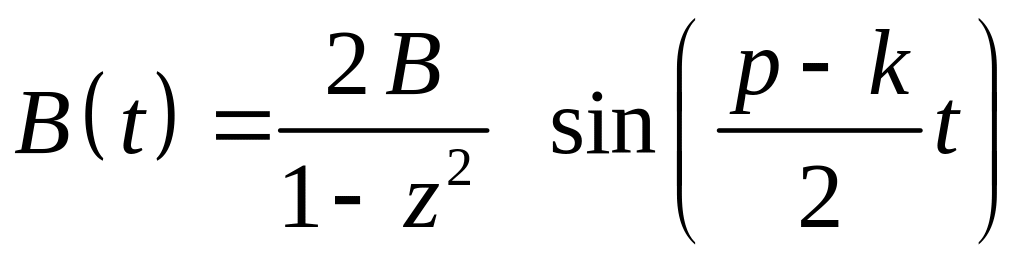
.
Ошибка! Закладка не определена.
Рис. 3. 17 Биения при отсутствие сопротивления.
Ошибка! Закладка не определена.
Рис. 3. 18 Биения при наличии сопротивления.
Движение, определяемые данным уравнением,
можно рассматривать как колебания
частоты
и периода
,
амплитуда которых
является периодической функцией с
периодом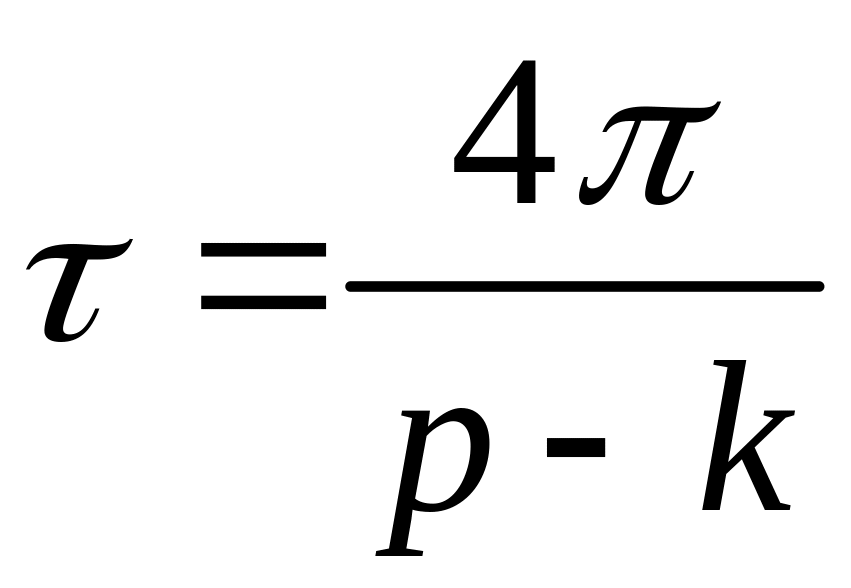
.
Так как
,
то период
велик по сравнению с периодом вынужденных
колебаний
.
Аналогичное явление можно получить и при наличии сопротивления движению (см. рис. 3. 18), в том случае, если коэффициент сопротивления достаточно мал.
Критерии и условия, используемые при исследовании колебательных движений механических систем
Теория вынужденных колебаний имеет много важных приложений в различных областях науки и техники. При проектировании конструкции, подверженной воздействиям возмущающих сил, чаще всего стараются подобрать соотношения размеров и масс конструкции, чтобы по возможности отодвинуть условия нормального режима работы ее от резонансных условий. При этом используется важное свойство колебательного процесса, позволяющее при больших значениях возмущающей силы сделать амплитуду вынужденных колебаний очень малой за счет подбора соотношений между частотами p и k.
Из анализа уравнения вынужденных колебаний можно сделать следующие выводы:
вынужденные колебания при наличии сопротивления с течением времени, величина которого зависит от степени сопротивления, происходят с частотой возмущающей силы, поскольку
,
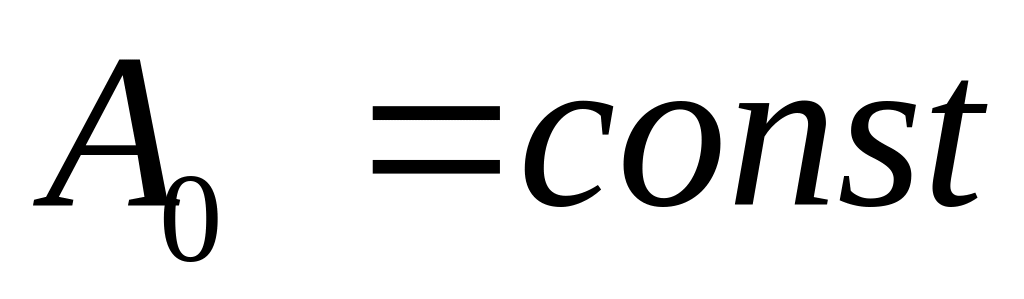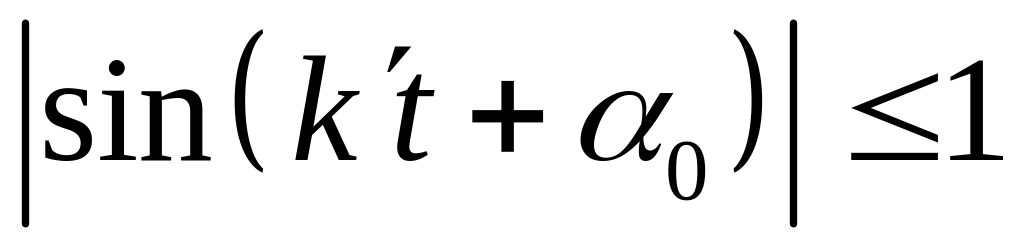при любом значении t, а
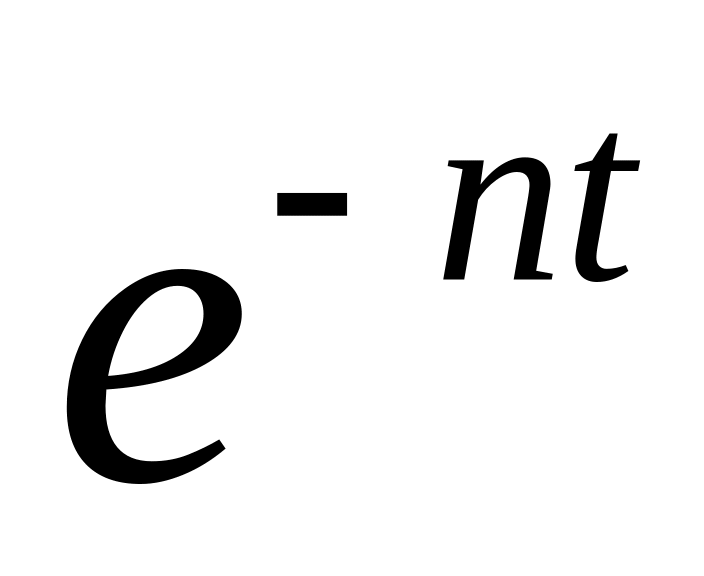— быстро убывающая функция.амплитуда вынужденных колебаний от начальных условий и времени не зависит. При резонансе
,
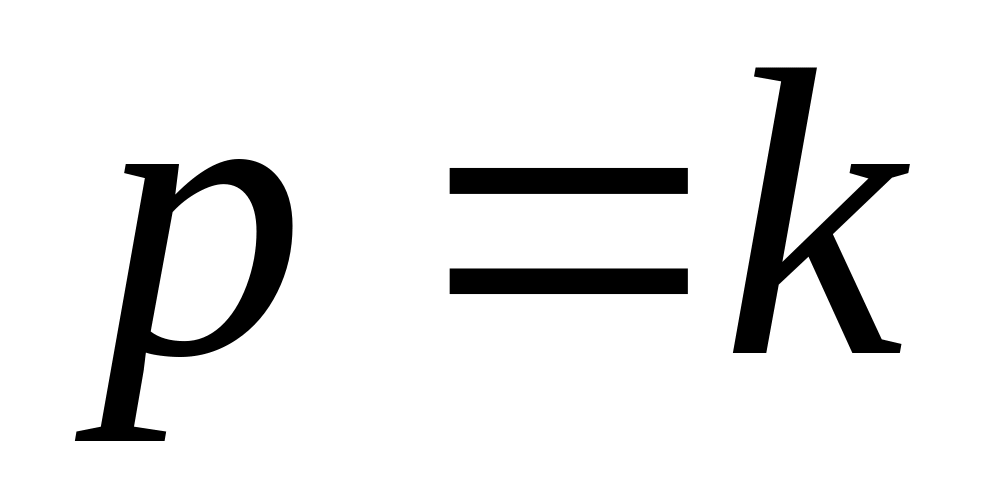амплитуда вынужденных колебаний
остается конечной и притом не самой
большой из возможных значений для
данной системы.в вынужденных колебаниях при наличии сопротивления всегда имеет место сдвиг фазы колебаний по сравнению с фазой возмущающей силы. При резонансе, когда , сдвиг фазы принимает значение равное
.
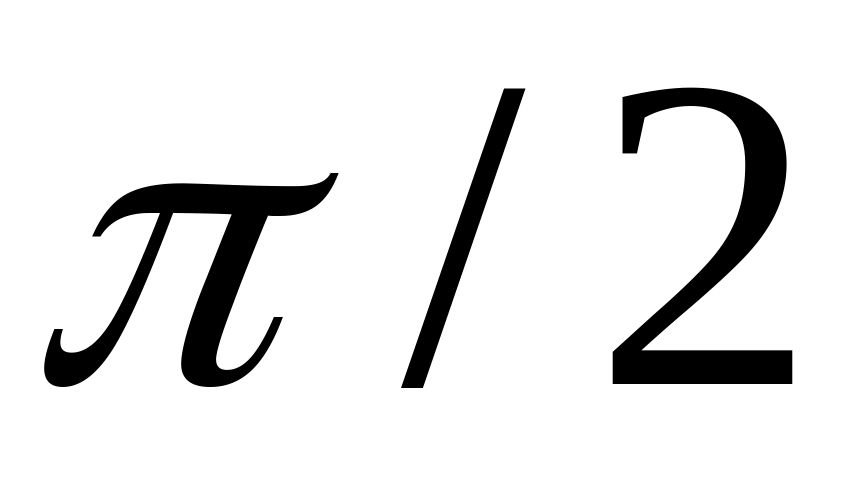В случае малого сопротивления в области
достаточно удаленной от резонанса
когда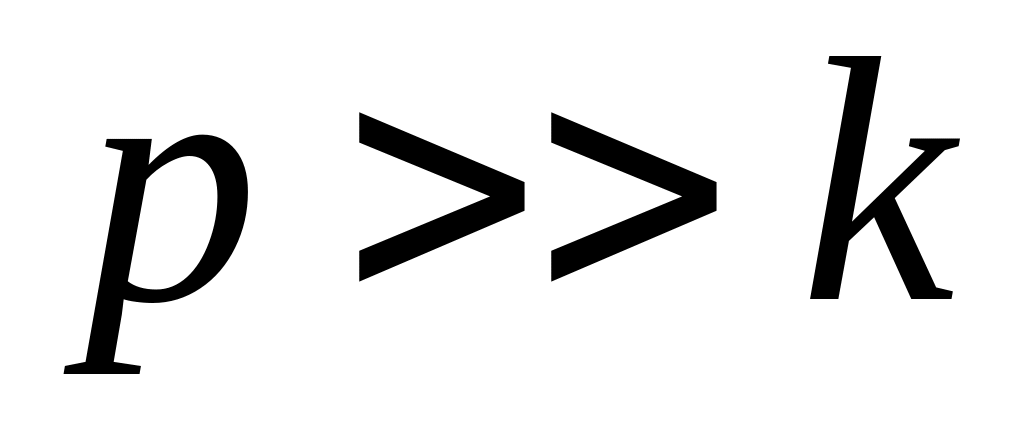
,
значения фазового смещения стремятся
к величине
,
а при
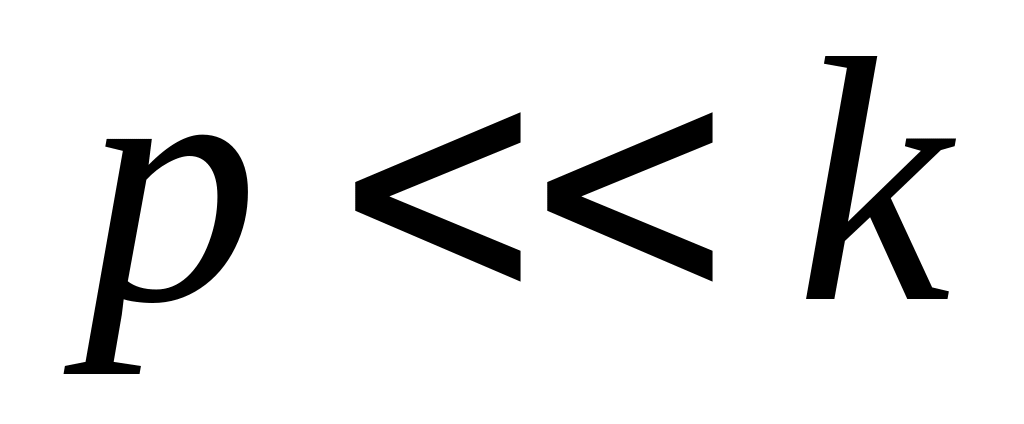стремится к нулю.
При исследовании колебательных процессов механических систем используются два основных критерия: коэффициент динамичности и коэффициент передачи силы.