Ошибка! Закладка не определена.
Рис. 3. 9 График свободных колебаний без учета сопротивления
Величина обратная частоте свободных
колебаний называется периодом колебаний
и определяется выражением
.
Затухающие колебания системы
Если на любую точку механической системы
с наложенными стационарными голономными
связями, кроме упругой силы, действует
сила сопротивления пропорциональная
первой степени скорости
,
то уравнение Лагранжа II
рода можно записать в виде
.
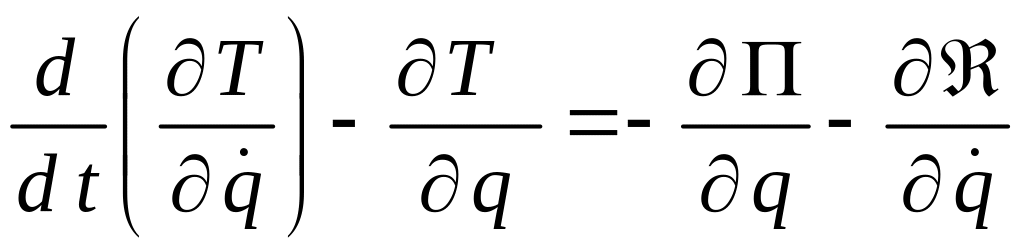Подставляя выражения для кинетической, потенциальной энергии и диссипативной функции в уравнение Лагранжа II рода, получим
где
— коэффициент демпфирования (затухания).
Т.к. корни характеристического уравнения соответствующие данному дифференциальному уравнению определяются выражениями
,
то его решение зависит от соотношений
между коэффициентами
и
:
Ошибка! Закладка не определена.
Рис. 3. 10 Апериодическое движение при большом сопротивлении
—
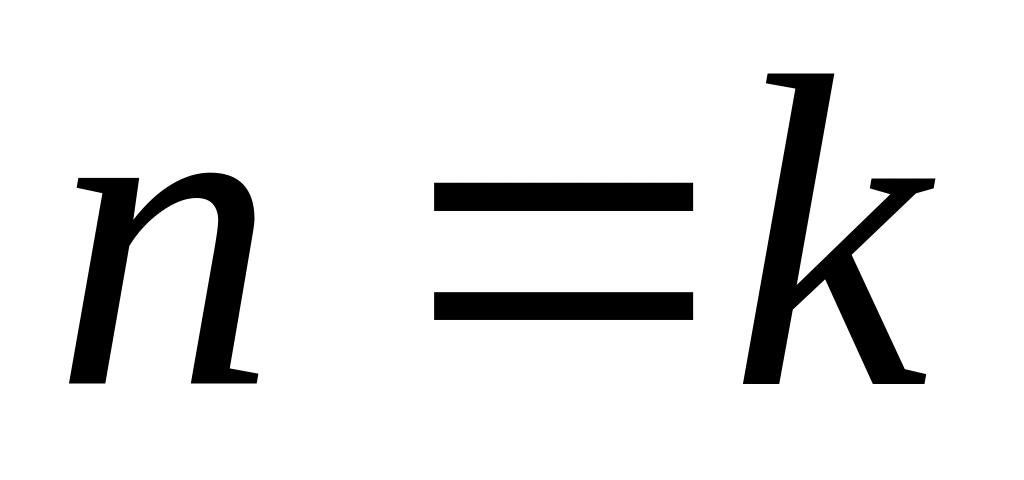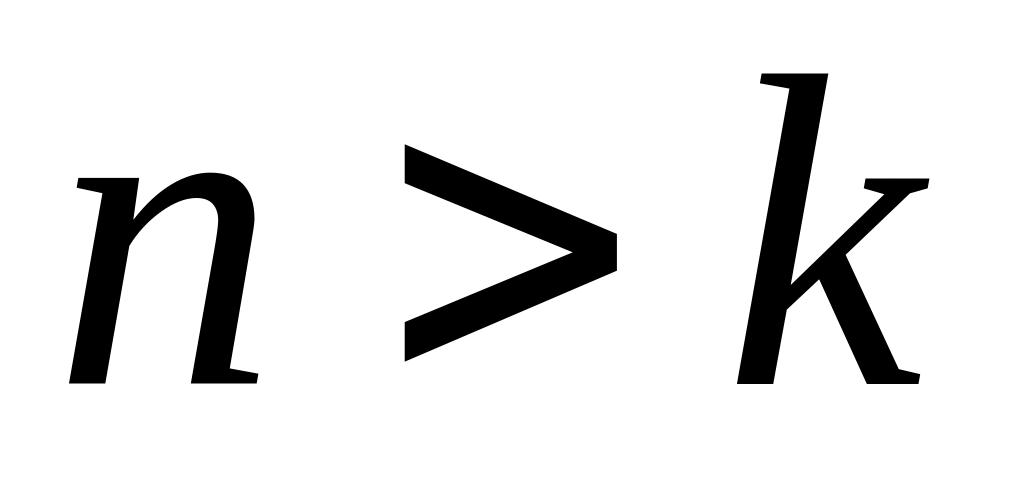решение имеет вид (рис. 3. 10):
;
—
решение имеет вид (рис. 3. 10):
,
где
— также как и в случае колебательного
движения без сопротивления, константы
интегрирования, определяемые из
начальных условий.
При движение механической системы имеет апериодический характер, типичный график которого, изображен на рис. 3. 10.
—
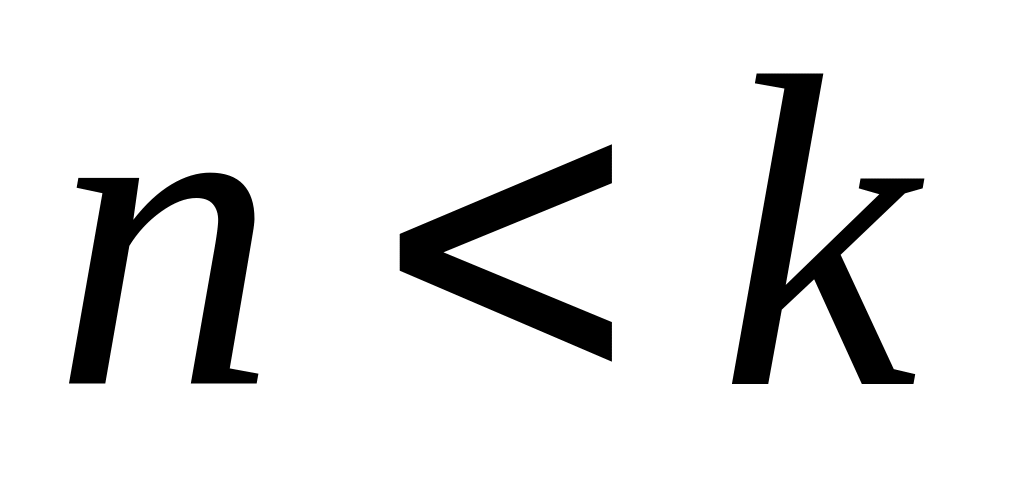(случай малого сопротивления) решение
имеет вид (рис. 3. 11):
или
.
Здесь
— называется частотой свободных
затухающих колебаний,
—
относительный коэффициент затухания,
константы интегрирования
определяются из начальных условий
:
,
.
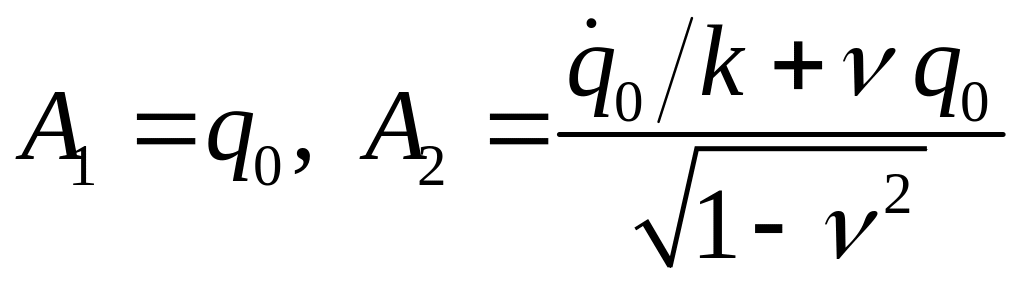Величина
— как и в случае колебаний без учета
сопротивления, называется начальной
фазой колебаний. Коэффициент
определяет координату пересечения
образующей графика
—
с
осью
.(см.
Рис. 3. 11)
Ошибка! Закладка не определена.
Рис. 3. 11 Свободные затухающие колебания.
Период затухающих колебаний определяется соотношением
.
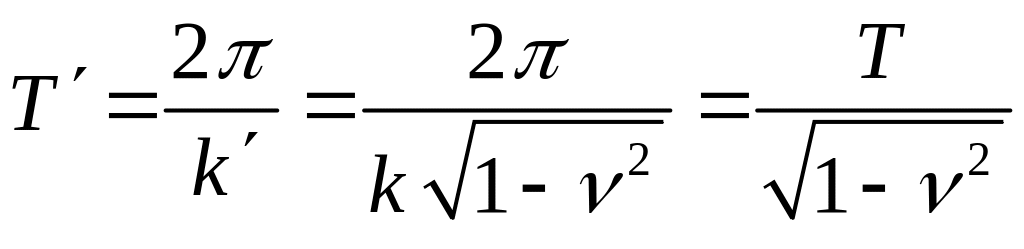Степень затухания колебательного
движения определяется декрементом
колебаний
,
который определяется отношением двух
последовательных максимумов кривой
или логарифмическим декрементом
:
.
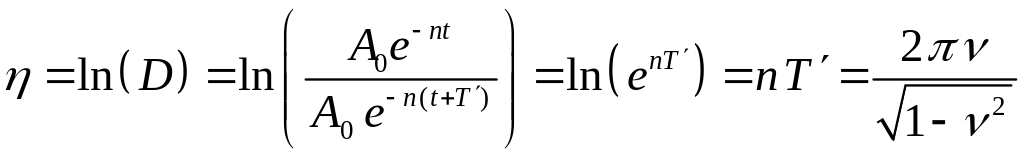Вынужденные колебания системы
Пусть на некоторую точку механической
системы с наложенными стационарными
голономными связями, кроме упругой
силы и силы сопротивления пропорциональной
первой степени скорости, действует
периодическое возмущение. Характер
такого возмущения может иметь разные
причины. Наиболее часто встречаются
случаи силового и кинематического
возмущения. В качестве примера рассмотрим
динамическую модель машины, установленной
на фундаменте (рис. 3. 12). Машина
массой m является
амортизируемым объектом, а фундамент
– основанием. Амортизатор, помещенный
между объектом и основанием, имеет
приведённый коэффициент жёсткости
и приведённый коэффициент демпфирования
.
На рис. 3. 12 (а) представлен случай
силового возмущения, а на рис. 3. 12
(б) — случай кинематического возмущения.
При силовом возмущении уравнение Лагранжа II рода для такой системы можно записать в виде
,
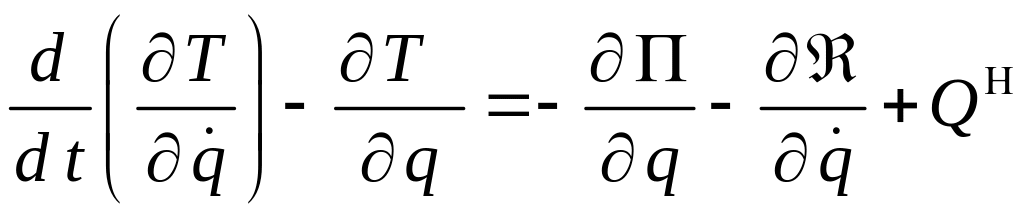где обобщенная неконсервативная сила
определяется выражением
,
а
,
,
— амплитуда, частота и фаза возмущающей
силы.