Потенциальная энергия системы
Потенциальная энергия системы с степенями свободы в общем случае является функцией обобщённых координат
.
Рассмотрим только малые смещения системы из положения равновесия. В этом случае обобщённые координаты , отсчитываемые от равновесного положения, можно рассматривать как величины первого порядка малости.
В положении равновесия системы
потенциальную энергию можно принять
равной нулю
.
Удерживая в разложении потенциальной
энергии
в ряд Маклорена только члены второго
порядка малости, получаем
.
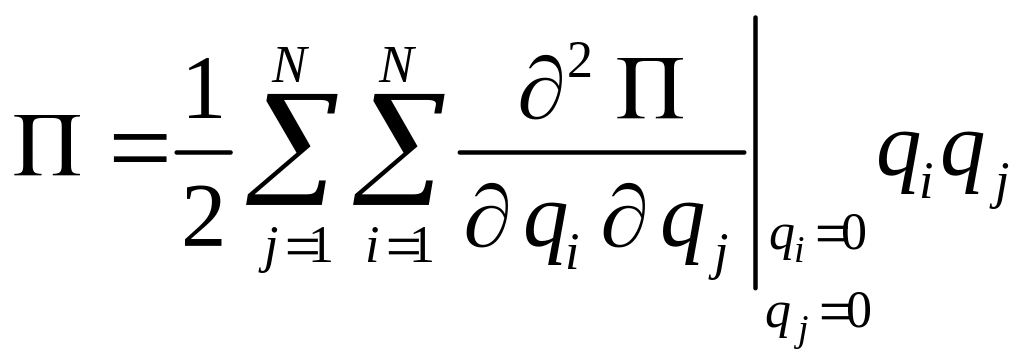Обозначим
,
;
,
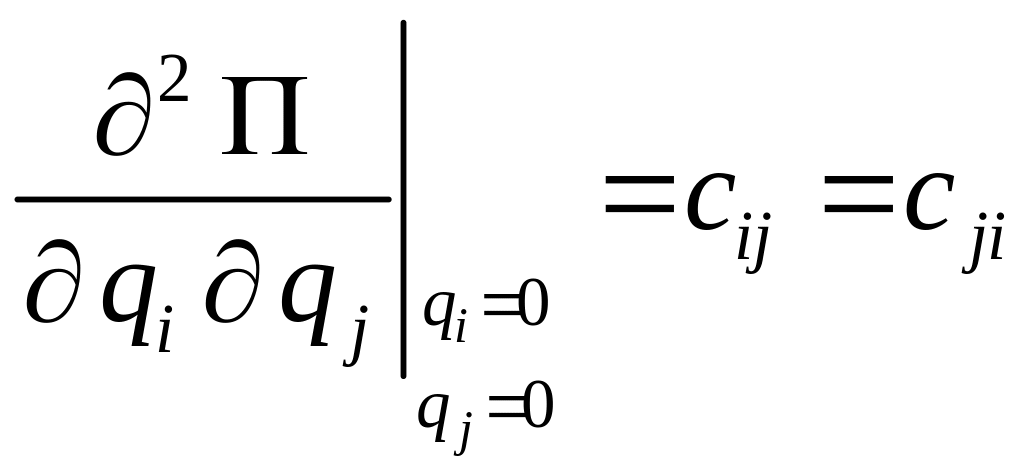где постоянные
имеют название коэффициентов жёсткости.
Таким образом, приближённое выражение
для потенциальной энергии системы
окончательно принимает вид квадратичной
функции от обобщенных координат
:
.
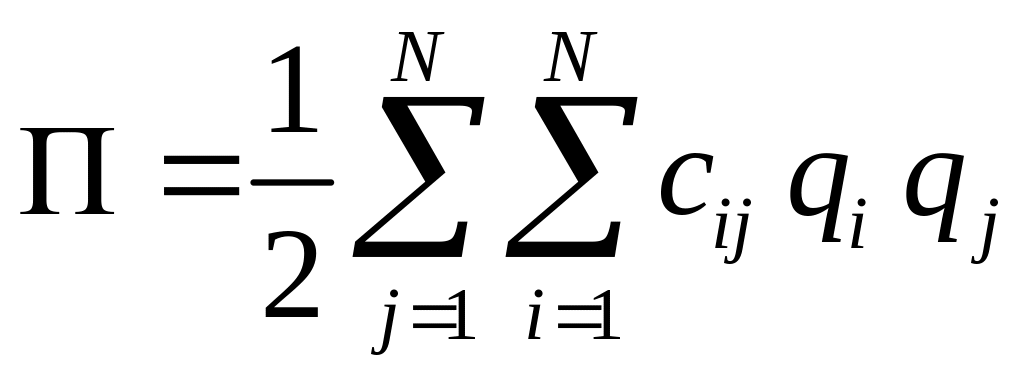Для систем с одной степенью свободы потенциальная энергия вычисляется, следовательно, по формуле:
.
Кинетическая энергия системы
Кинетическая энергия — однородная квадратичная функция обобщённых скоростей с коэффициентами, являющимися функциями обобщённых координат
,
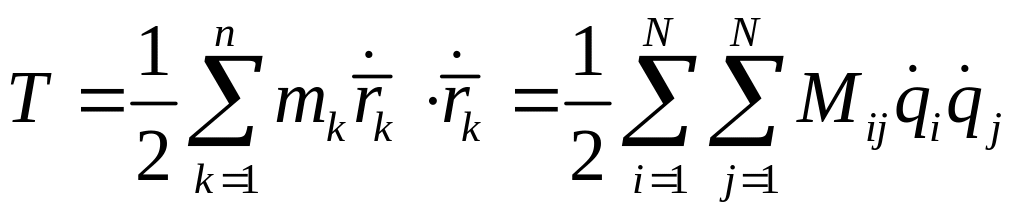где
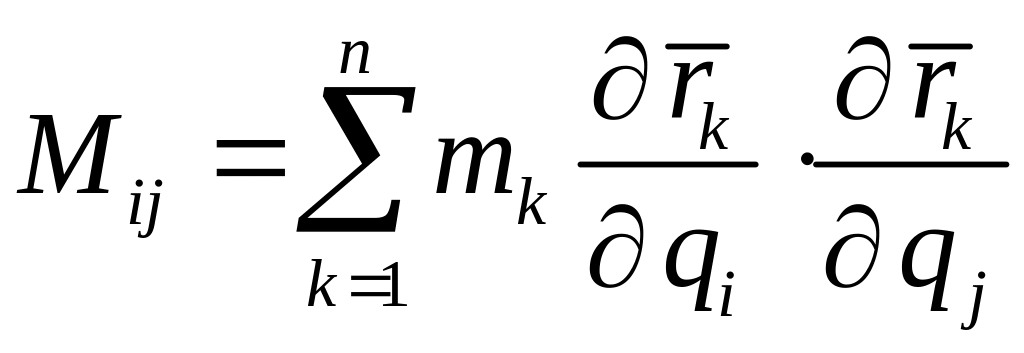— симметричная матрица коэффициентов
.
Так как рассматриваются малые колебания
системы, то ограничимся в разложении
коэффициентов в ряд Маклорена только
первыми постоянными членами, которые
обозначим так:
.
Кинетическая энергия системы приближённо представится в форме:
,
где
— симметричные коэффициенты инерции.
Отсюда для системы с одной степенью свободы
.
Диссипативная функция Рэлея
Пусть на любую точку системы, имеющую степеней свободы, действует сила сопротивления пропорциональная первой степени скорости
,
где
— коэффициент сопротивления.
Силе сопротивления
сопоставляется диссипативная функция
Рэлея
,
характеризующая быстроту рассеивания
(диссипации) энергии системы
,
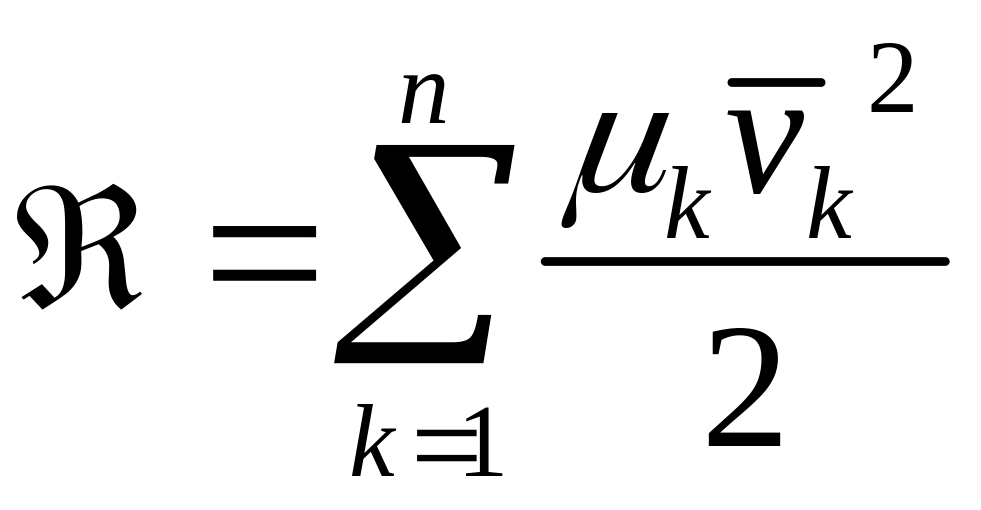которую при стационарных связях
можно представить следующим образом:
,
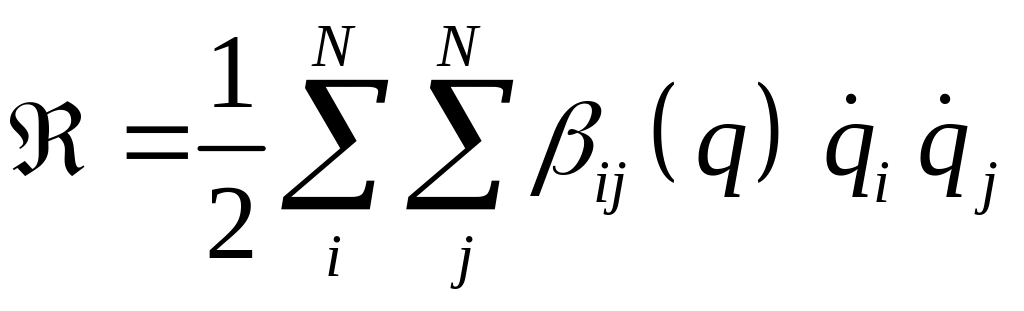где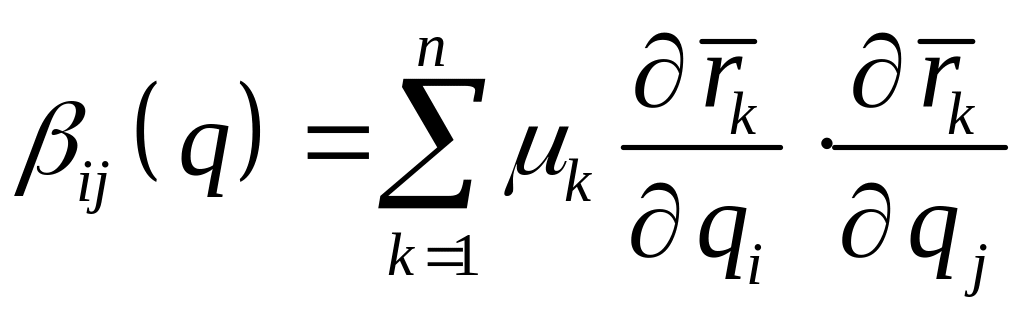
.
Для системы с конечным числом степеней свободы, ограничиваясь в разложении коэффициентов в ряд Маклорена только первыми членами, получим выражение функции рассеивания Рэлея в виде однородной положительной квадратичной функции обобщённых скоростей
,
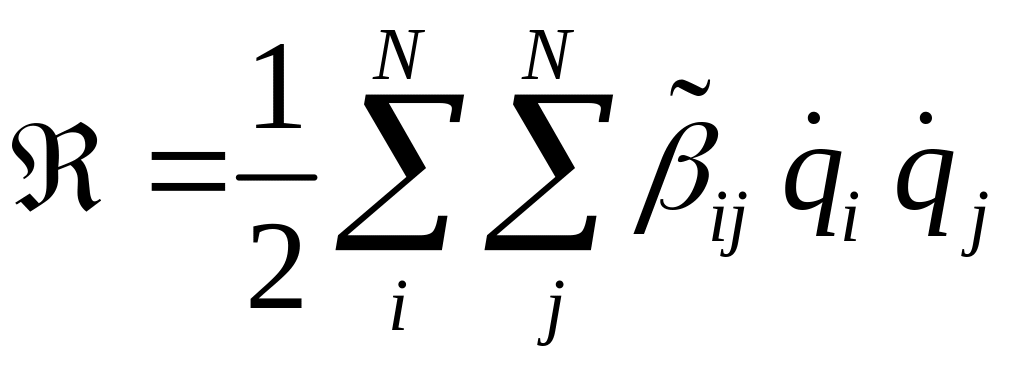где
— постоянные, называемые коэффициентами
диссипации или приведёнными коэффициентами
сопротивления.
Отсюда для системы с одной степенью свободы
.
Уравнение Лагранжа II рода
Уравнение Лагранжа II рода для механической системы со стационарными голономными связями в общем случае неконсервативных (не потенциальных) сил запишется в виде
,
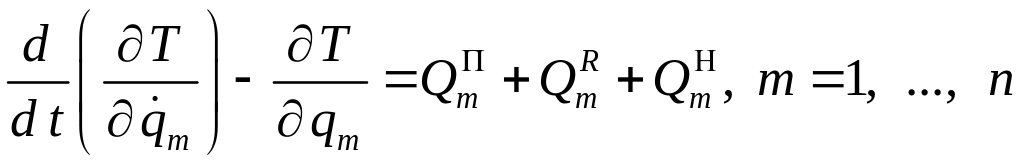где
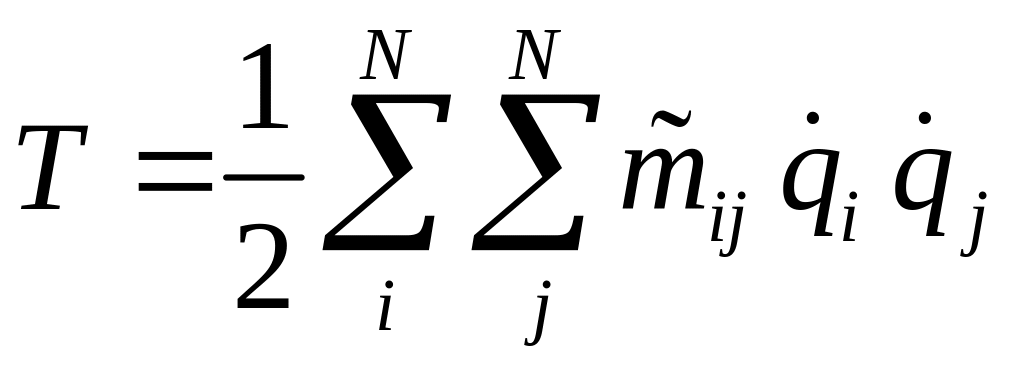— кинетическая энергия системы,
,
,
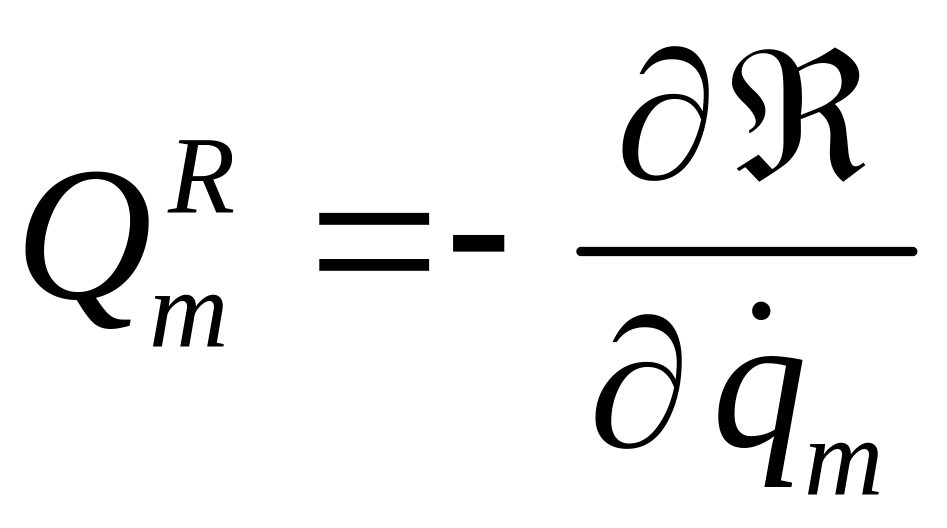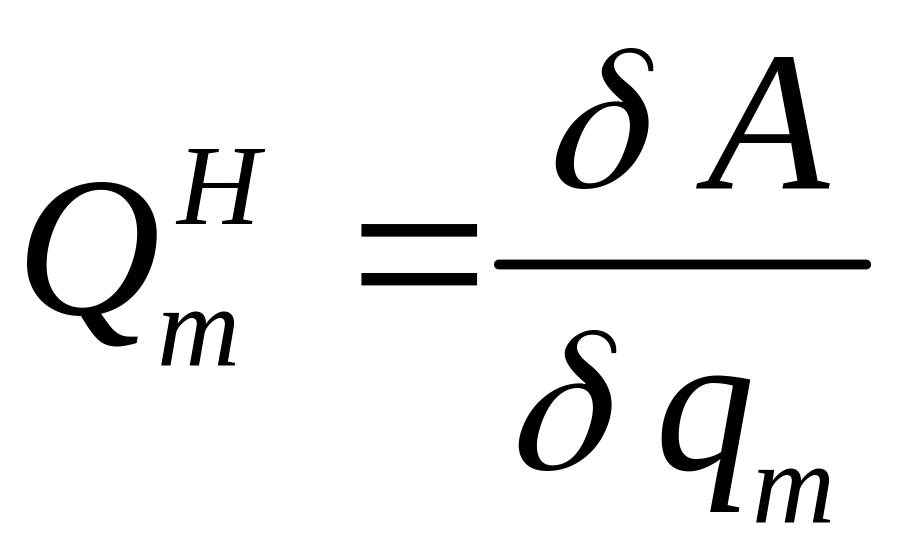— обобщенные потенциальные силы,
обобщенные силы сопротивления и
обобщенные неконсервативные силы
соответственно.
Свободные колебания системы
Рассмотрим движение голономной
механической системы с одной степенью
свободы под действием упругой силы
,
обладающей потенциалом. Положение
системы определяется одной обобщённой
координатой
,
которую будем отсчитывать от равновесного
состояния. Тогда движение системы будет
описываться одним уравнением Лагранжа
II рода:
Подставляя значения кинетической и потенциальной энергии в уравнение Лагранжа, получим дифференциальное уравнение свободных колебаний системы.
,
где
— частота свободных колебаний
механической системы.
Решение этого уравнения можно записать в виде
или
,
где
— константы, определяемые из начальных
условий:
,
или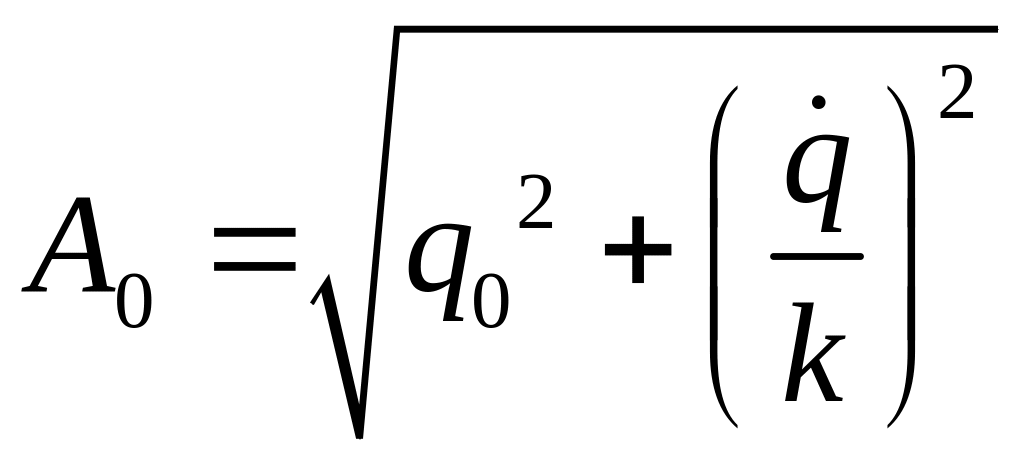
,
.
—
начальное положение и начальная
скорость.
Типичный график движения механической
системы, определяемый данным уравнением,
изображен на рис. 3. 9. Коэффициенты
интегрирования
,
имеют вполне определенный механический
смысл (см. рис. 3. 9):
— амплитуда свободных колебаний,
—
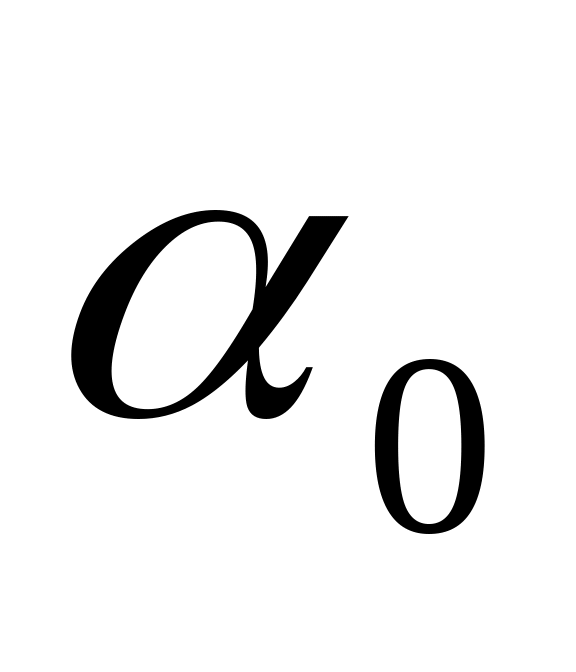начальнаяфаза колебаний.